Inférence bayésienne
En s’appuyant sur le théorème de Bayes, l’inférence bayésienne permet de structurer et mathématiser le raisonnement inductif.
Le raisonnement inductif vise à déduire des faits généraux à partir d’observations ponctuelles, à dévoiler le tableau complet sans n’en avoir vu que des morceaux.
Contrairement au raisonnement déductif dont la conclusion est nécessairement vraie, le raisonnement inductif est, lui, probabiliste et peut donc très bien aboutir à des conclusions fausses. Le logicien anglais Russel prend l’exemple du poulet qui a appris à associer la main qui le nourrit à quelque chose de bénéfique jusqu’au jour où cette même main vient lui tordre le cou. Il s’agit avant tout d’un pari… Parfois perdant.

Malgré son imperfection logique, le raisonnement inductif est partout. Les sciences naturelles se sont en grande partie construites sur lui en proposant des règles extrapolées depuis des résultats d’expériences. On le trouve aussi au cœur des tribunaux (les preuves et témoins sont autant de points de données partiels utilisés pour établir la “vérité”). Et c’est encore lui qui se cache derrière tout diagnostic médical (les indices que sont les symptômes ou les résultats de tests permettent d’inférer l’état du patient).
La recherche en neuroscience va même jusqu’à supposer que nos cerveaux ont une structure biologique adaptée à ce type de raisonnement. Comme le poulet de Russel, notre cerveau semble tirer instinctivement des conclusions des régularités rencontrées. Une étude parue dans Science en 20121 l’illustre bien en montrant que des bébés de 8 mois regardent plus longtemps une boite remplie de boules blanches et rouges lorsqu’on dévoile son contenu si le mélange ne semble pas correspondre à celui inféré à partir d’un échantillon de boules sorties préalablement de la boite !

L’inférence bayésienne est considérée par des chercheurs en neuroscience comme le processus même du traitement de l’information par le cerveau2. Le psychologue spécialisé en neuropsychologie Stanislas Dehaene le présente ainsi dans ses leçons au Collège de France :
Un vaste courant récent des sciences cognitives s’appuie sur la théorie mathématique de l’inférence bayésienne pour modéliser une très grande diversité de phénomènes psychologiques : perception, inférence statistique, prise de décision, apprentissage, traitement du langage… La rapidité avec laquelle cette théorie envahit et unifie divers domaines de la cognition, la simplicité de ses fondements axiomatiques, et la profondeur de ses conclusions justifient de parler d’une véritable « révolution bayésienne » en sciences cognitives.
Pour résumer, la théorie bayésienne fournit un modèle mathématique de la manière optimale de mener un raisonnement plausible en présence d’incertitudes. Dès la naissance, le bébé semble doté de compétences pour ce type de raisonnement probabiliste. L’inférence bayésienne rend également bien compte des processus de perception : étant donné des entrées ambigües, le cerveau en reconstruit l’interprétation la plus probable. La règle de Bayes indique comment combiner, de façon optimale, les a priori issus de notre évolution ou de notre mémoire avec les données reçues du monde extérieur. En cela, elle offre une nouvelle vision de l’apprentissage qui dépasse le dilemme classique entre théories empiristes et nativistes. Enfin, de nombreuses décisions humaines semblent résulter d’une approximation de la règle bayésienne d’accumulation d’évidence, combinée à une estimation de la valeur attendue des conséquences de nos choix.
Dans la mesure où les principes de l’inférence bayésienne sont ainsi partagés par de multiples domaines de la cognition, il se pourrait que l’architecture du cortex ait évolué pour approximer ce type de calcul probabiliste à grande vitesse, et de façon massivement parallèle. L’algorithme utilisé pourrait expliquer non seulement l’organisation du cortex en couches, mais aussi la manière dont notre cerveau anticipe sur le monde extérieur (codage prédictif) et dont il répond à la nouveauté (propagation des signaux d’erreur).
Digression sur le raisonnement avec une autre vidéo d’Hygiéne Mentale.
Bibliothécaire vs agriculteur
On trouve dans le livre “Système 1 / Système 2. Les deux vitesses de la pensée” du prix Nobel d’économie Daniel Kahneman une expérience illustrant ce que peut nous apporter une meilleur familiarité avec le bayésianisme.
L’expérience consistait à présenter à un amphi le portrait suivant :
Steve est très timide et réservé, toujours prêt à rendre service, mais sans vraiment s'intéresser aux gens ou à la réalité. Personnalité docile et méticuleuse, il a besoin d'ordre et de structure, et se passionne pour les détails.
Puis on demande à l’audience si Steve est plus susceptible d’être bibliothécaire ou agriculteur.

Une large majorité répond alors bibliothécaire tant le portrait est proche du stéréotype associé à cette profession.
Et c’était aussi le cas de ChatGPT 3.5 au départ (rappelons qu’il ne s’agit pas d’une IA qui raisonne mais d’une IA produisant un discours visant à satisfaire l’utilisateur) :

Mais sachant qu’aux Etats-Unis, où l’étude a été menée, il y a au moins 20 fois plus d’agriculteurs que de bibliothécaires, les chances que Steve soit bibliothécaire sont minces.
Un raisonnement bayésien nous aurait prémuni d’une conclusion trop hâtive sur la profession de Steve. Il consiste non pas à déduire une probabilité d’une information donnée mais à mettre à jour une probabilité a priori à partir de cette information.
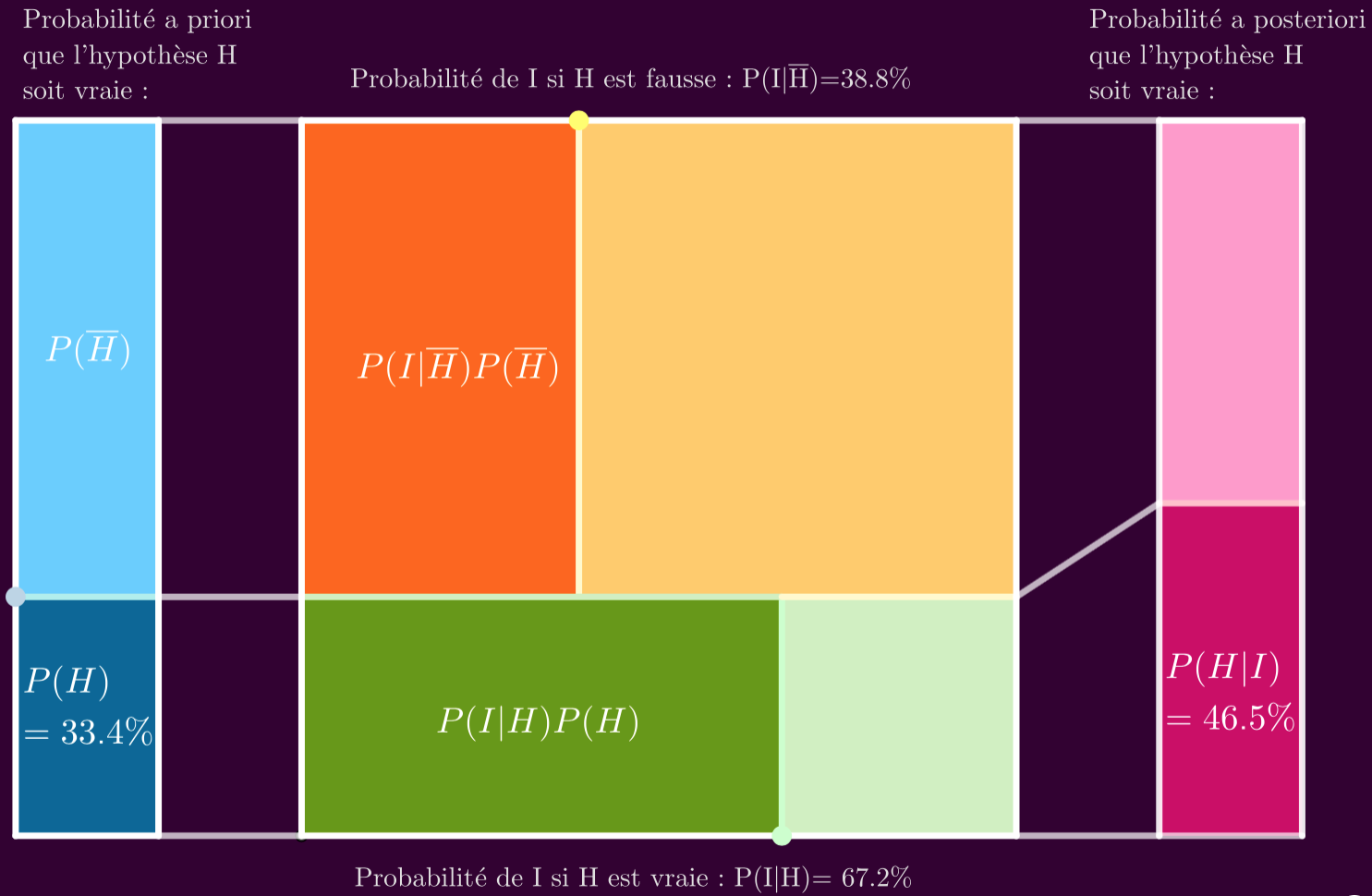
La probabilité a priori de l’hypothèse $H$ est $\textcolor{#0076BA}{P(H)}$.
Ici, l’hypothèse est que Steve est bibliothécaire et la probabilité a priori vaut 4,8% $\left(\frac{1}{20+1}\right)$.
La probabilité a priori de l’hypothèse contraire $\overline{H}$ vaut $\textcolor{#56C1FF}{P(\overline{H})}=1-\textcolor{#0076BA}{P(H)}$.
Ici, cela correspond à un Steve agriculteur puisqu’on suppose qu’il est soit bibliothécaire, soit agriculteur. La probabilité a priori d’un Steve agriculteur vaut 95,2%.
Le portrait de Steve est l’information nouvelle apportée $I$, elle modifie la plausibilité que Steve soit bibliothécaire tel un curseur qui va tirer la probabilité dans un sens ou dans l’autre. La probabilité de l’information $I$ est notée $\textcolor{#1DB100}{P(I)}$.
La probabilité a posteriori correspond alors à la probabilité de $H$ sachant $I$, qu’on note $\textcolor{#CB297B}{P(H|I)}$ (que devient la probabilité de $H$ une fois qu’on a connaissance de l’information $I$).
C’est le théorème de Bayes qui va nous permettre de mettre à jour la probabilité a priori pour obtenir la probabilité a posteriori :
-
$\textcolor{#FF644E}{P(I|H)}$ est la probabilité d’avoir $I$ si $H$ est vraie (probabilité que Steve corresponde à la description s’il est bibliothécaire).
-
$\textcolor{#00A89D}{P(I|\overline{H})}$ est la probabilité d’avoir $I$ si $H$ est fausse (probabilité que Steve corresponde à la description s’il est agriculteur).
Ces deux probabilités ne sont pas connues, mais on peut les estimer !
L’illustration ci-dessous permet de se rendre compte que le théorème de Bayes est finalement assez trivial :
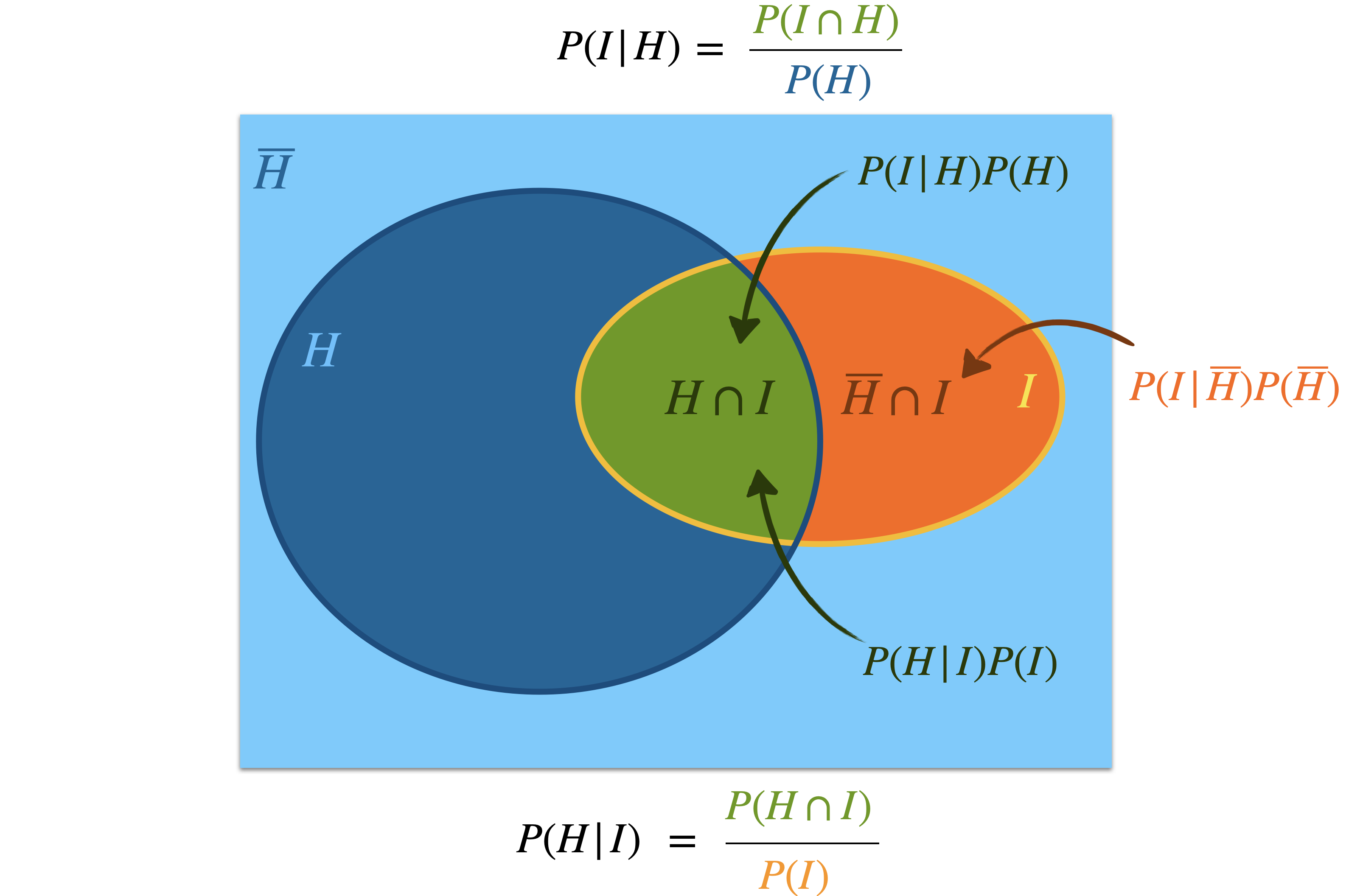
Et encore plus trivial avec le plus grand effort pédagogique fait ci-dessous :
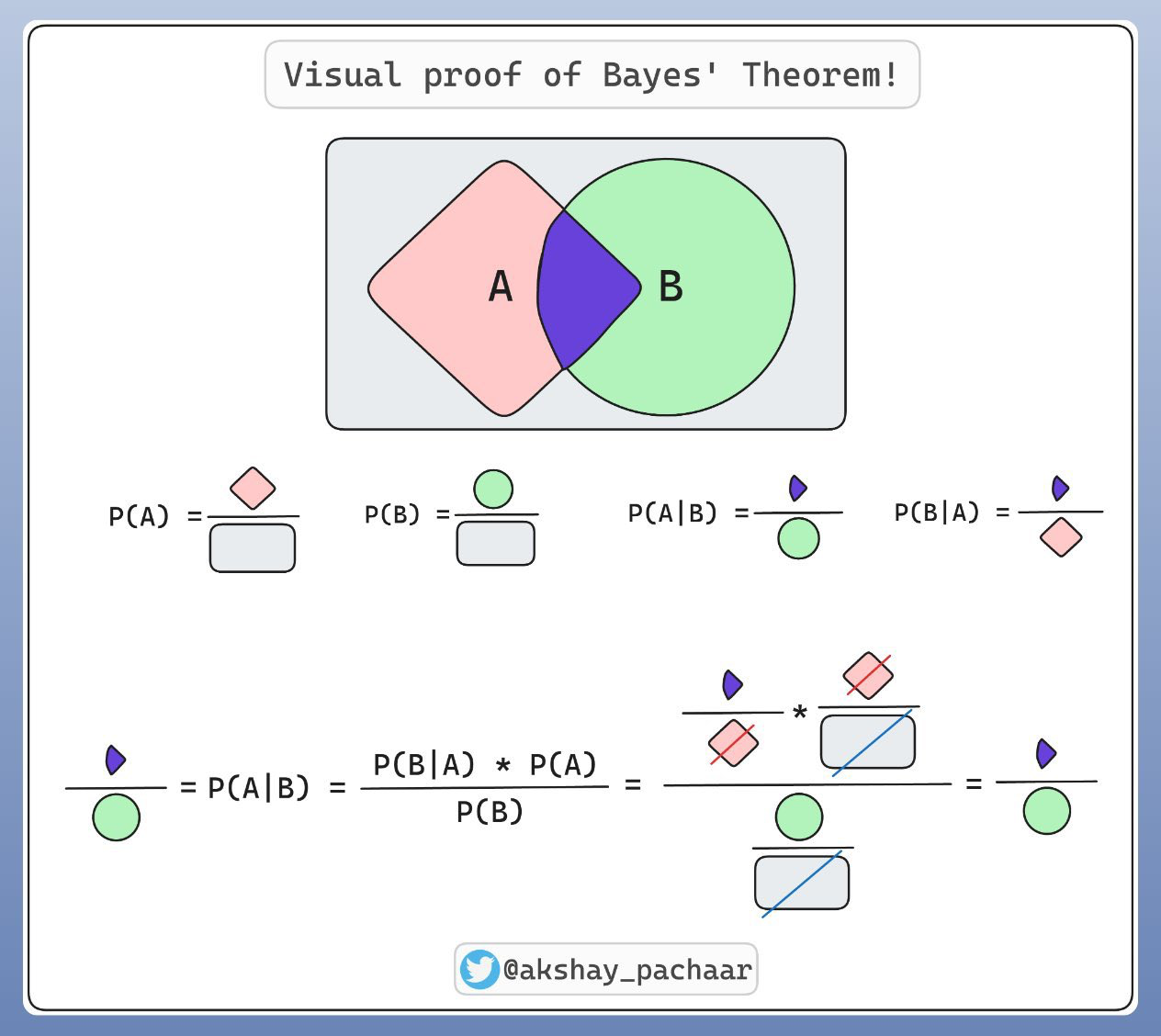
On peut utiliser la représentation graphique décrite dans la vidéo d’introduction pour nous aider à faire les calculs en fonction de nos estimations. C’est ce qui est fait dans l’appliquette Geogebra ci-dessous (cliquer pour l’ouvrir).
En supposant que le portrait corresponde à 40% des bibliothécaires et à 5% des agriculteurs, que vaut la probabilité a posteriori que Steve soit bibliothécaire ?
La probabilté que le portrait corresponde à un bibliothécaire devrait être combien de fois supérieure à celle qu’il corresponde à un agriculteur pour faire basculer la probabilité a posteriori que Steve soit bibliothécaire au-delà de 50% ? Comparez au ratio bibliothécaires sur agriculteurs.
Moralité, le portrait correspond probablement plus à un agriculteur !
Les fréquentistes et les bayésiens interprètent les probabilités différemment.
Pour les fréquentistes, une probabilité est la limite vers laquelle tendrait une fréquence mesurée sur un échantillon lorsqu’on fait tendre la taille de l’échantillon vers l’infini.
Pour les bayésiens, une probabilité mesure un degré de conviction qui est mis à jour à chaque nouvelle information obtenue.
Autre célèbre exemple de portrait tiré du même livre de Kahneman (et toujours avec ChatGPT comme cobaye) :
je pleure pic.twitter.com/d9qL7qcp2I
— Dr. Juliette (@FerryDanini) February 12, 2023
Le paradoxe des deux enfants
Un couple a deux enfants. On nous informe que l’un des deux est une fille. Quelle est la probabilté que les deux enfants soient des filles ?

Utilisez le théorème de Bayes pour répondre en précisant d’abord $H$ et $I$, puis en déterminant les différentes probabilités $P(H)$, $P(I|H)$ et $P(I)$.
Vérifier votre résultat en complétant le code python suivant afin qu’il simule une expérience sur 100000 couples de deux enfants.
Un couple a deux enfants. On apperçoit une fille dans le jardin. Quelle est la probabilté que les deux enfants soient des filles ?
La réponse change-t-elle ?
Correction (cliquer pour afficher)
Oui : dans l'hypothèse où il y a deux filles (1 chance sur 4), il y a 100% de chance de voir une fille dans le jardin. Et dans l'hypothèse où il n'y a pas deux filles ($\bar{H}=3/4$), il y a 1 chance sur 3 de voir une fille dans le jardin (il faut à la fois que les parents aient un garçon et une fille, 2 chance sur 3, et il faut que cela soit la fille dans le jardin, 1 chance sur 2). On a donc $P(H|I)=\frac{1\times 1/4}{1\times 1/4 + 1/3\times 3/4}=\frac{1}{2}$.
Comment modifier le code pour qu’il corresponde à cette situation ?
Correction (cliquer pour afficher)
from random import randint vufillejardin = 0 deuxfilles = 0 n = 100000 enfants = [None,None] for i in range(n): enfants[0] = randint(0,1) enfants[1] = randint(0,1) if enfants[randint(0,1)] == 1: # on voit une fille dans le jardin (on tire au sort l'enfant) vufillejardin += 1 if enfants[0] == enfants[1]: # deux filles deuxfilles += 1 P = deuxfilles/vufillejardin*100 print(f"Probabilité qe les parents aient deux filles sachant qu'on a vu une fille dans le jardin : {P:.1f}%")
la probabilité a priori d’avoir deux filles vaut 1/4.
L’information apportée tire cette probabilité vers le haut.
Elle tire plus dans le second cas que dans le premier, car l’information est plus précise ; un tirage a été fait.
Dans le premier cas, l’information supplémentaire laisse trois possibilités équiprobables (on sait seulement que le couple ne peut pas avoir deux garçons), alors que dans le second, il n’y en a plus que deux (l’autre enfant est soit une fille, soit un garçon) !
Problème de Monty Hall
Dans un ancien jeu télévisé américain, présenté par Monty Hall, un candidat devait choisir une porte parmi trois. Derrière l’une d’elles se cache une voiture et derrière les deux autres une chèvre.
Après que le candidat ait indiqué son choix, Monty ouvre une des deux autres portes derrière laquelle il sait que se trouve une chèvre (s’il y a une chèvre derrière les deux portes non choisies, il en choisit une au hasard).
Il demande ensuite au candidat s’il veut garder sa porte ou s’il veut choisir l’autre porte.
Doit-il changer de porte ?
Supposons que vous ayez préalablement choisi la porte 1 et que Monty ouvre la porte 2. Montrez en utilisant le théorème de Bayes que le candidat a intérêt à changer de porte.
Pour raisonner, on va prendre pour hypothèse $H$ “il y a une voiture derrière la porte 3” et pour information $I$ : “Monty ouvre la porte 2”.
Correction (cliquer pour afficher)

L’argument de l’Apocalypse
Le philosophe Nick Bolstrom présente sa version du “Doomsday Argument” à peu près ainsi :
1re étape :
Imaginez un univers constitué de 100 boites habitées chacune par un humain.
L’extérieur des boites est peint en bleu pour 90 d’entre elles et en rouge pour les 10 autres.
Chaque personne connaît la situation et on leur demande de deviner la couleur de leur boite.
Que répondez-vous ?
Correction (cliquer pour afficher)
Si vous supposez qu'il y a 90% de chance que votre boite soit bleue, vous êtes SSA (self-sampling assumption) dans la terminologie de Bostrom. Et si vous pensez plutôt qu'il n'y a que 50% de chance qu'elle soit bleue, vous échappez à la conclusion du Doomsday.
2e étape :
On modifie un peu l’expérience en remplaçant la couleur des boites par une numérotation entre 1 et 100 (le numéro est, là encore, peint à l’extérieur).
Maintenant, un dieu bizarre lance une pièce. Si ça tombe sur face, il crée une personne dans chaque boite et si ça tombe sur pile, il ne crée des personnes que dans les boites 1 à 10.
Vous vous retrouvez dans une de ces boites et on vous demande s’il y a 10 ou 100 personnes dans l’univers.
N’ayant pas d’information supplémentaire, que répondez-vous ?
Et si on vous demande d’estimer la probabilité que le numéro de votre pièce soit entre 1 et 10 selon chacune des deux possibilités pour le pile ou face ?
Supposons maintenant que vous sortiez de votre boite pour découvrir que son numéro est le 7.
On vous demande alors d’estimer la probabilité que la pièce soit tombée sur pile maintenant que vous connaissez le numéro de votre boite.
Correction (cliquer pour afficher)
$$ \color{#006C65} \begin{aligned} P(\text{Pile}|7)&=\frac{P(7|\text{Pile})P(\text{pile})}{P(7|\text{Pile})P(\text{pile})+P(7|\text{face})P(\text{face})}\\ &=\frac{1/10\times 1/2}{1/10\times 1/2 + 1/100\times 1/2}\\ &=\frac{10}{11}\\ &=91\% \end{aligned} $$
3e étape :
On transpose ces résultats à la situation actuelle sur Terre.
Posons les deux hypothèses rivales suivantes :
- apocalypes précoce : l’humanité va s’éteindre dans le prochain siècle et la quantité totale d’humain ayant existé sera d’environ 200 milliards.
- apocalypse tardive : l’humanité va survivre le prochain siècle et coloniser la galaxie. Le nombre total d’humain ayant existé s’élèvera à 200 mille milliards.
Quelle probabilité a priori attribuez-vous à chacun de ces scénarios ?
Vous n’êtes pas loin d’être l’humain n°100 milliards (en terme d’ordre de naissance).
Comme le théorème de Bayes va-t-il faire glisser les probabilités attribuées à chacun des scénarios sachant cela (faire le parallèle avec l’univers des boites numérotées).
Commentaire (cliquer pour afficher)
On peut échapper à cette conclusion sinistre en rejetant SSA. On peut en effet considérer qu'il y a plus de chance qu'il y ait 100 personnes que 10 car le fait que j'existe devient alors plus probable.
Sans connaître le numéro de la boite, on peut donc penser qu'il y a 10 fois plus de chances que dieu ait tiré face. Cela rééquilibre a posteriori les deux hypothèses car maintenant, $P(\text{Pile}|7)$ vaut 1/2 et de même, les deux scénarios d'apocalypse retrouvent leurs probabilités a priori.

Nick Bostrom a aussi développé des arguments semblables sur la probabilité que l’on vive dans une simulation.
Bayes et cote
Le raisonnement de la question 2 suggère de réexprimer le théorème de Bayes en terme de cotes, ce qui va permettre de simplifier à la fois son calcul et son interprétation.
La cote d’un événement (odds en anglais) est le ratio de la probabilité que l’événement se produise par la probabilité qu’il ne se produise pas. On l’exprime en général comme une paire de nombres (le numérateur et le dénominateur).
Par exemple, si un évènement a une probabilité de 5% de se produire, il a donc aussi une probabilité de 95% de ne pas se produire et sa cote est alors de 5 contre 95 (ou 1 contre 19 qu’on peut aussi noter $1:19$).
Si un pari consiste à obtenir un 5 ou un 6 au dé, que vaut alors sa cote ?
À quelle cote correspond une probabilité de 50% ?
L’utilisation des cotes est très commune pour les paris sportifs en Angleterre.
Théorème de Bayes exprimé en termes de cote :
Le facteur de Bayes mesure le mérite relatif des deux hypothèses $H$ et $\bar{H}$, le rapport de leurs vraisemblances.
Vérifions avec Steve :
La cote de $H$ correspond au ratio bibliothécaires/agriculteurs (soit 1/20) et le facteur de Bayes correspond à combien de fois le portrait $I$ correspond plus à un bibliothécaire qu’à un agriculteur. Si le facteur de Bayes vaut 20, on trouve une cote de 1 pour la cote a posteriori, ce qui correspond bien à une probabilité de 50% que Steve soit bibliothécaire.
Reprenez la première questions du paradoxe des deux filles en utilisant les cotes.
Inférence bayésienne et diagnostic médical
Le psychologue Gerd Gigerenzer présente le problème suivant dans un séminaire de statistique à des gynécologues en activité :
Une femme de 50 ans sans symptôme passe une mammographie de routine. L'examen se révèle positif. Alarmée, elle veut savoir avec quelle certitude cela implique qu'elle a un cancer du sein.
À part le résultat du test, vous ne savez rien sur cette femme.
La prévalence des cancers du sein est de 1% chez les femmes de cet âge.
La sensibilité du test est de 90%.
Et sa spécificité est de 91%.
Parmi les femmes dont le test est positif, combien sont atteintes d'un cancer du sein ?
A : 9 sur 10 ; B : 8 sur 10 ; C : 1 sur 10 ; D : 1 sur 100
Un peu de vocabulaire :
- La sensibilité d’un test mesure sa capacité à donner un résultat positif lorsqu’une hypothèse est vérifiée = capacité à détecter un maximum de malades (avoir le moins possible de faux négatifs).
- La spécificité d’un test mesure sa capacité à donner une résultat négatif lorsque l’hypothèse n’est pas vérifiée = capacité à ne détecter que les malades (avoir le moins possible de faux positifs).
En notant VP et FP les vrais et les faux positifs, et VN et FN les vrais et faux négatifs, on a :
| Malade | Non malade | |
|---|---|---|
| Test positif | VP | FP |
| Test négatif | FN | VN |
-
sensibilité $=\frac{VP}{VP+FN}$
-
spécificité $=\frac{VN}{VN+FP}$

En utilisant le code couleur du schéma précédent, un test sera d’autant plus sensible que l’ensemble des malades (hachuré rouge) ne déborde pas de l’ensemble des tests positifs (hachuré bleu). La sensibilité est en effet donnée par la proportion entre l’aire à la fois hachurée rouge et bleue (les VP) sur toute l’aire hachurée rouge (les malades).
Et la spécificité correspond à la proportion d’aire verte seule (les non malades avec un test négatifs, VN) sur toute l’aire verte (verte seule + verte hachurée bleue, alias l’ensemble des non malades).
En bon bayésien, il ne faut pas considérer qu’un test détermine si on a une maladie, ni même qu’il détermine les chances d’avoir une maladie.
Tout ce qu’il fait, c’est mettre à jour les chances d’avoir une maladie !
Que vaut le facteur de Bayes dans cet exemple ?
Réponse (cliquer pour afficher)
$\displaystyle \frac{P(+|\text{Cancer})}{P(+|\overline{\text{Cancer}})}=\frac{\text{probabilité de vrais positifs}}{\text{probabilité de faux positifs}}=\frac{\text{sensibilité}}{\text{1-spécificité}} $
Le théorème de Bayes version cote devient donc :
$\displaystyle cote(\text{cancer}|+)=\frac{\text{sensibilité}}{\text{1-spécificité}}\times cote(\text{cancer}) $
Quelle est la bonne réponse (les cotes permettent de l’estimer facilement) ?
Plus de la moitié des docteurs présents ont choisi la réponse A, ce qui est très à côté de la plaque, et seulement 1 sur 5 ont choisi la bonne réponse…
Changeons la prévalence à 10 % :
| prévalence | 10% |
|---|---|
| sensibilité | 90% |
| spécificité | 91% |
Que devient la probabilité d’avoir un cancer en cas de test positif ?
Passons-la maintenant à 0,1 % :
| prévalence | 0,1% |
|---|---|
| sensibilité | 90% |
| spécificité | 91% |
Que vaut $P(cancer|+)$ maintenant ?
Augmentons la spécificité à 99 % et reprenant une prévalence de 1 %.
| prévalence | 1% |
|---|---|
| sensibilité | 90% |
| spécificité | 99% |
Que devient la probabilité ?
Et si le test est négatif ?
Reprendre les données de départ et trouvez la probabilité de ne pas avoir de cancer si on a été testé négatif.
Et si on passe un second test négatif ?
Moustiques
Trois maladies virales peuvent être transmises par les moustiques :
- dengue
- chikungunya
- zika
Elles provoquent des symptômes qui peuvent être assez proches, ce qui les rend difficiles à différencier directement.

Ici on s’intéresse à la mise en place d’une aide statistique au diagnostic. Pour cela, on va s’appuyer sur des données obtenues chez des personnes dont le diagnostic a pu être certifié par des examens biologiques. Pour simplifier, on supposera que ces caractères apparaissent indépendamment chez les personnes infectées.
| symptômes | Dengue | Chikungunya | Zika |
|---|---|---|---|
| Fièvre | 95% | 75% | 75% |
| Courbatures | 75% | 95% | 50% |
| Douleurs oculaires | 50% | 25% | 50% |
| Déficit globules blancs | 50% | 50% | 25% |
| Hémorragie | 25% | 5% | 5% |
À partir de ces données, on veut déterminer les probabilités de chaque maladie selon les symptômes présentés et dans des conditions différentes.
La forme du théorème de Bayes la plus pratique est dans ce cas :
Vous êtes internes au service de maladies infectieuses du CHU de Limoges et une personne se présente avec à la fois de la fièvre, pas de courbatures et des douleurs oculaires. La personne revient d’un pays dans lequel aucune des trois maladies n’est épidémique. On considère donc a priori que les trois maladies sont équiprobables.
Calculer la probabilité que la personne présente ces 3 symptômes ensemble pour chacune des maladies $P(\text{symptômes}|\text{maladie})$.
Calculer la probabilité d’avoir ces symptômes quelle que soit la maladie $P(\text{symptômes})$
aide : $P(\text{symptômes})=\sum_{\text{maladie}}P(\text{symptômes}|\text{maladie})\times P(\text{maladie})$Quelles sont les probabilités a posteriori de chaque maladie si cette personne présente ces symptômes ? Quel est selon vous le diagnostic le plus probable dans ce cas ?
Si vous apprenez maintenant qu’en fait la personne revient d’un pays dans lequel sévit une épidémie de Chikungunya. A priori, il y a 90 % de chances qu’elle ait été infectée par le Chikungunya et 5 % par chacune des deux autres maladies. Quel est le diagnostic le plus probable dans ce cas ?
Un des premiers programmes de filtrage bayésien du courrier électronique était le programme iFile de Jason Rennie, publié en 1996.
Le principe, analogue à celui du diagnostic médical, repose sur le fait que les mots du dictionnaire ont des probabilités différentes d’apparaître dans les spams et dans les courriers légitimes.
Le filtre de détection des spams ne connaît pas à l’avance les probabilités d’apparition de ces mots, c’est pourquoi il lui faut une phase d’apprentissage pour les évaluer. Cette phase d’apprentissage est analogue à la phase de calibrage du test médical étudié ci-dessus.
L’apprentissage se fait à partir de l’observation du comportement des utilisateurs, qui doivent indiquer manuellement si un message est un spam ou non. Pour chaque mot de chaque message « appris », le filtre ajustera les probabilités de rencontrer ce mot dans un spam ou dans un courrier légitime et le stockera dans sa base de données.
On note $P(M|S)$ la probabilité qu’un spam contienne le mot $M$ et $P(M|\overline{S})$ la probabilité qu’un courrier légitime contienne le mot $M$. Ces deux probabilités sont estimées au cours de la phase d’apprentissage, tout comme la probabilité $P(S)$ qu’un message quelconque soit un spam (analogue à la prévalence $P(\text{maladie})$ dans le test médical).
Une fois ces valeurs déterminées, la formule de Bayes permet de calculer la probabilité qu’un message donné soit un spam sachant qu’il contient le mot $M$ selon la formule :
$\displaystyle P(S|M)=\frac{P(M\cap S)}{P(M)}=\frac{P(M|S)P(S)}{P(M|S)P(S)+P(M|\bar{S})P(\bar{S})}$
Cette probabilité est comparée à un seuil ; si elle est supérieure au seuil,
le filtre classera ce message dans les spams.
Dans la réalité, on travaille non pas sur un seul mot $M$, mais sur un stock de mots, en faisant l’hypothèse naïve que les mots présents dans un message sont indépendants les uns des autres. Cela est faux dans les langages naturels, où par exemple la probabilité de trouver un adjectif est influencée par celle de trouver un nom. De plus, cette technique
de filtrage, connue sous le nom de filtrage bayésien naïf, ne tient pas compte du sens
des mots, alors qu’il a une incidence sur la présence simultanée de certains mots à l’intérieur du message. Par exemple, la présence du mot « anniversaire » n’est pas indépendante de celle du mot « joyeux ».
-
Alison Gopnik, “Scientific Thinking in Young Children: Theoretical Advances, Empirical Research, and Policy Implications”, Science, 337(6102), 1623–1627 (2012). DOI: 10.1126/science.1223416. ↩︎
-
Hansem Sohn & Devika Narain, “Neural implementations of Bayesian inference”, Current Opinion in Neurobiology, 70, 121–129 (oct. 2021). DOI: 10.1016/j.conb.2021.09.008. ↩︎