Transport de l’électricité
Savoir et savoir faire
Savoir schématiser l’organisation du transport et de la distribution de l’énergie électrique pour une ligne monophasée.
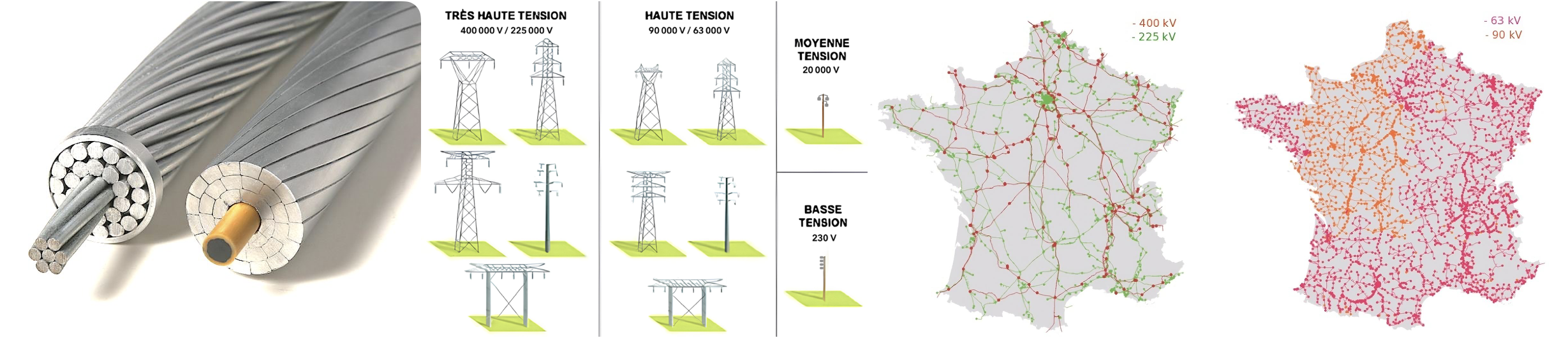
Distinguer et citer les caractéristiques essentielles du réseau de distribution électrique.
Relier qualitativement le facteur de puissance d’un équipement de puissance donnée aux pertes dans les lignes d’alimentation.
Citer les rôles du transformateur (élévation de tension, diminution de tension, isolation galvanique).
Relier qualitativement l’augmentation, pour une charge donnée, de la tension de distribution à la diminution des pertes dans les lignes d’alimentation.
Exploiter des documents mettant en évidence les seuils de dangerosité du courant électrique.
Citer des dispositifs de protection des individus contre les risques du courant électrique : isolation, alimentation en très basse tension et disjoncteur différentiel dans une installation domestique.
Citer des dispositifs de protection des matériels contre les risques du courant électrique : fusible et disjoncteur.
On a vu que la puissance dissipée par effet Joule s’écrit $P_J = RI^2$. Cette formule s’obtient en écrivant que la puissance électrique dissipée par un dipôle ohmique est $P_J=U_R\times I = R\times I\times I$ où on a utilisé la loi d’Ohm aux bornes du dipôle ohmique $U_R = R\times I$.
Pour une puissance transportée $P=UI$ donnée, minimiser les pertes $P_J$ suppose donc de minimiser $I$ (et $R$).
Mais on aurait aussi très bien pu remplacer $I$ par $\frac{U_R}{R}$ dans la formule de la puissance dissipée par effet Joule pour obtenir $P_J=\frac{U_R^2}{R}$. Cela semble alors imposer une conclusion inverse que précédemment ; il faudrait diminuer $U$ et augmenter $R$.
Mais alors, il faut augmenter ou diminuer $U$ ? 🤔
Comme on a bien fait attention de l’indiquer, il s’agit de $U_R$ (la tension aux bornes de la résistance) dans la formule de $P_J$, et non de $U$ (la tension de la ligne électrique) qui est la tension qu’on utilise dans le calcul de la puissance $P=UI$ transportée.
Montrons sur un exemple qu’en utilisant la formule $P_J=\frac{U_R^2}{R}$, on aboutit bien encore à la conclusion qu’il faut augmenter $U$ pour diminuer les pertes.
Imaginons une ligne électrique sous une tension efficace de $\pu{1000 V}$ et traversée par une intensité efficace de $\pu{10 A}$ qui transporte donc une puissance de $\pu{10 kW}$ (on suppose ici pour simplifier que le facteur de puissance vaut 1). Pour un tronçon de câble présentant une résistance de $\pu{1 \Omega}$, la chute de tension $U_R$ vaut $R\times I = \pu{10 V}$, soit 1% de la tension de la ligne. Cela représente une puissance dissipée valant $P_J=\frac{U_R^2}{R}=\pu{100 W}$, 1% de la puissance transportée.
Si on élève la tension d’un facteur 100, on se retrouve avec une intensité divisée par 100 (on transporte toujours la même puissance $U\times I$). La chute de tension $U_R$ vaut alors $\pu{0,1 V}$ et $P_J$ passe à seulement $\frac{0,1^2}{1}=\pu{10 mW}$, donc seulement un millionième de la puissance transportée.
Documents
- 10 règles élémentaires de sécurité
- Document plus complet sur l’électricité et ses dangers
- Article plutôt complet sur le transport de l’électricité
- Activité lignes à haute tension
- TP transformateur
Quiz
Elle est parcourue par un courant d'intensité efficace $\pu{I = 134 A}$.
La puissance dissipée par effet joule est égale à : - [x] $\pu{32 kW}$ - [ ] $\pu{2,4E2 W}$ - [ ] $\pu{59 W}$ ## Pour passer d'une tension de 20 kV à 400 kV, on utilise : - [x] un transformateur élévateur de tension - [ ] un poste de distribution - [ ] un interrupteur à haute tension > https://presentationssite.github.io/tsti/transport/#/7 ## Un transformateur est constitué de $N_1=500$ spires au primaire et $N_2 = 50$ spires au secondaire. - [x] son rapport de transformation $m$ vaut 0,1 - [ ] son rapport de transformation $m$ vaut 10 - [ ] son rapport de transformation $m$ vaut 1 ## On applique au primaire d'un transformateur ayant un $m$ valant 0,02 une tension efficace $U_1=\pu{20 kV}$. - [x] la tension efficace au secondaire vaut 400 V - [ ] la tension efficace au secondaire vaut 230 V - [ ] la tension efficace au secondaire vaut 0,4 V ## Un transformateur fonctionne pour des tensions : - [ ] continues - [x] alternatives - [x] sinusoïdales ## Un fusible de calibre 2 A est installé sur un grille-pain. - [ ] il protège la personne qui utilise le grille-pain - [x] il protège le grille-pain contre une surintensité - [x] il coupe le circuit si l'intensité efficace dépasse 2 A. ## Un disjoncteur différentiel associé à une prise de terre : - [ ] protège les personnes de l'électrisation - [x] protège les personnes de l'électrocution - [ ] coupe le circuit en cas de surintensité ## Dans une salle de bain, la valeur efficace de la tension de sécurité vaut : - [ ] 230 V - [x] 25 V - [ ] 50 V ## Dans une salle de TP, la valeur efficace de la tension de sécurité vaut : - [ ] 230 V - [ ] 25 V - [x] 50 V