Rappels sur les solutions
Pictogrammes
Savoir et savoir faire
coeur
Calculer la masse molaire d’une molécule à partir de celles des atomes qui la constituent.
Calculer une quantité de matière $n$ d’une espèce chimique à partir de la masse $m$ de l’espèce et de sa masse molaire $M$ : $\displaystyle n=\frac{m}{M}$
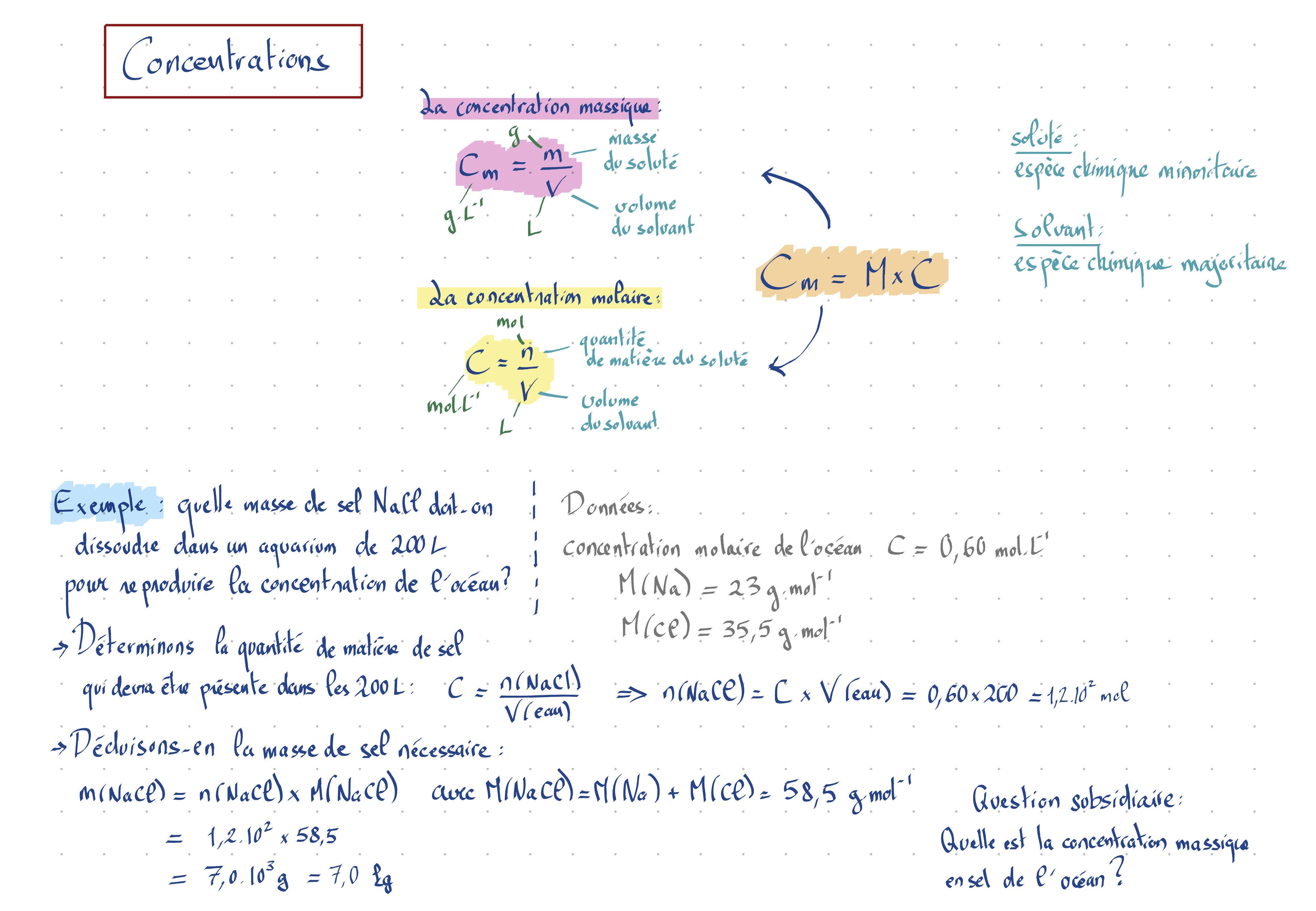
Déterminer une concentration massique $\displaystyle C_m=\frac{m}{V}$ et une concentration molaire $\displaystyle C=\frac{n}{V}$
Déterminer une masse $m$ à partir d’un volume $V$ et d’une masse volumique $\rho$ : $m=\rho\times V$
Déterminer une masse $m$ à partir d’un volume $V$ et d’une concentration massique $C_m$ : $m=C_m\times V$
Déterminer une quantité de matière $n$ à partir d’un volume $V$ et d’une concentration molaire $C$ : $n=C\times V$
Donner le protocole d’une dissolution.
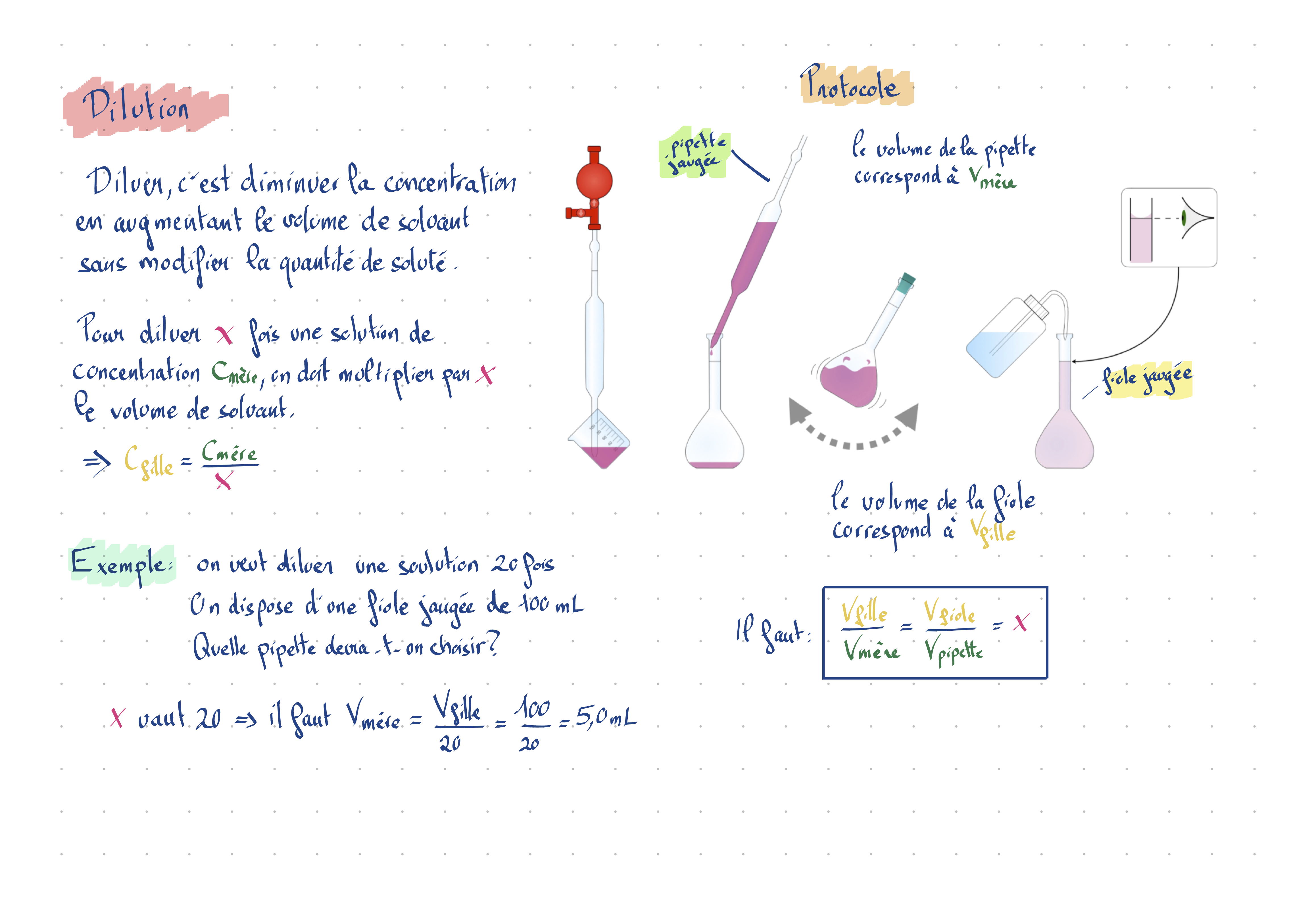
Donner le protocole d’une dilution et savoir déterminer les volumes de la pipette jaugée et de la fiole jaugée.
piege
Ne pas confondre la concentration massique et la masse volumique.
Les deux grandeurs ont la même dimension (masse sur volume), mais elles sont très différentes.
La concentration massique est le quotient de la masse de soluté (espèce minoritaire dissoute) par le volume du solvant. Il y a donc deux espèces en jeu, le soluté et le solvant.
La masse volumique est le quotient de la masse d’un corps par le volume de ce même corps. Cette grandeur est une propriété intrinsèque de ce corps.
De plus, la concentration massique est une grandeur chimique alors que la masse volumique est une grandeur physique, or on n’utilise pas les mêmes unités dans ces deux disciplines.
En chimie, l’unité de base du volume est le litre L et l’unité de base des masses est le gramme g, alors qu’en physique, on utilise les unités du système internationnal (USI) où les volumes sont en m3 et les masses en kg.
note
La densité est une version adimensionnée de la masse volumique.
On obtient la densité d’un objet en divisant sa masse volumique par la masse volumique de l’eau : $\displaystyle d = \frac{\rho}{\rho_{eau}}$ (avec $\rho_{eau}=\pu{1.00E3 kg * m-3}$ )
Rappels de cours
Simulations
- Comment faire pour augmenter la concentration (deux réponses) ?
- Comment faire pour diminuer la concentration ?
Exercice
Purification de l’eau (extrait sujet 2023 métropole)
Quiz
Combien un diamant de 24 carats contient-il de moles de carbone ?
> Donnée : 1 carat = 0,20 g
- [ ] sûrement beaucoup
- [ ] quelques unes
- [ ] environ 58 mol
- [x] environ 0,4 mol
## Dune du Pilat
La dune du Pilat compte-t-elle plus de grains de sable qu'un diamant d'1 mm3 compte d'atomes ?
> Données : volume de la dune : 55 millions de m3
densité du diamant : 3,51 - [ ] oui - [x] non > Et combien de temps passerait-on à compter les grains de sable de la dune ? - [ ] jaune ## Liquide physio
Pour créer du liquide physiologique, on dissout 0,90 g de sel (NaCl) dans 100 mL d’eau distillée.Quelle est la concentration massique en sel du liquide physio ?
- [ ] 11 L.g-1 - [ ] 90 g.L-1 - [x] 9,0 g.L-1 - [ ] 111 L.g-1 ## Liquide physio 2
Pour créer du liquide physiologique, on dissout 0,90 g de sel (NaCl) dans 100 mL d’eau distillée.Quelle est sa concentration molaire en ions chlorure $[\text{Cl}^{-}]$ ? > Données :
M(Na) = 23,0 g.mol-1
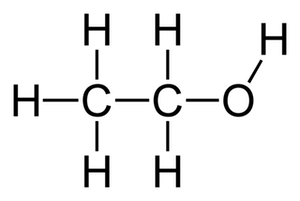
M(Cl) = 35,5 g.mol-1 - [ ] 25 mmol.L-1 - [ ] 1,5 mol.L-1 - [x] 0,15 mol.L-1 - [ ] 0,25 mol.L-1 ## Éthanol Combien de mol d’éthanol (dont la molécule est représentée ci-contre) sont contenues dans 5 mL ?
> Données :masse volumique de l'éthanol : $\rho=\pu{7,9E2 kg * m-3}$
$\text{M(O)} = \pu{16 g * mol-1}$ - [x] 87 mmol - [ ] 87 mol - [ ] Autre réponse