Puissance en régime sinusoïdal
Présentation
Rappels
En régime alternatif, que mesurent le voltmètre et l'ampèremètre en mode continu (DC ou ⎓) ?
La tension et l'intensité moyenne.
Et en mode alternatif (AC ou ∿), que mesurent-ils ?
La tension et l'intensité efficace.
Comment obtient-on $U_{eff}$ à partir de $U_{max}$ en régime sinusoïdal ?
$$U_{eff}=\frac{U_{max}}{\sqrt{2}}$$
Savoir et savoir faire
TP
Comment calculer numériquement la valeur de la puissance active d’un système à partir des évolutions temporelles de la tension et de l’intensité du courant ?
Lien vers l’exercice sur Colab (il faut vous connecter à un compte Google pour pouvoir exécuter le code).
Quiz
---
primary_color: steelblue
secondary_color: "#f2f2f2"
text_color: black
shuffle_questions: false
---
##
La relation qui permet de calculer la puissance active consommée par un dipôle est :
- [x] $P = kUI$
- [ ] $P = UI$
- [ ] $P = UI/k$
##
La relation qui permet de calculer la puissance apparente consommée par un dipôle est :
- [ ] $S = kUI$
- [x] $S = UI$
- [ ] $S = UI/k$
##
La relation qui permet de calculer le facteur de puissance est :
- [x] $k = P/S$
- [ ] $k = S/P$
- [ ] $k = PS$
##
Dans les relations donnant la puissance active $P$ et la puissance efficace $S$, les valeurs de la tension et de l'intensité sont :
- [x] les valeurs efficaces
- [ ] les valeurs moyennes
- [ ] les valeurs maximales
##
Une résistance soumise à une tension efficace de $\pu{45 V}$ et parcourue par une intensité efficace de $\pu{8,3 A}$ dissipe une puissance de :
- [x] $\pu{3,7E2 W}$
- [ ] $\pu{5,4 W}$
- [ ] $\pu{0,18 W}$
##
Un dipôle purement capacitif ou inductif :
- [ ] consomme de la puissance active
- [ ] ne fonctionne pas en régime sinusoïdal
- [x] ne consomme pas de puissance active
##
Pour un dipôle, on a :
tension aux bornes (en V) : $u(t)=110\sqrt{2}\cos(314t)$
intensité du courant (en A) : $i(t)=8\sqrt{2}\cos(314t-1,25)$
- [x] la tension efficace aux bornes de ce dipôle vaut 110 V
- [ ] la tension efficace aux bornes de ce dipôle vaut 156 V
- [ ] la tension efficace aux bornes de ce dipôle vaut 8 V
##
Pour un dipôle, on a :
tension aux bornes (en V) : $u(t)=110\sqrt{2}\cos(314t)$
intensité du courant (en A) : $i(t)=8\sqrt{2}\cos(314t-1,25)$
Pour ce dipôle, l'intensité efficace vaut :
- [x] 8 A
- [ ] 11 A
- [ ] 110 A
##
Que vaut la puissance efficace :
- [ ] $S = \pu{1760 VA}$
- [x] $S = \pu{880 VA}$
- [ ] $S = \pu{440 VA}$
##
On a représenté ci-dessous la puissance instantanée $p(t)$ :
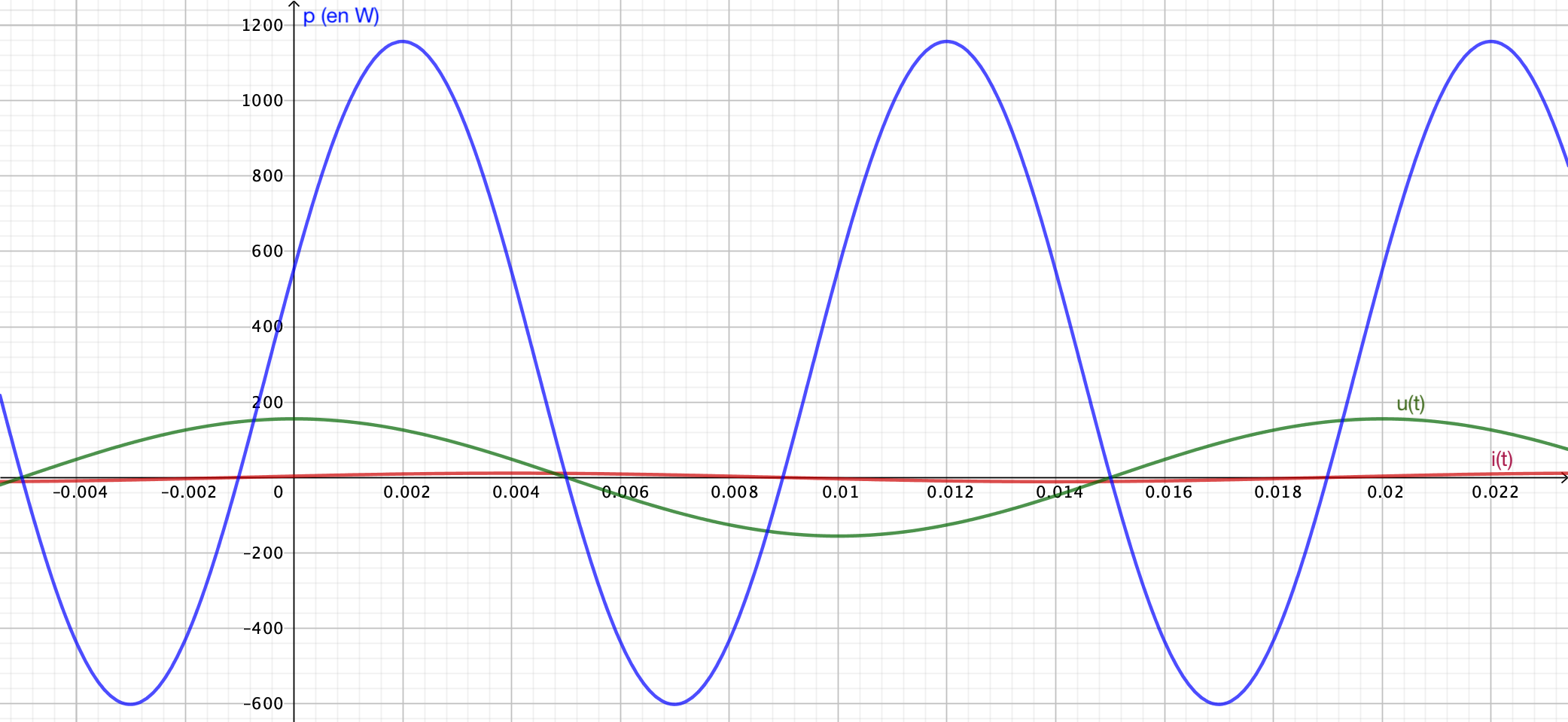
La puissance active consommée par le dipôle vaut :
- [x] $P = \pu{0,28 kW}$
- [ ] $P = \pu{1,16 kW}$
- [ ] $P = \pu{400 W}$
##
Le facteur de puissance vaut alors :
- [x] $k = 0,32$
- [ ] $k = 3,1$
- [ ] $k = 0,64$
##
Un dipôle qui absorbe une puissance active de $\pu{2,3 kW}$ et une puissance apparente de $\pu{3,5 kVA}$ a un facteur de puissance égal à :
- [ ] 1,5
- [x] 0,66
- [ ] 0,34
##
Pour mesurer une puissance active, on utilise :
- [ ] un voltmètre et un ampèremètre
- [x] un wattmètre
- [ ] un ohmmètre
##
Pour mesurer une puissance apparente, on utilise :
- [x] un voltmètre et un ampèremètre
- [ ] un wattmètre
- [ ] un ohmmètre