Diffraction et interférences
Documents
Quiz
---
primary_color: steelblue
secondary_color: "#f2f2f2"
text_color: black
shuffle_questions: false
---
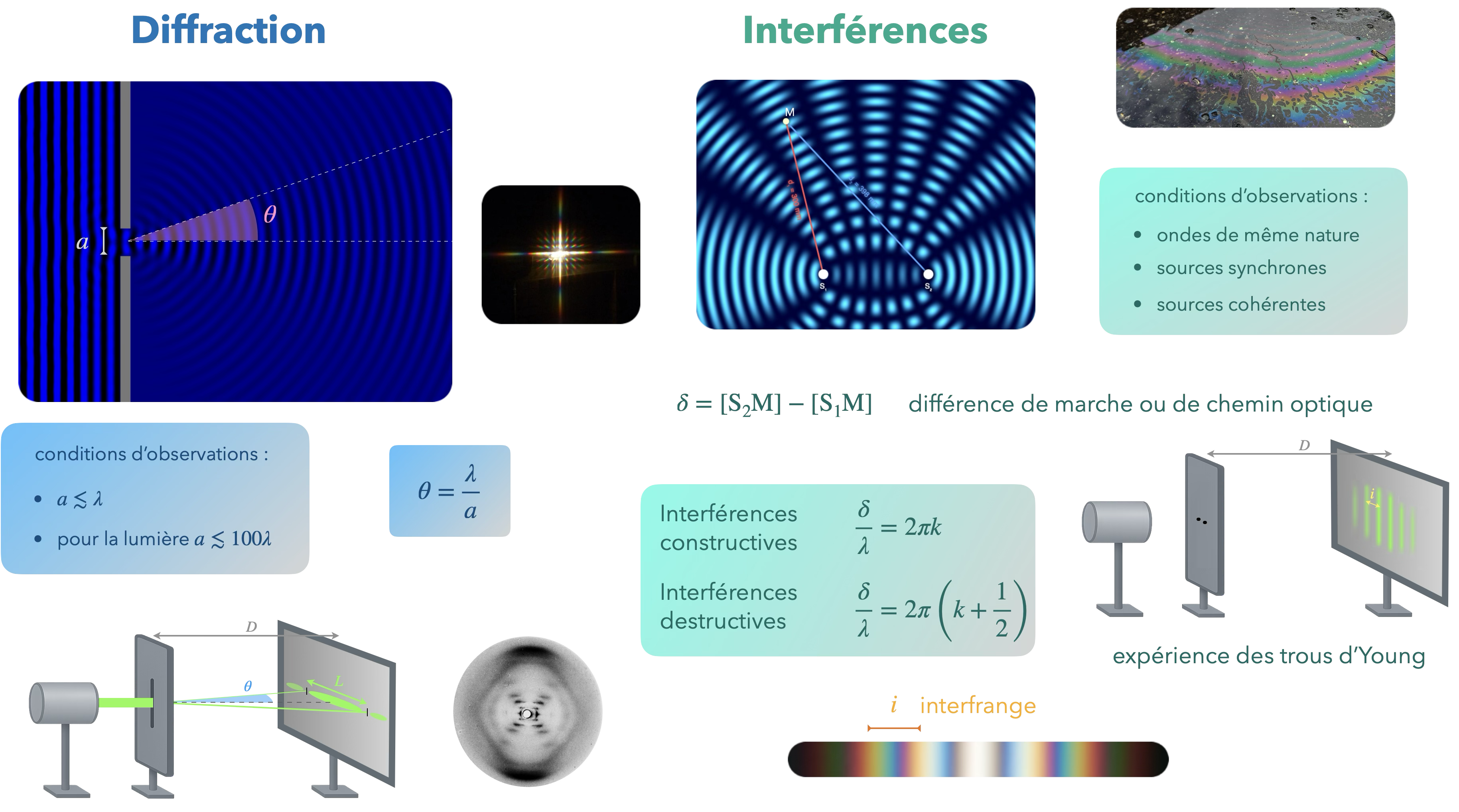
## Diffraction
La diffraction consiste en :
- [x] un étalement des directions d'une onde lorsqu'elle rencontre un obstacle ou une ouverture de petite dimension
- [ ] la superposition de deux ondes cohérentes
- [ ] le changement de direction du rayon lumineux lorsqu'il change de milieu
- [ ] l'absorption d'une onde par un milieu
## Largeur d'une fente
Une onde lumineuse de longueur d'onde $λ=\pu{500 nm}$ est diffractée par une fente de très grande longueur. Le premier minimum de diffraction est observé avec un angle $θ=\pu{0,1 rad}$ par rapport à l'axe central. Calculer la largeur de cette fente :
- [x] 5,0 µm
- [ ] 50 nm
- [ ] 5,0 mm
- [ ] 2,0 × 105 m
## Interférences constructives
Dans une zone où deux ondes interfèrent de manière constructive :
- [x] l'onde résultante a une amplitude plus élevée qu'une seule onde
- [ ] l'onde résultante a une amplitude plus faible qu'une seule onde
- [ ] l'onde résultante est déviée
- [ ] l'onde résultante est absorbée
## Interférences lumineuses
Pour obtenir des interférences lumineuses :
- [x] les ondes doivent provenir de sources cohérentes
- [ ] les ondes doivent avoir des amplitudes identiques
- [ ] les ondes doivent avoir des fréquences différentes
- [ ] les ondes doivent provenir de sources incohérentes
## Fentes d'Young (1)
Dans l'expérience des fentes d'Young, l'interfrange $i$ varie en fonction de la distance $D$ entre l'écran et les fentes d'Young de la façon suivante :
- [ ] l'interfrange $i$ diminue quand la distance $D$ augmente
- [x] l'interfrange $i$ augmente quand la distance $D$ augmente
- [ ] l'interfrange $i$ est indépendante de la distance $D$
- [ ] l'interfrange $i$ varie de façon non linéaire avec la distance $D$
## Fentes d'Young (2)
La relation entre l'interfrange $i$, la longueur d'onde $λ$, la distance $D$ entre les fentes et l'écran, et l'écart $b$ entre les fentes dans le dispositif d'Young est donnée par l'une des formules suivantes. En raisonnant sur les unités, indiquer celle qui est correcte.
- [x] $\displaystyle i=\frac{\lambda\!\cdot\! D}{b}$
- [ ] $\displaystyle i=\lambda\!\cdot\! D\!\cdot\! b$
- [ ] $\displaystyle i=\frac{\lambda\!\cdot\! D}{b^2}$
- [ ] $\displaystyle i=\frac{b}{\lambda\!\cdot\! D}$