Les modèles démographiques
Les croissances exponentielles
Question bonus : pourquoi la longueur des cordes d’un piano suit-elle une progression géométrique comme dans le dessin ci-dessous (réinvestissement du programme de 1ES) ? Quelle est la raison de la suite ?
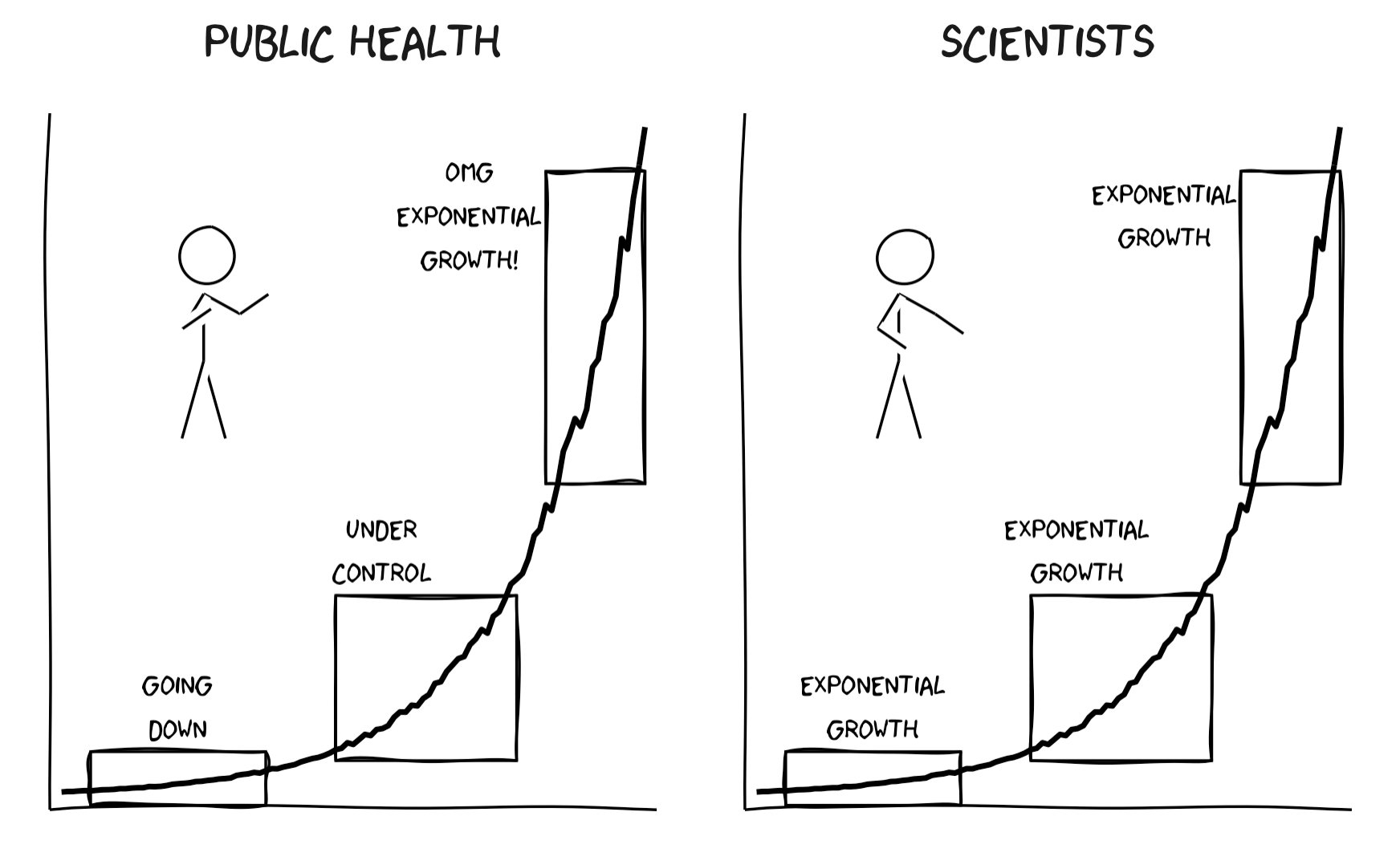
Croissance démographique
Selon Malthus (Essai sur le principe de population, 1798), en l’absence de limitation par la quantité de ressources disponibles, toute population croîtrait selon une progression géométrique. Et c’est bien ce que l’on observe un peu partout dans le monde au 19e et 20e siècle.
Malthus prévoyait par ailleurs que les moyens de subsistances ne pouvaient croître que de manière arithmétique rendant inéluctable le croisement entre ces deux croissances (population et ressources). L’économiste britannique prophétisait alors une paupérisation générale des populations si aucune politique de restriction des naissances n’était appliquée.
Ces idées ont eu un fort retentissement et sont parfois encore présentées comme du bon sens aujourd’hui bien que la réalité ait violemment battu en brèche le pronostic pessimiste de Malthus :
- 1960 : 3 milliards d’habitants, 2 milliards souffrant de malnutrition (soit 66 %)
- 2000 : 6 milliards d’habitants, 800 millions souffrant de malnutrition (soit 13,3 %)
Est-ce que cela nous assure pour autant que les ressources resteront suffisantes à l’avenir ? Réchauffement climatique, pollution, appauvrissement génétique des cultures, etc., peuvent malheureusement rebattre les cartes.
L’évolution des populations humaines au 21e siècle vient elle aussi contredire Malthus puisqu’on observe partout un décrochage par rapport aux croissances exponentielles du 20e siècle indépendant des moyens de subsistance.
Petit article en anglais qui décrit l’évolution de la population mondiale de 1700 à ajourd’hui puis jusqu’à la fin du siècle grâce aux prédictions de l’ONU.
Un article de CulturMaths pour les matheux curieux qui voudraient en savoir plus sur les modèles logistiques.

Activités
| Maths et croissance | Modèle de Malthus | Japon |
|---|---|---|
| appliquette geogebra | appliquette geogebra | appliquette geogebra 1 appliquette geogebra 2 appliquette geogebra 3 |