Course de tremplins
Deux balles dévalent chacune un tremplin différent dont les points de départ et d’arrivée ont même altitude :

Les différentes coordonnées sont données ci-dessous.
Les deux balles sont supposées ponctuelles et on prendra g = 9.8 m.s-2.
La boule jaune suit la ligne brisée ABC et la boule rouge suit ADEC.
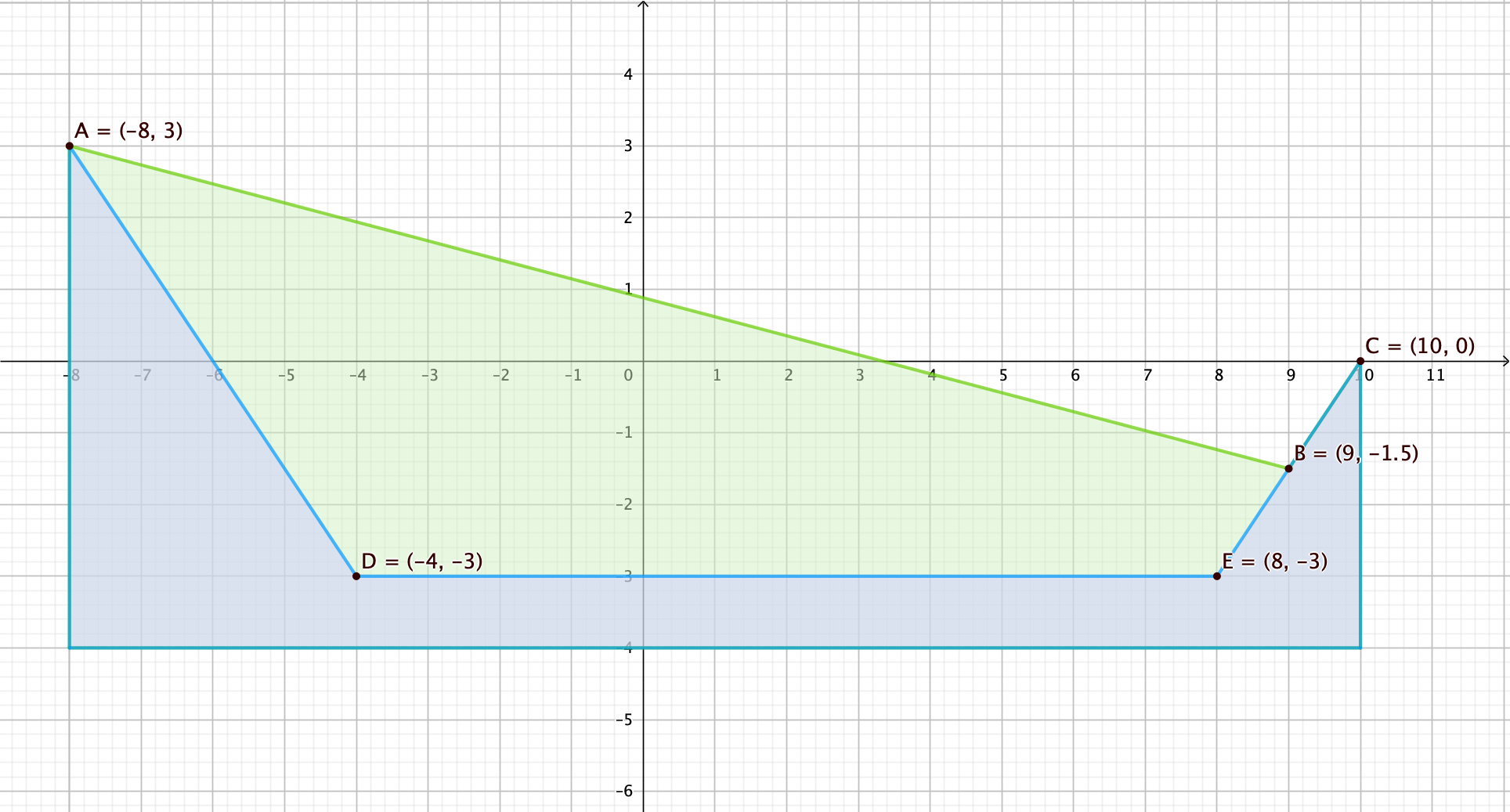
Questions préliminaires :
- Qulle balle atterrit le plus loin ?
- Quelle balle parcourt le moins de distance ?
- Quelle balle arrive la première en C ?
Vérification par simulation :
Résolution :
- Déterminer la durée mise pour chacune des balles pour atteindre le sol (y = -4). Confirmez-vous les valeurs de la simulation ? Commenter.
Vidéo de Bruce Yeany sur des tremplins ressemblants.
Petits suppléments : brachistochrone et tautochrone
Vous pouvez modifier sur le programme ci-dessous la courbe que suit la balle entre deux points fixes.
Vous pouvez tenter par exemple de construire le chemin le plus court ou envoyer directement la balle le plus bas possible, là où la vitesse est plus grande.
Que remarquez-vous sur les temps de parcours obtenus par rapport au temps de parcours sur la courbe initiale ?
Cette courbe est une cycloïde et s’appelle la brachistochrone.
Une autre cycloïde intéressante, la tautochrone.
Changez la position initiale de la balle verte sur la courbe, que remarquez-vous ?
Petite vidéo de Bruce Yeany donnant l’intuition pour comprendre la propriété de cette courbe.
Python :
Et pour finir, un lien vers un programme Python permettant de tracer la brachistochrone (utilisation de tableaux numpy, utilisation de la librairie scipy pour trouver une racine via la méthode de Newton et pour intégrer via quad, et utilisation de matplotlib pour tracer).