Correction
La respiration permet d’illustrer le premier principe de la thermodynamique sur un exemple qui nous est tous assez familier (j’espère).
On va supposer l’air comme étant un gaz parfait diatomique. Dans ces conditions, l’énergie interne de $n$ moles d’air vaut $U=\frac{5}{2}nRT$.
On ne considère dans la suite que les variations relatives du volume des poumons $\Rightarrow$ le volume $V$ avant inspiration (= après expiration) est pris comme égal à zéro.
De même, seules les pressions relatives nous intéressent $\Rightarrow$ la pression $P$ avant inspiration (= après expiration) est prise comme égale à zéro.
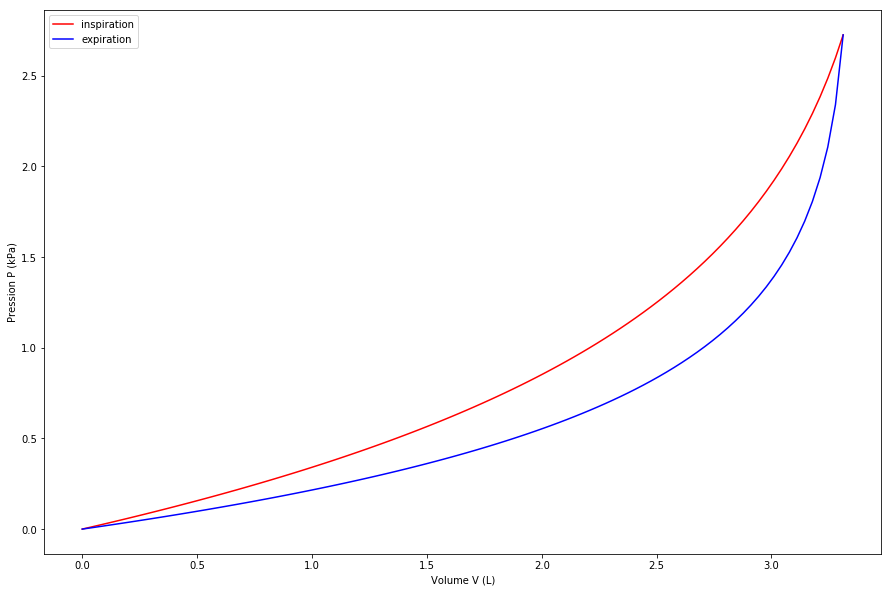
Une modélisation de $V(P)$ à partir de mesures expérimentales (faites pour $P$ grâce à un cathéter œsophagien et pour $V$ grâce à un pléthysmographe) donne :
- pour l’inspiration : $V=A_I\left(1-e^{-k_IP}\right)$
- pour l’expiration : $V=A_E\left(1-e^{-k_EP}\right)$
Avec $A_I=3,57\text{ L}$, $k_I=0,964.10^{-3}\text{ Pa}^{-1}$, $A_E=3,35\text{ L}$, $k_E=1,644.10^{-3}\text{ Pa}^{-1}$.
$A$ est la capacité pulmonaire maximale et $k$ est un coefficient de compressibilité.
$A_E<A_I$ car en fin d’expiration, des alvéoles se referment, s’affaissent, leurs parois se collant sous l’action de la tension superficielle (et ce malgré que le poumon produise des surfactants équivalents à ceux qu’on trouve dans le savon pour abaisser cette énergie de surface… Sans eux, c’est tout le poumon qui s’affaisserait). Et c’est aussi pourquoi $k_I>k_E$ ; à l’inspiration, il faut vaincre la tension de surface pour recruter à nouveau les alvéoles affaissées.
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import quad
from scipy.optimize import fsolve
A_I, A_E = 3.57, 3.35
k_I, k_E = 0.964, 1.644
def P_I(V): return 1/k_I*(np.log(A_I/(A_I-V)))
def P_E(V): return 1/k_E*(np.log(A_E/(A_E-V)))
def diff(V): return P_I(V)-P_E(V)
Vmax = min(A_E,A_I)
V_f = fsolve(diff,[1,Vmax-1e-5])[1]
P_f = P_I(V_f)
print(f"V_f = {V_f:.2f} L")
print(f"P_f = {P_f:.2f} kPa")
V = np.linspace(0,V_f,100)
plt.figure(figsize=(15,10),dpi=150)
plt.plot(V,P_I(V),c = "red", label="inspiration")
plt.plot(V,P_E(V),c = "blue",label="expiration")
plt.xlabel("Volume V (L)")
plt.ylabel("Pression P (kPa)")
plt.legend()
plt.show()
V_f = 3.31 L
P_f = 2.73 kPa
-
Déterminer numériquement les valeurs finales de volume et de pression $V_f$ et $P_f$ en fin d’inspiration / début d’expiration (on est sensé obtenir $V_f = 3,31\text{ L}$ et $P_f = 2,73\text{ kPa}$).
-
Reproduire la figure ci-dessus représentant $P(V)$ à l’inspiration et à l’expiration en utilisant la librairie
matplotlib. -
Lorsque la respiration n’est pas forcée, les muscles respiratoires ne travaillent que pendant l’inspiration (l’élasticité des poumons suffit pour l’expiration). Calculer ce travailnnumériquement. Et analytiquement, montrer qu’il vaut $-A_IP_f+P_fV_f+\frac{V_f}{k_I}$. Quelle proportion du métabolisme d’un humain moyen (10 MJ par jour) la respiration représente-t-elle ?
W = quad(P_I, 0, V_f)[0]
print(f"W = {W:.2f} J")
prop = 15*24*60*W/10e6*100 # pour 15 inspirations par minute
print(f"proportion du métabolisme : {prop:.2f} %")
W = 2.73 J
proportion du métabolisme : 0.59
$\begin{aligned} W&=-W_I &\text{le travail musculaire s’oppose au travail des forces de pression} \\ &=-\int_0^{V_f}-PdV \\ & =\int_0^{P_f}PA_I k_I e^{-k_I P}dP &\text{en utilisant }dV=A_Ik_Ie^{-k_IP}dP \\ & =A_Ik_I\left[\frac{-P}{k_I}e^{-k_I P}\right]_0^{P_f}-A_Ik_I\int_0^{P_f}\frac{-1}{k_I} e^{-k_I P}dP &\text{intégration par partie} \\ & =A_Ik_I\left[\frac{-P}{k_I}e^{-k_I P}\right]_0^{P_f}-A_Ik_I\left[\frac{1}{k_I^2}e^{-k_I P}\right]_0^{P_f} & \\ & =-A_I P_f e^{-k_I P_f}-\frac{A_I}{k_I}e^{-k_I P_f}+\frac{A_I}{k_I} \\ & =-A_IP_f+P_fV_f+\frac{V_f}{k_I}&\text{car }A_Ie^{-k_IP_f}=A_I-V_f \end{aligned}$
W = -A_I*P_f + P_f*V_f + V_f/k_I
print(f"W = {W:.2f} J")
W = 2.73 J
- Que vaut le transfert thermique $Q_I$ fourni à l’air lors d’une inspiration ?
$\Delta U_I = W_I + Q_I \Rightarrow Q_I = \Delta U_I - W_I$
$\begin{aligned}Q_I &= \frac{5}{2}(P_fV_f - 0)-\int_0^{V_f} -P dV\\&= \frac{5}{2}(P_fV_f - 0)-A_IP_f+P_fV_f+\frac{V_f}{k_I}\\&=\frac{7}{2}P_fV_f-A_I P_f +\frac{V_f}{k_I}\end{aligned}$
Q_I = 7/2*P_f*V_f - A_I*P_f+V_f/k_I
print(f"Q_I = {Q_I:.1f} J")
Q_I = 5/2*P_f*V_f + W
print(f"Q_I = {Q_I:.1f} J")
Q_I = 25.3 J
Q_I = 25.3 J
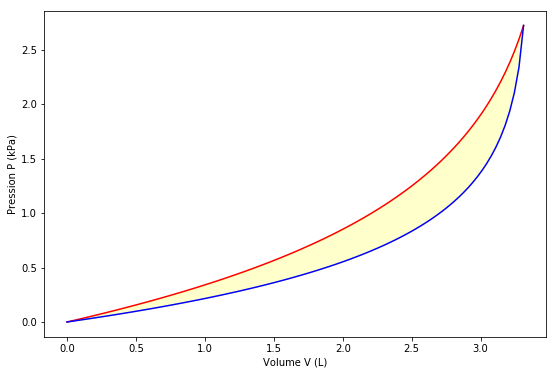
- Calculer le transfert thermique $Q$ lors d’un cycle respiratoire complet puis la puissance thermique libérée. Commenter son signe.
plt.figure(figsize=(9,6),dpi=150)
plt.plot(V,P_I(V),c = "red", label="inspiration")
plt.plot(V,P_E(V),c = "blue",label="expiration")
plt.xlabel("Volume V (L)")
plt.ylabel("Pression P (kPa)")
plt.legend()
plt.fill_between(V, P_I(V), P_E(V), color = "yellow", alpha = 0.2)
plt.show()
Q = quad(diff, 0, V_f)[0]
print(f"Q = {Q:.3f} J")
Plib = Q/4 # en prenant 4 s pour un cycle respiratoire (15 respirations par minute)
print(f"Plib = {Plib:.3f} W")
Q = 0.821 J
Plib = 0.205 W