Réfraction
Le champ de l’image fait 7 carreaux de largeur en dehors de l’eau mais seulement 5 sous l’eau. L’exercice vise dans un premier temps à expliquer cette observation puis à déterminer la distance entre le mur et la caméra.
- Observerait-on la même chose en immergeant sa tête sous l’eau, les yeux ouverts ? Et avec un masque ?
Correction
Les carreaux ne nous apparaitraient pas plus grands si on ouvrait les yeux sous l'eau. Par contre, ils nous apparaîtraient flous car les rayons de lumière sont moins réfractés lors de leur passage de l'eau au corps vitré (le milieu contenu dans l'œil d'indice optique 1,336). C'est comme si on était devenu très hypermétrope.Avec un masque ou des lunettes, on observerait la même chose que la caméra de la vidéo car c'est bien la couche d'air supplémentaire qui crée la réfraction responsable de l'agrandissement de l'image.
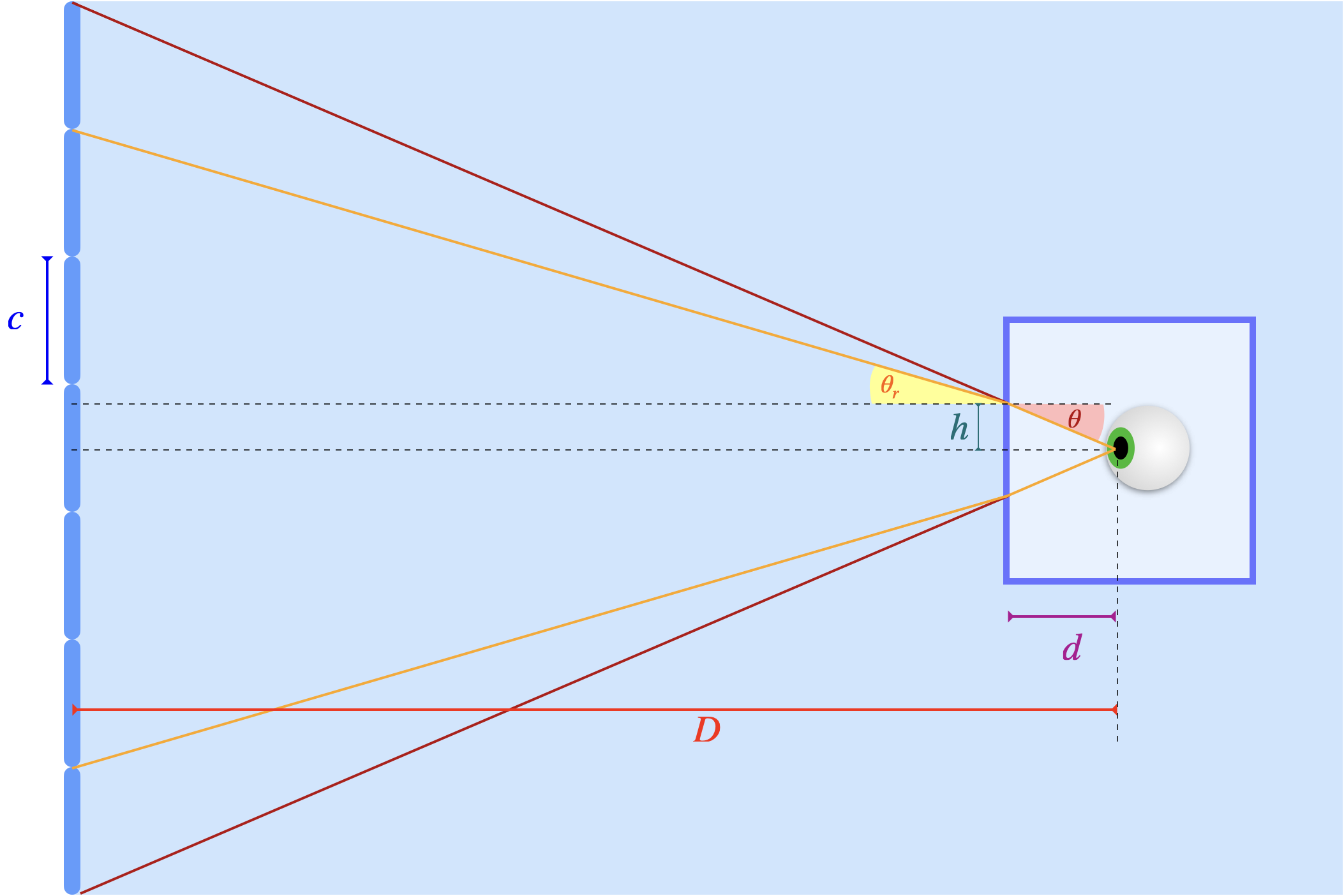
- Schématiser la situation lorsque la caméra est dans l’eau en représentant les rayons lumineux, les angles et en faisant apparaître les paramètres nécessaires.
Correction
On cherche maintenant à déterminer la distance $D$ entre la caméra et le mur.
- Écrire la relation liant $\theta$, $c$ et $D$.
Correction
$$\tan\theta = \frac{3,5\times c}{D}$$
- Écrire la relation liant $\theta_r$, $h$, $d$, $c$ et $D$.
Correction
$$\begin{aligned} (D-d)\tan\theta_r + h &= 2,5\times c\\ \tan\theta_r &= \frac{2,5\times c-h}{D-d} \end{aligned}$$
- Quelles approximations peut-on faire ?
Correction
$$d\ll D \;\text{ et }\;h\ll 2,5c$$ La relation précédente devient alors : $$ \tan\theta_r = \frac{2,5\times c}{D} $$
- Utiliser la relation de la question 3 et Snell-Descartes pour remplacer $\theta_r$ dans la relation de la question 4 (dans sa version simplifiée).
Correction
$$\begin{aligned} n_{air} \sin\theta &= n_{eau}\sin\theta_r\\ \Rightarrow \theta_r &= \sin^{-1}\left(\frac{n_{air}}{n_{eau}}\sin\theta\right) \end{aligned}$$ Et en utilisant la relation de la question 3 : $$\theta_r = \sin^{-1}\left(\frac{n_{air}}{n_{eau}}\sin\left(\tan^{-1}\left(\frac{3,5\times c}{D}\right)\right)\right)$$ $$\tan\theta_r = \frac{2,5c}{D}$$ devient donc : $$\tan \left(\sin^{-1}\left(\frac{n_{air}}{n_{eau}}\sin\left(\tan^{-1}\left(\frac{3,5\times c}{D}\right)\right)\right)\right)= \frac{2,5\times c}{D}$$
- Utiliser Python pour trouver graphiquement une approximation de la solution.
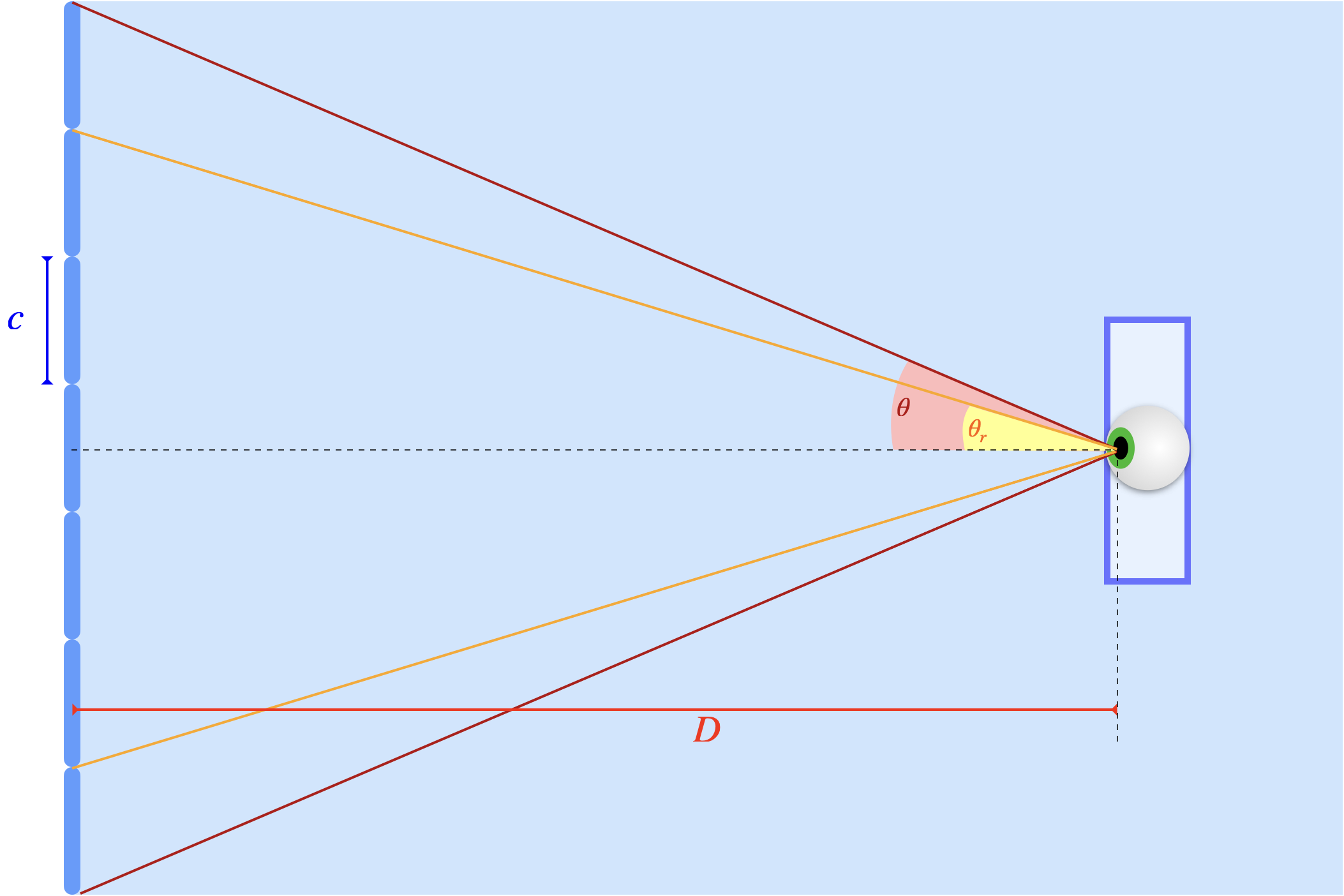
- Reschématiser la situation en prenant en compte les approximations faites à la question 4.
Correction
- En utilisant les deux triangles, déterminer algébriquement $D$ en fonction de $c$, $n_{eau}$ et $n_{air}$ (partir de Snell-Descartes et utiliser la trigonométrie et Pythagore).
Correction
$$ \begin{aligned} n_{air} \sin\theta &= n_{eau}\sin\theta_r\\ n_{air} \frac{3,5c}{\sqrt{D^2+(3,5c)^2}} &= n_{eau} \frac{2,5c}{\sqrt{D^2+(2,5c)^2}}\\ \Rightarrow n_{air}^2 \frac{(3,5c)^2}{D^2+(3,5c)^2} &= n_{eau}^2 \frac{(2,5c)^2}{D^2+(2,5c)^2} \end{aligned} $$ D'où
Pour $\pu{c = 5,0 cm}$, on trouve $\pu{D = 35 cm}$.$$D = 2,5 \times 3,5 \times c \times \sqrt{\frac{ n_{eau}^2-n_{air}^2}{(3,5 \times n_{air})^2 - (2,5 \times n_{eau})^2}}$$