Promenade
Alice part se promener en marchant à une vitesse de $\pu{2 km*h-1}$. Une heure après, Bob part avec un chien pour la rejoindre, en marchant à une vitesse de $\pu{4 km*h-1}$. Le chien étant agité, il fait des aller-retours entre les deux, à une vitesse de $\pu{10 km*h-1}$ jusqu’à ce qu’Alice et Bob se rejoignent. On veut déterminer la distance que le chien a parcouru ?
-
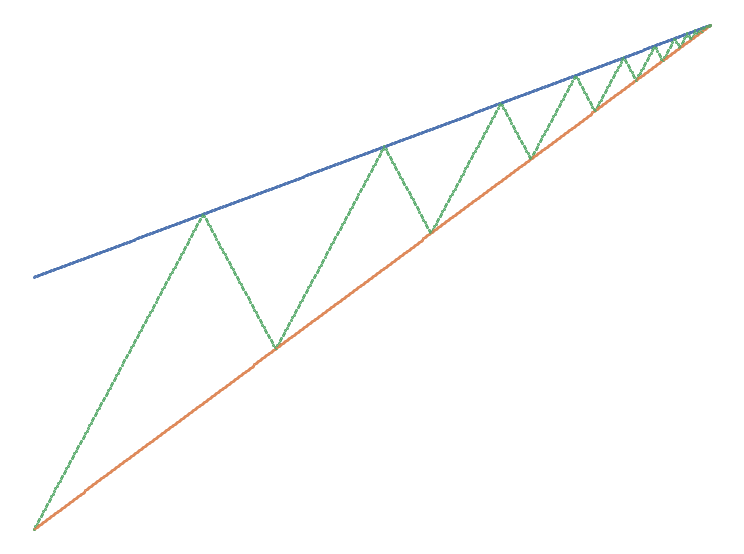
Superposer l’allure des courbes représentant l’abscisse sur le trajet de la promenade en fonction du temps pour Alice, Bob et le chien.
-
Appelons $D_n$ la distance séparant Alice et Bob au départ du $n$e aller-retour du chien (au moment où il repart vers Alice). Déterminer numériquement $\frac{D_{n+1}}{D_n}$ ainsi que la distance $d_n$ parcourue par le chien sur cet aller-retour.
-
En déduire la distance totale parcourue par le chien.
-
Comment aurait-on pu obtenir le résultat beaucoup plus rapidement ?