Redressement d’un œuf dur tournant
(extrait de l'épreuve CCP 2018 filière TPC)
Lorsqu’on impulse un mouvement rotatif très rapide (plus d’une dizaine de tours par seconde) à un œuf dur posé sur une surface bien plane et pas trop lisse, il se produit un étrange phénomène. Au bout de quelques tours, l’œuf se dresse et se met à tourner sur sa pointe ou sur sa base ! Lorsqu’il perd peu à peu de la vitesse par frottements, il finit par se remettre en position couchée, position où son centre de gravité est le plus bas.
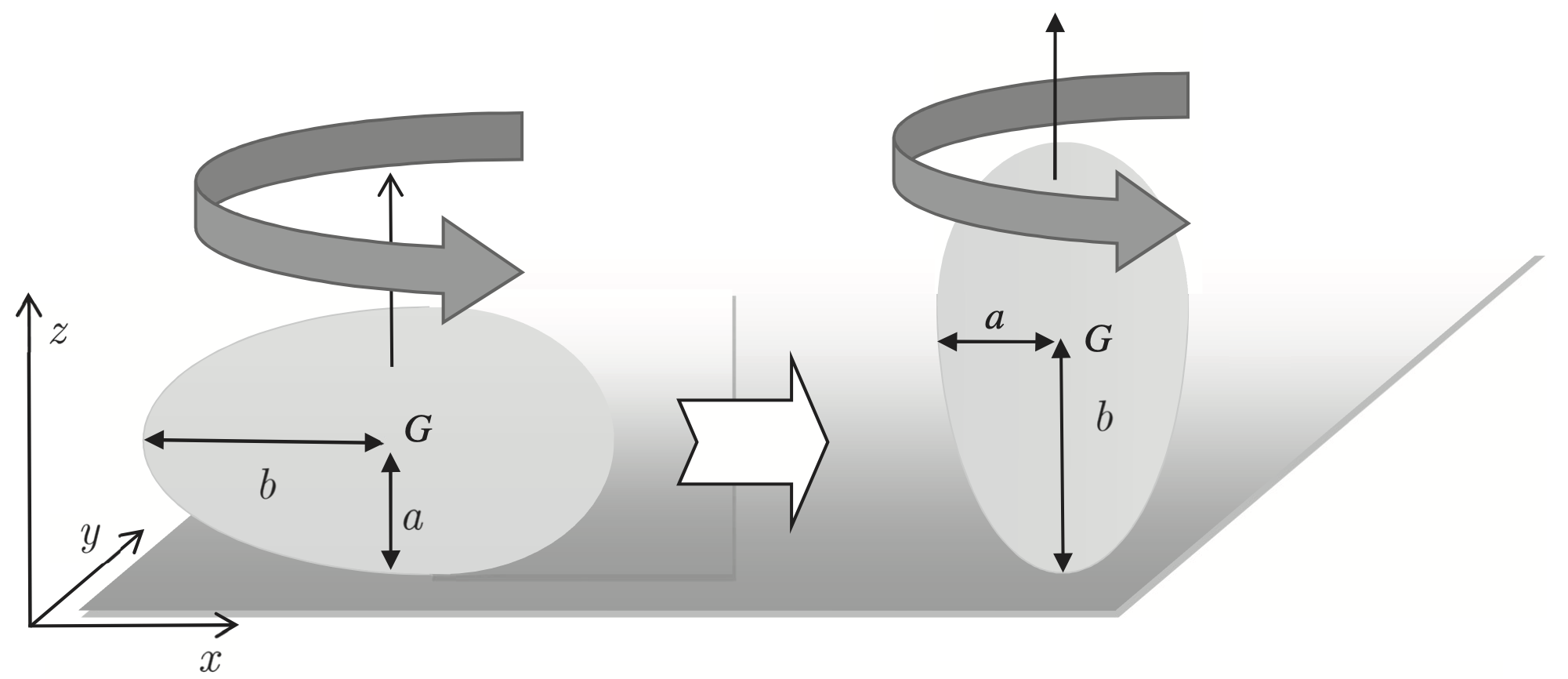
On ne considère que les états initial et final, on ne s’intéresse pas au mécanisme transitoire du redressement de l’œuf.
On modélise l’œuf dur par un ellipsoïde de révolution homogène de masse $m$, de demi petit axe $a$ et de demi grand axe $b$ (avec $a<b$). Le centre de masse $G$ est au centre de l’ellipsoïde (on néglige la légère asymétrie de l’œuf).
Les moments d’inertie d’un ellipsoïde de masse $m$ par rapport à son axe de rotation $Oz$ s’écrivent :
- $J_H=\frac{1}{5} m\left(a^2+b^2\right)$ lorsque l’œuf tourne à l’horizontale ;
- $J_V=\frac{2}{5} m a^2$ lorsque l’œuf tourne à la verticale.
On pose $\Omega$ la vitesse de rotation de l’œuf, qu’il soit dans sa position verticale ou horizontale.
-
Exprimer l’énergie mécanique totale de l’œuf dans les deux positions $E_{mH}$ et $E_{mV}$ en fonction des données. On choisira comme origine de l’énergie potentielle de pesanteur celle d’altitude nulle.
-
Montrer que pour $\Omega>\Omega_C$ pulsation limite, la position verticale est d’énergie inférieure à la position horizontale et assure le basculement d’une position à l’autre. On donnera l’expression de $\Omega_c$ en fonction de $g$, $a$ et $b$.
-
Calculer $\Omega_C$ pour $a=\pu{2,0 cm}$, $b=\pu{3,0 cm}$ et $g=\pu{10 m*s-2}$. Commenter le résultat obtenu en utilisant le petit texte introductif.
On suppose que le contact entre l’œuf et la table se fait sans frottement. Dans ce cas, lors du redressement de l’œuf, l’énergie doit être conservée. On fait tourner l’œuf en position horizontale, avec une vitesse angulaire initiale légèrement supérieure à la vitesse limite : $\Omega_0=\Omega_C+\varepsilon$ (avec $\varepsilon \ll \Omega_C$). L’œuf se redresse et tourne alors avec une vitesse angulaire finale $\Omega_f$ que l’on peut écrire sous la forme $\Omega_f=\Omega_C+r \varepsilon$ (avec $r$ un nombre sans dimension).
-
Exprimer les énergies mécaniques initiale $E_{mH}$ et finale $E_{mV}$ au premier ordre en $\varepsilon$.
-
En déduire, d’après les hypothèses, la valeur de $r$ en fonction de $a$ et de $b$. L’œuf a-t-il accéléré ou ralenti lors de son redressement ? Que vaudrait $r$ pour $a \simeq b$ ? Commenter.
-
Calculer les moments cinétiques $L_H$ et $L_V$ de l’œuf par rapport à l’axe $Oz$ avant et après son redressement. Exprimer la variation de moment cinétique $\Delta L = L_V-L_H$ en fonction de $\Omega_C$, $m$, $a$ et $b$. L’œuf a-t-il gagné ou perdu du moment cinétique lors de son redressement ?
-
Cette variation de moment cinétique signifie que, pendant le temps $\Delta t$ du redressement, l’œuf a subi un couple $\vec{C}$. Montrer que la composante verticale de ce couple par rapport à l’axe $Oz$ peut s’écrire :
$$C_z \simeq \frac{2 m g(a-b)}{\Omega_c \Delta t}$$
- Le poids ou la réaction normale du support peuvent-ils être responsables d’un tel couple ?
Y a-t-il une contradiction avec les hypothèses de l’énoncé ?