Le dôme de Norton
Le dôme de Norton est une expérience de pensée mise au point par John Norton en 2003. Elle a suscité un certain émoi dans la communauté scientifique en montrant qu’un comportement semblant non déterministe pouvait émerger des équations de Newton (elles, tout à fait déterministes).
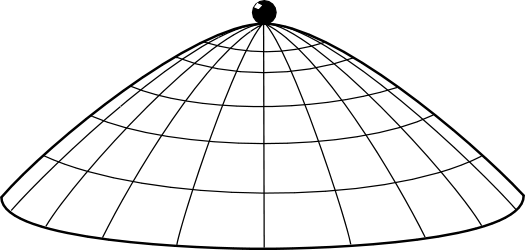
On modélise le dôme comme une surface de révolution autour de l’axe vertical passant par son sommet. Pour décrire la forme de ce dôme, on introduit une coordonnée curviligne $s$, définie comme la distance (le long de la surface) entre le sommet et le point considéré. À chaque valeur de $s$ est associée une différence d’altitude $h(s)$ entre le sommet et ce point, de sorte que : $$h(s)=\frac{2k}{3g}s^{3/2}\quad\text{où } k=1$$
Pour étudier le mouvement d’une bille sur cette surface, on se limite à une coupe transverse (plan vertical). Le point matériel (la bille) se repère alors par son abscisse curviligne $s(t)$, et l’on associe à ce mouvement un vecteur unitaire $\vec{u}_T$ tangent à la surface (et pointant vers l’aval de la pente) : $\overrightarrow{OM(t)}=s(t)\overrightarrow{u_T}$.
- Déterminer la dimension de la constante $k$.
- Montrer que la force tangentielle à la surface ressentie par la bille en un point du dôme est donnée par : $\overrightarrow{F_T}=mk\sqrt{s}\,\overrightarrow{u_T}$ (on négligera les frottements).
$$s(t) = \begin{cases} \frac{1}{144} (\sqrt{k}t-T)^4 & \text{si } t \geq T, \\ 0 & \text{si } t < T. \end{cases}$$
- Montrer que l’expression ci-dessus, où $T$ est un instant quelconque, est bien solution de l’équation donnée par la 2e loi de Newton.
- Pourquoi cela pose-t-il problème ?