Lentilles minces : démos
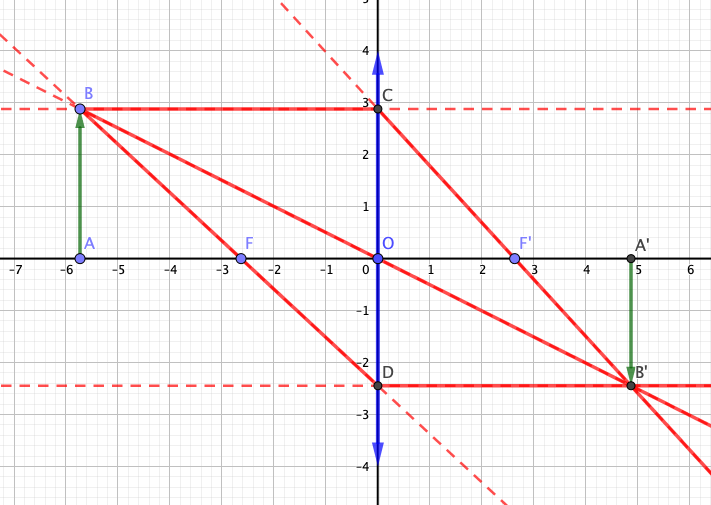
- En utilisant le schéma ci-dessus, démontrer la relation de conjugaison de Newton pour les lentilles minces qui stipule que : $$ \overline{A’F’}\cdot\overline{AF} = \overline{OF’}\cdot\overline{OF} $$
Correction
Thalès dans les traingles F'OC et F'A'B' : $$\frac{\overline{OF'}}{\overline{OC}}=\frac{\overline{A'F'}}{\overline{A'B'}}$$ Et comme $\overline{OC}=\overline{AB}$, on a : $$ \begin{equation} \frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{A'F'}}{\overline{OF'}} \end{equation} $$ Thalès dans FAB et FOD : $$\frac{\overline{OF}}{\overline{OD}}=\frac{\overline{AF}}{\overline{AB}}$$ Et comme $\overline{OD}=\overline{A'B'}$, on a : $$ \begin{equation} \frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{OF}}{\overline{AF}} \end{equation}$$ En combinant (1) et (2), on obtient : $$ \begin{equation} \overline{A'F'}\cdot\overline{AF} = \overline{OF'}\cdot\overline{OF} \end{equation} $$
- En introduisant le point $O$ pour décomposer les distances algébriques $\overline{AF}$ et $\overline{A’F’}$, partir de la relation de conjugaison de Newton pour obtenir celle de Descartes.
Correction
On écrit que $\overline{A'F'}=-\overline{OA'}+\overline{OF'}$ et que $\overline{AF}=-\overline{OA}+\overline{OF}$ et on utilise le fait que $\overline{OF}=-\overline{OF'}$.
En injectant tout ça dans (3), on obtient : $$ (-\overline{OA'}+\overline{OF'})(-\overline{OA}-\overline{OF'})=-(\overline{OF'})^2 $$ On développe : $$ \overline{OA'}\cdot\overline{OA}+\overline{OA'}\cdot\overline{OF'}-\overline{OF'}\cdot\overline{OA}\color{red}-{(\overline{OF'})^2}\color{black}=\color{red}{-(\overline{OF'})^2} $$ Les termes en rouge se simplifient et il ne nours reste plus qu'à diviser par le produit $\overline{OA}\cdot\overline{OA'}\cdot\overline{OF'}$ l'expression obtenue (aucune des trois distances ne doit donc être nulle) : $$ \frac{1}{\overline{OF'}}+\frac{1}{\overline{OA}}-\frac{1}{\overline{OA'}}=0 $$ Et en réarrangenat, on obtient bien la relation de conjugaison de Descartes :$$ \frac{1}{\overline{OA'}}-\frac{1}{\overline{OA}}=\frac{1}{\overline{OF'}} $$
- Quelle est la distance minimale entre un objet et son image ? Si la distance entre l’objet et l’écran est plus grande, combien de positions de la lentille permettent-elles d’avoir une image nette sur l’écran ? Les déterminer.