Lance-balle

Un lanceur de balle est fixé au sol mais le canon est libre de pivoter autour d’un axe horizontal.
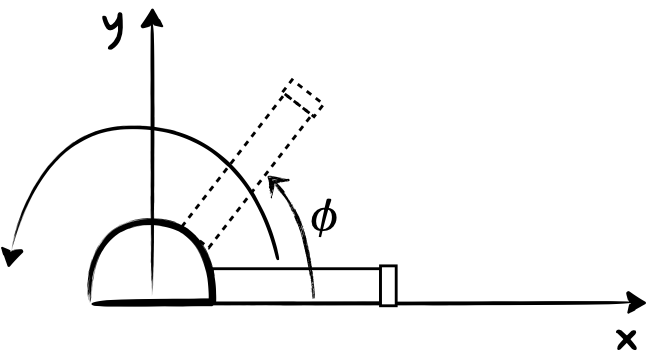
Le lanceur envoie ses projectiles avec toujours la même vitesse initiale $v_0$ mais avec un angle aléatoire distribué uniformément entre 0° et 180°.
-
Selon vous, chaque secteur découpant l’axe $x$ de manière régulière va-t-il recevoir autant de balles ? Si non, comment supposeriez-vous que la densité d’impacts $\frac{dN}{dx}$ sur un petit intervalle $dx$ évolue en fonction de $x$ ?
-
Déterminer les équations horaires du mouvement d’un projectile (pour une vitesse initiale $\overrightarrow{v_0}$ faisant un angle $\phi$ avec l’axe $x$ et en négligeant les frottements de l’air).
-
En déduire l’équation de la trajectoire de la balle.
-
Déterminer la portée $x(\phi)$ de la balle en fonction de l’angle $\phi$.
-
En appelant $N_{tot}$ le nombre de balles envoyées en tout, déterminer le nombre $N(\phi)$ de balles envoyées avec un angle compris entre 0 et $\phi$. En déduire $\frac{dN}{d\phi}$.
-
En utilisant le fait qu’on puisse écrire (dans les conditions de l’exercice) que $\frac{dN}{d\phi} = \frac{dN}{dx} \frac{dx}{d\phi}$, déterminer la densité $\frac{dN}{dx}$ d’impacts de balles entre $x$ et $x+dx$.
-
Vérifier en complétant le code python de ce notebook.
Correction
Exemple de solution :from random import random from math import cos,sin,pi N = 50000 v0 = 20 g = 10 dt = 1e-3 x_sol = [] for i in range(N): phi = random()*pi x = 0 y = 0 vx = v0*cos(phi) vy = v0*sin(phi) while y >= 0: vy += -g*dt x += vx*dt y += vy*dt x_sol.append(x)