Clothoïde
Pour opérer un virage, on choisit d’abord de connecter deux sections de rails rectilignes (en orange) de directions différentes par un arc de cercle (bleu).
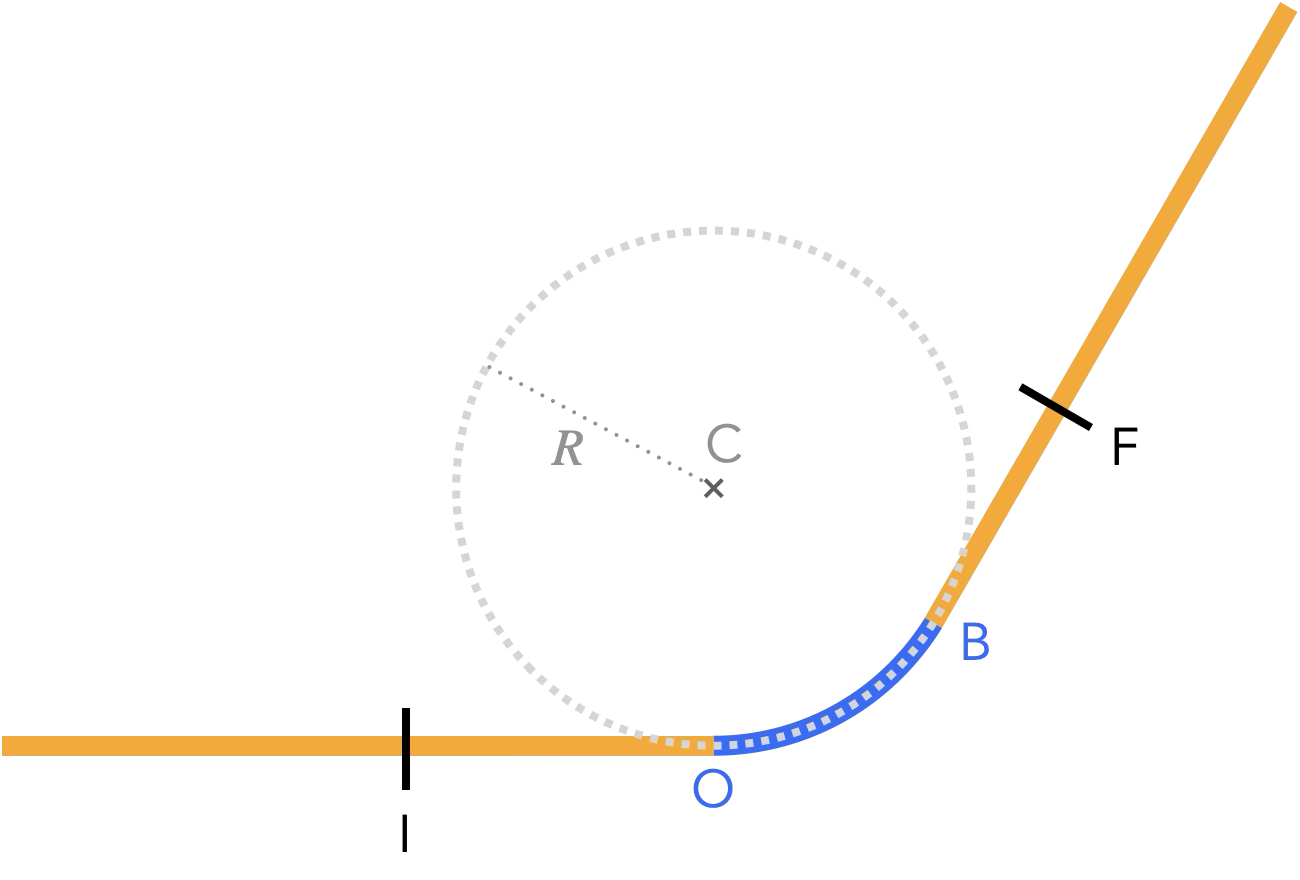
-
Tracer l’évolution de l’accélération d’un point $\mathrm{M}$ suivant les rails à vitesse constante sur le trajet entre $\mathrm{I}$ et $\mathrm{F}$.
-
Ce raccordement est-il une bonne idée ?
Plutôt qu’un arc de cercle, on va relier les deux portions rectilignes par des morceaux de clothoïdes1. Cette courbe a pour particularité que son rayon de courbure croit linéairement avec l’abscisse curviligne sur la courbe.
Supposons qu’un point $\mathrm{M}$ suive une clothoïde à vitesse constante $v=\pu{1,0 m*s-1}$. On peut alors paramétrer la courbe avec le temps $t$. Plaçons l’origine en $\mathrm{M}(t=0)$. Le rayon de courbure $R(t)$ en $\mathrm{M}(t)$ vaut alors $\frac{1}{R(t)}=kt$ où $k$ est une constante positive.
-
Esquisser l’allure d’une clothoïde.
-
Dans un repère de Frenet, écrire l’accélération tangentielle et normale du point M.
-
Reprendre les questions 1 et 2 avec un tronçon de raccordement fait à partir de deux tronçons de clothoïdes symétriques par rapport à l’axe ($\Delta$). L’origine de la première clothoïde est en O et celle de la deuxième en B.
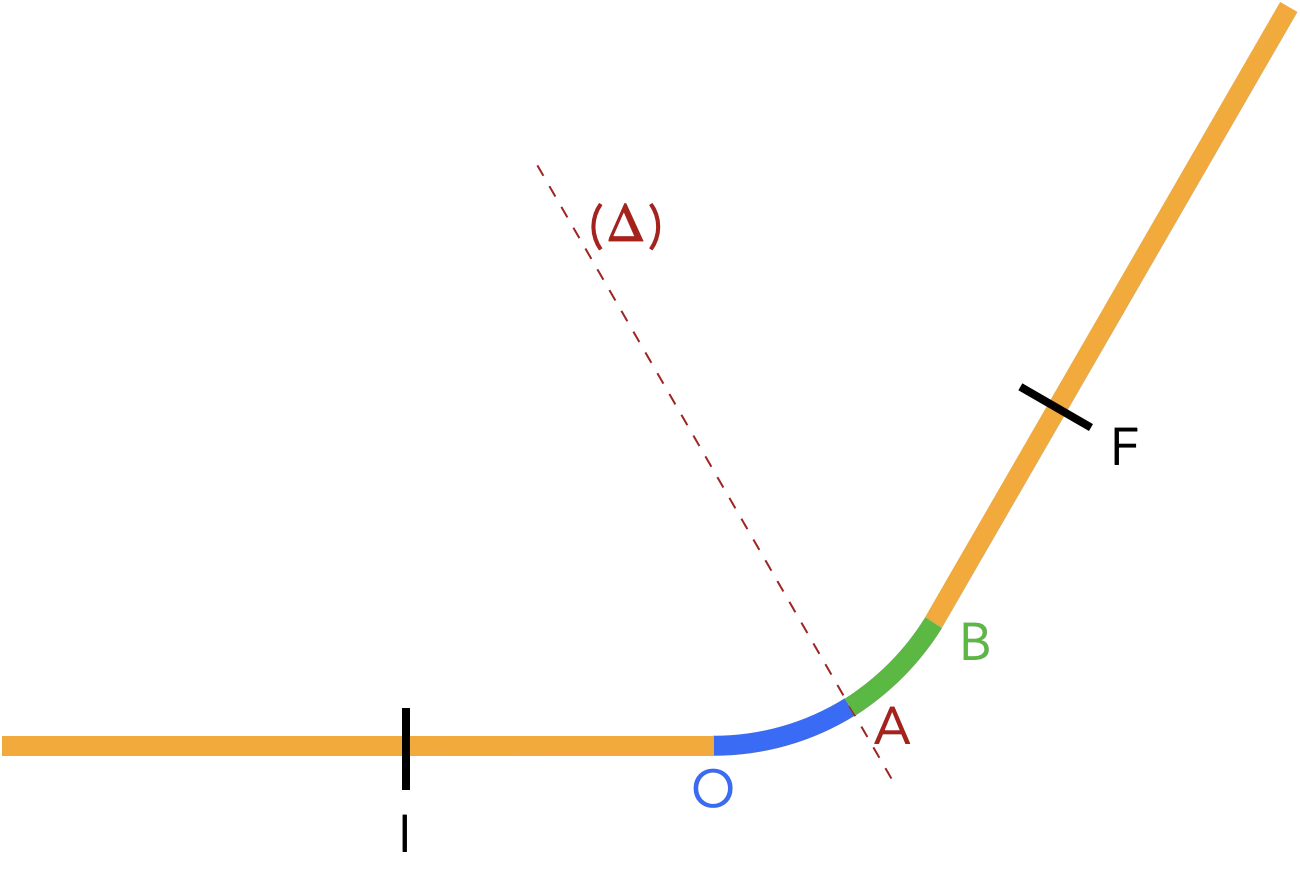
On veut maintenant tracer un tronçon de clothoïde et pour cela, il faut trouver son équation.
-
En appelant $\theta$ l’angle que fait le vecteur tangent $\vec{u}_T(t)$ au point $\mathrm{M}(t)$ de la courbe avec l’axe $\mathrm{O}x$, montrer que : $$\theta(t)=\frac 12 k v t^2$$
-
En déduire que l’équation de la clothoïde est donnée par : $$ \begin{cases} v\int_0^t \cos\left(\frac 12 kv u^2\right)\mathrm{d}u\\ v\int_0^t \sin\left(\frac 12 kv u^2\right)\mathrm{d}u \end{cases} $$
-
En utilisant la méthode des rectangles, représenter graphiquement un tronçon de clothoïde pout $t$ allant de 0 à 5 s sur Python en complétant le code suivant.
import numpy as np
import matplotlib.pyplot as plt
def integrale(f,a,b):
#################
## À COMPLÉTER ##
#################
v = 1
k = 2
t = np.linspace(0,5,500)
def c(x):
return v * np.cos(1/2 * k * v * x**2)
def s(x):
return v * np.sin(1/2 * k * v * x**2)
def C(x):
return integrale(c,0,x)
def S(x):
return integrale(s,0,x)
plt.figure(figsize=(6, 6),dpi=150)
plt.plot(C(t),S(t))
plt.show()
-
Clotho est la benjamine des trois Moires, celle qui tisse le fil de la vie (ça a donné l’anglais clothe) ; les deux autres tirent (Lachésis) et découpent (Atropos) dans la mythologie grecque antique. On appelle aussi la clothoïde spirale de Cornu ou d’Euler ou de Fresnel… ↩︎