TP variation de vitesse
Vous allez devoir faire un pointage vidéo d’une chute libre à l’aide de l’application fizziq puis analyser le mouvement grâce à des petits codes python qui vont nous permettre de tracer les vecteurs déplacement, vitesse et variation de vitesse.
Les données que j’utilise dans les exemples sont issues du pointage de la vidéo “parabolique” de l’application.
Vous devrez obtenir vos propres données !
La situation à filmer est une chute libre comme sur le schéma suivant. Le smartphone devra être tenu bien verticalement et ne devra pas bouger pendant tout l’enregistrement. Une règle devra être disposée dans le plan du mouvement pour servir d’échelle. La vitesse d’enregistrement devra être normale et l’ensemble de la parabole devra être capturée.

Pour pointer la vidéo et obtenir les données, suivre le petit tuto ci-dessous (des choses ont changé dans l’application mais vous devriez pouvoir vous y retrouver).
Une fois les résultats obtenus, il faudra recopier les valeurs de t, x et y dans la première cellule du notebook accompagnant ce TP.
⚠️ Il faut utiliser le point et non la virgule comme séparateur décimal et les différentes valeurs sont séparées par des virgules.
L’exécution de chaque cellule se fait en cliquant sur le rond avec un symbole lecture en haut à gauche de la cellule (voir image ci-dessous).
À l’exécution de la première cellule, Colab vous demandera de vous connecter à un compte Google.
Dans mon cas, les mesures donnent :
T = [0.000,0.033,0.066,0.099,0.132,0.165,0.198,0.231,0.264,0.297,0.330,0.363,0.396,0.429,0.462,0.495,0.528,0.561,0.594,0.627,0.660,0.693,0.726,0.759,0.792,0.825,0.858,0.891]
X = [-0.037,-0.007,0.022,0.052,0.081,0.110,0.139,0.170,0.201,0.230,0.259,0.289,0.319,0.348,0.378,0.408,0.437,0.467,0.497,0.526,0.556,0.587,0.618,0.648,0.677,0.707,0.736,0.767]
Y = [0.383,0.527,0.659,0.781,0.893,0.994,1.082,1.164,1.233,1.291,1.338,1.376,1.402,1.418,1.422,1.416,1.399,1.372,1.334,1.285,1.226,1.156,1.074,0.984,0.882,0.769,0.645,0.511]
Une fois vos propres mesures copiées, pensez à exécuter la cellule les contenant. Les cellules de code devront être exécutées les unes après les autres (ce ne sont pas des programmes indépendants ; une fois qu’une liste est en mémoire, elles l’est pour toutes les cellules exécutées ultérieurement).
Si on a beaucoup de points, il peut être judicieux de n’en prendre qu’un sur deux pour rendre les résultats plus lisibles. C’est la mission de la cellule suivante.
if len(T) > 20:
a = 2
else:
a = 1
t = T[::a] # nouveaux
x = X[::a] # noms
y = Y[::a] # des listes
N = len(t) # Nombre d'éléments
Dt = t[1]-t[0] # Δt
print(N,Dt)
14 0.066
L’affichage obtenu montre que dans mon cas, la liste des temps contient maintenant 14 éléments (au lieu de 28) et que l’écart temporel $\Delta t$ entre deux images est de 0,066 s au lieu de 0,033 s (le framerate de la vidéo est de 30 images par seconde).
Vecteurs déplacement
Dans la cellule suivante, on va tracer les positions de la balle ainsi que les vecteurs déplacement entre chaque point.
Le vecteur déplacement $\overrightarrow{MM’}$ entre $M$ et $M’$ est ici décomposé en un vecteur déplacement horizontal $\overrightarrow{{MM’}_x}$ et un vecteur déplacement vertical $\overrightarrow{{MM’}_y}$ (avec $\overrightarrow{MM’} = \overrightarrow{{MM’}_x} + \overrightarrow{{MM’}_y}$).
On ne veut pas qu’un seul vecteur déplacement mais plutôt les vecteurs déplacements entre chaque paire de points consécutifs.
Pour ça, on crée d’abord deux listes de $N-1$ éléments remplis de zéros ($N-1$ car on a $N$ points et donc $N-1$ déplacements entre ces points) appelées MMprime_x et MMprime_y.
Puis, à l’aide d’une boucle où la variable i parcourt les entiers de $0$ à $N-1$, on remplace chaque élément MMprime_x[i] (valant jusqu’ici $0$) de la liste MMprime_x par X[i+1]-X[i] et chaque élément MMprime_y[i] par Y[i+1]-Y[i].
import matplotlib.pyplot as plt
plt.style.use("seaborn-v0_8")
### Calcul de tous les vecteurs déplacement entre deux points consécutifs :
MMprime_x = [0 for i in range(N-1)]
MMprime_y = [0 for i in range(N-1)]
for i in range(N-1): # on s'arrête à l'avant-dernier point
MMprime_x[i] = x[i+1] - x[i]
MMprime_y[i] = y[i+1] - y[i]
### Tracés :
plt.figure(figsize=(12, 6),dpi=150)
plt.scatter(x, y, zorder=2)
for i in range(N-1):
plt.annotate('', xy=(x[i] + MMprime_x[i], y[i] + MMprime_y[i]), xytext=(x[i], y[i]), arrowprops=dict(facecolor='#00AB8E',edgecolor='none'), zorder=1)
plt.title('Représentation des positions de la balle et des vecteurs déplacement')
plt.xlabel('x (m)')
plt.ylabel('y (m)')
#plt.axis('equal')
plt.xlim(min(x)-0.1, max(x)+0.1)
plt.ylim(min(y)-0.1, max(y)+0.1)
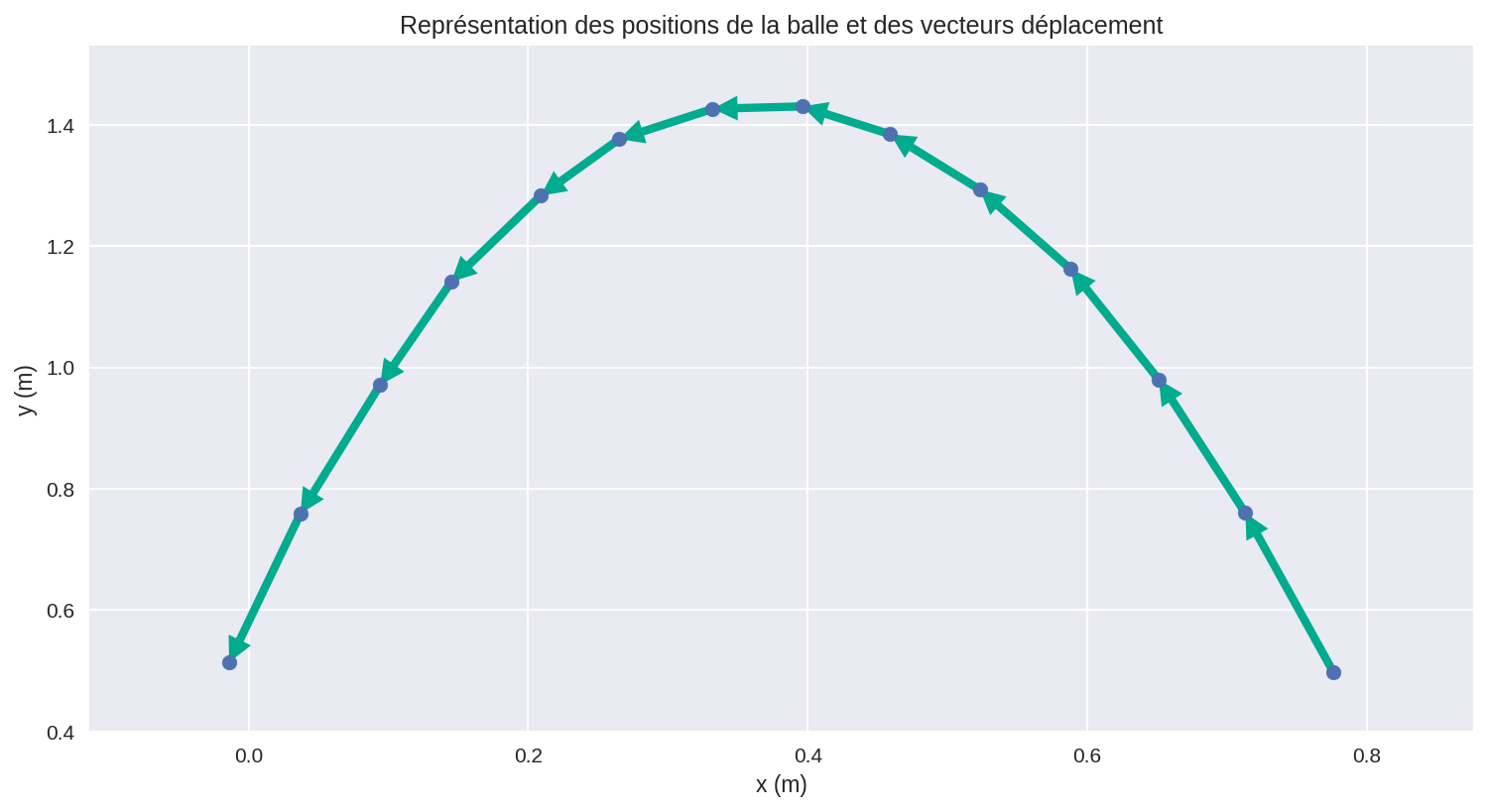
- Décrire le mouvement de l’objet.
Vecteurs vitesse
Traçons ensuite les vecteurs vitesse à partir des vecteurs déplacement.
- Complétez le code permettant de calculer
V_x[i]etV_y[i]à partir deMMprime_x[i]etMMprime_y[i]et deDt(qui est défini deux cellules plus haut).
Aide : il suffit d’appliquer la définition de la vitesse pour un déplacement $\overrightarrow{MM’}$ pendant une durée $\Delta t$, mais comme on a décomposé le vecteur déplacement en une composante horizontale et une composante verticale, on se retrouve avec une vitesse horizontale $\vec{v_x}$ et une vitesse verticale $\vec{v_y}$.
# Calcul des vecteurs vitesse :
V_x = [0 for i in range(N-1)]
V_y = [0 for i in range(N-1)]
############ PARTIE À COMPLÉTER ############
for i in range(N-1):
V_x[i] =
V_y[i] =
############################################
# Positions des extrémités des vecteurs :
echelle = 1/10 # permet d'ajuster la taille des vecteurs
finVx = [0 for i in range(N-1)]
finVy = [0 for i in range(N-1)]
for i in range(N-1):
finVx[i] = x[i] + V_x[i]*echelle
finVy[i] = y[i] + V_y[i]*echelle
# Tracés :
plt.figure(figsize=(12, 8),dpi=150)
plt.scatter(x, y, zorder=2)
for i in range(N-1):
plt.annotate('', xy=(finVx[i], finVy[i]), xytext=(x[i], y[i]), arrowprops=dict(facecolor='#FFD932',edgecolor='#FEAE00'), zorder=1)
plt.text(x[i] + V_x[i]*echelle-1/15, y[i] + V_y[i]*echelle/1, f'{(V_x[i]**2+V_y[i]**2)**0.5:.1f} m/s', fontsize=9, color='#FEAE00')
plt.title('Représentation des positions de la balle et des vecteurs vitesses')
plt.xlabel('x (m)')
plt.ylabel('y (m)')
#plt.axis('equal')
plt.xlim(min(x+finVx)-0.1, max(x+finVx)+0.1)
plt.ylim(min(y+finVy)-0.1, max(y+finVy)+0.1)
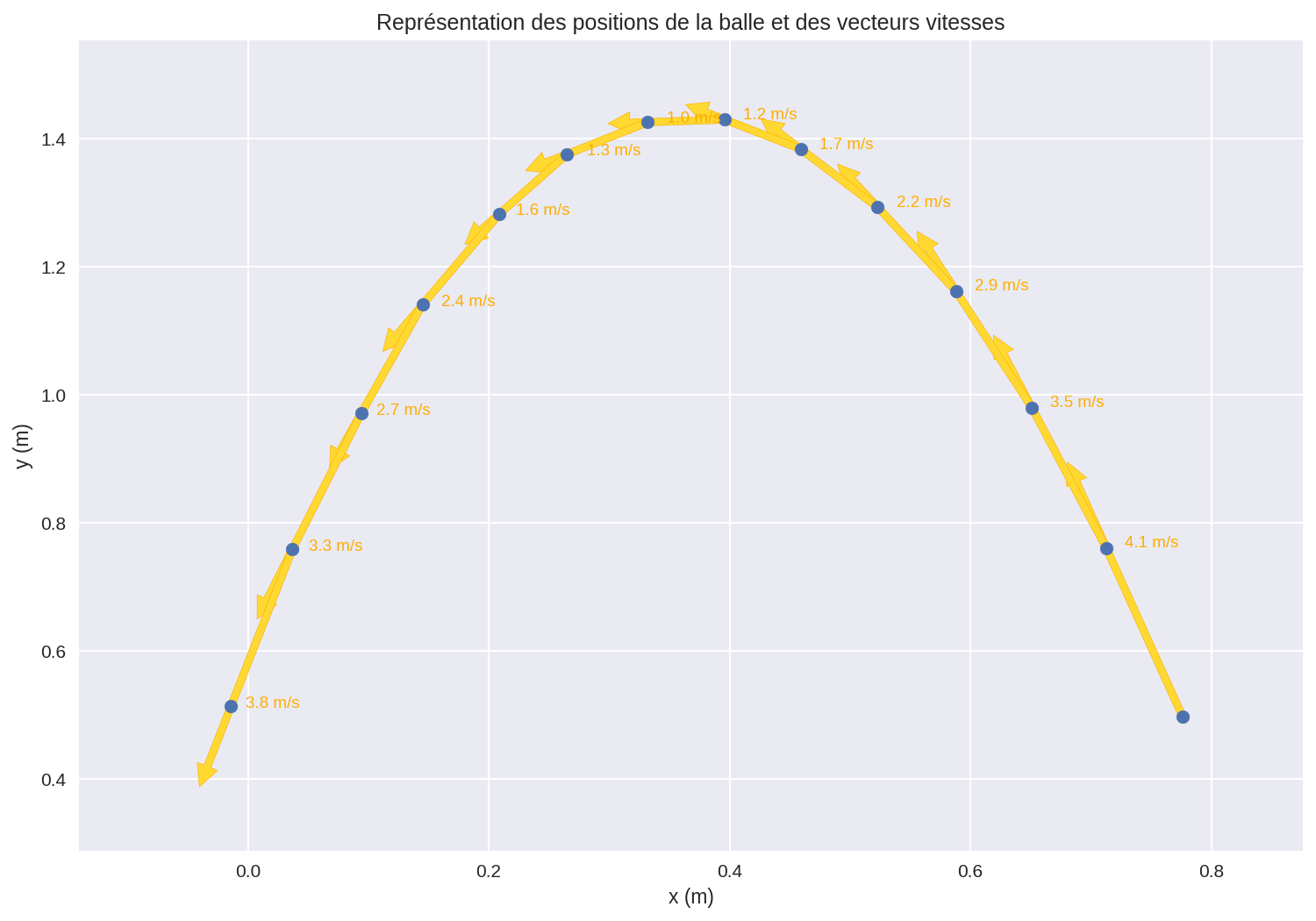
Vecteurs variation de vitesse
On va maintenant étudier et tracer le vecteur “variation de vitesse” (différence entre le vecteur vitesse du point suivant et celui du point considéré). L’idée est d’étudier comment varie le vecteur vitesse puisque cette variation témoigne directement de l’action subie :
une force modifie le vecteur vitesse dans sa direction et son sens.
- Compléter le code permettant de calculer
DV_x[i]etDV_y[i].
Aide : inspirez-vous du code ayant permis d’obtenir les vecteurs déplacements horizontaux et verticaux à partir des listes X et Y.
# Calcul des vecteurs "variation de la vitesse" :
DV_x = [0 for i in range(N-2)]
DV_y = [0 for i in range(N-2)]
############ PARTIE À COMPLÉTER ############
for i in range(N-2):
DV_x[i] =
DV_y[i] =
############################################
# Positions des extrémités des vecteurs :
echelle = 1/3
finDVx = [0 for i in range(N-2)]
finDVy = [0 for i in range(N-2)]
for i in range(N-2):
finDVx[i] = x[i] + DV_x[i]*echelle
finDVy[i] = y[i] + DV_y[i]*echelle
# Tracés :
plt.figure(figsize=(12, 6),dpi=150)
plt.scatter(x, y, zorder=2)
for i in range(N-2):
plt.annotate('', xy=(finDVx[i], finDVy[i]), xytext=(x[i], y[i]), arrowprops=dict(facecolor='#1DB100',edgecolor='none'), zorder=1)
plt.title('Représentation des positions de la balle et des vecteurs variation de vitesse')
plt.xlabel('x (m)')
plt.ylabel('y (m)')
plt.xlim(min(x+finDVx)-0.1, max(x+finDVx)+0.1)
plt.ylim(min(y+finDVy)-0.1, max(y+finDVy)+0.1)
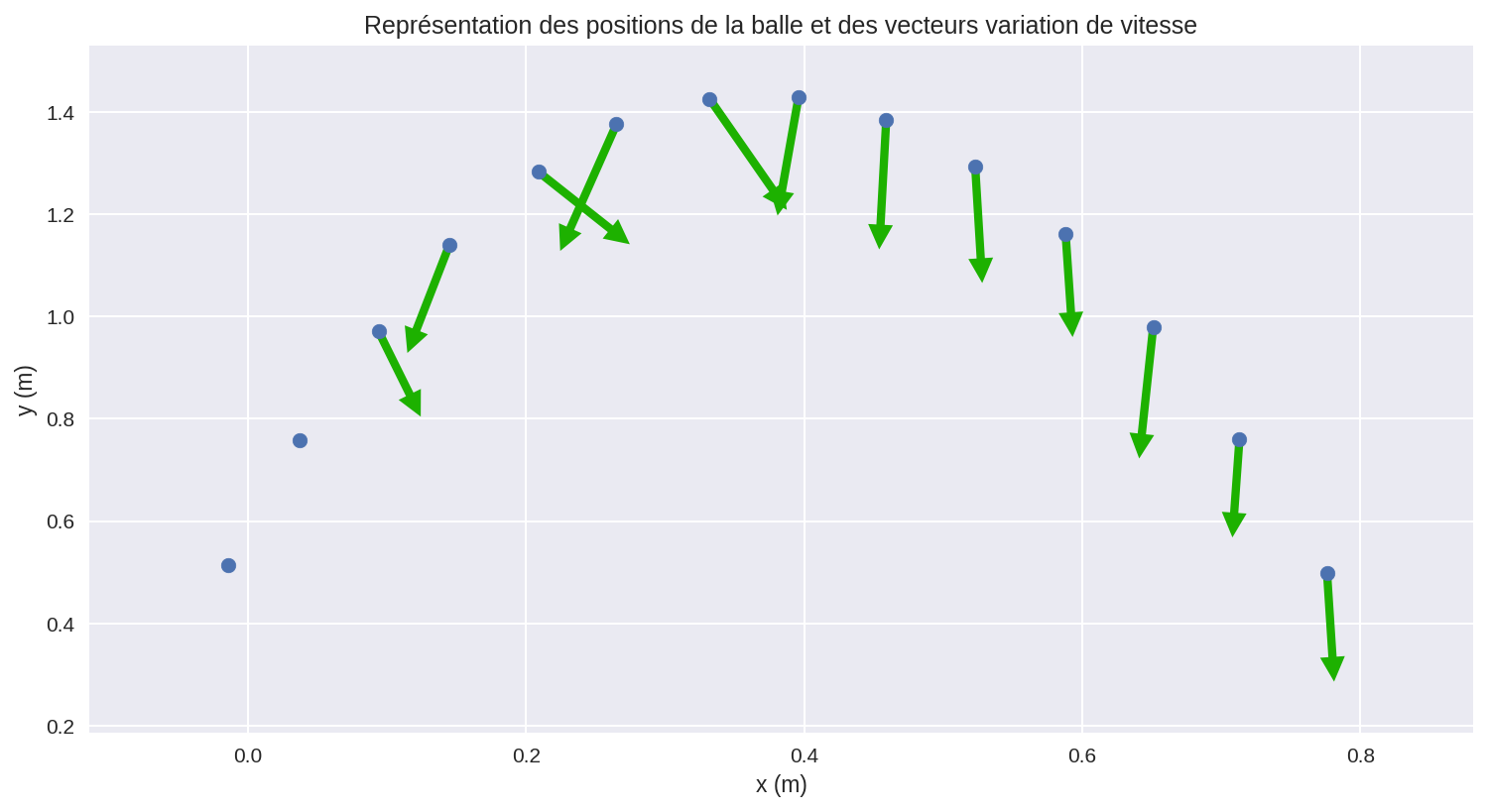
- Que peut-on dire de la résultante des forces dans l’expérience ? Donner son expression.
import math
liste_g = [0 for i in range(N-2)]
for i in range(N-2):
liste_g[i] = math.sqrt(DVx[i]**2+DVy[i]**2) / Dt
print(liste_g)
[9.641873278236918, 10.333128957692269, 8.771796682526544, 10.599996676414328, 9.423496672072481, 10.10361849617323, 9.87144168962349, 9.644605848301204, 9.87411072892867, 10.124461465197355, 9.20852668509259, 10.330578512396672]
- À quoi correspondent les éléments de
liste_g? Donner leur expression littérale.
M = 0
for i in range(N-2):
M += liste_g[i]
print(M / (N-2))
9.827302974387981
- Qu’est calculé dans la cellule précédente. Que cela permet-il de confirmer ?
Théoriquement, nous aurions dû obtenir la figure suivante :
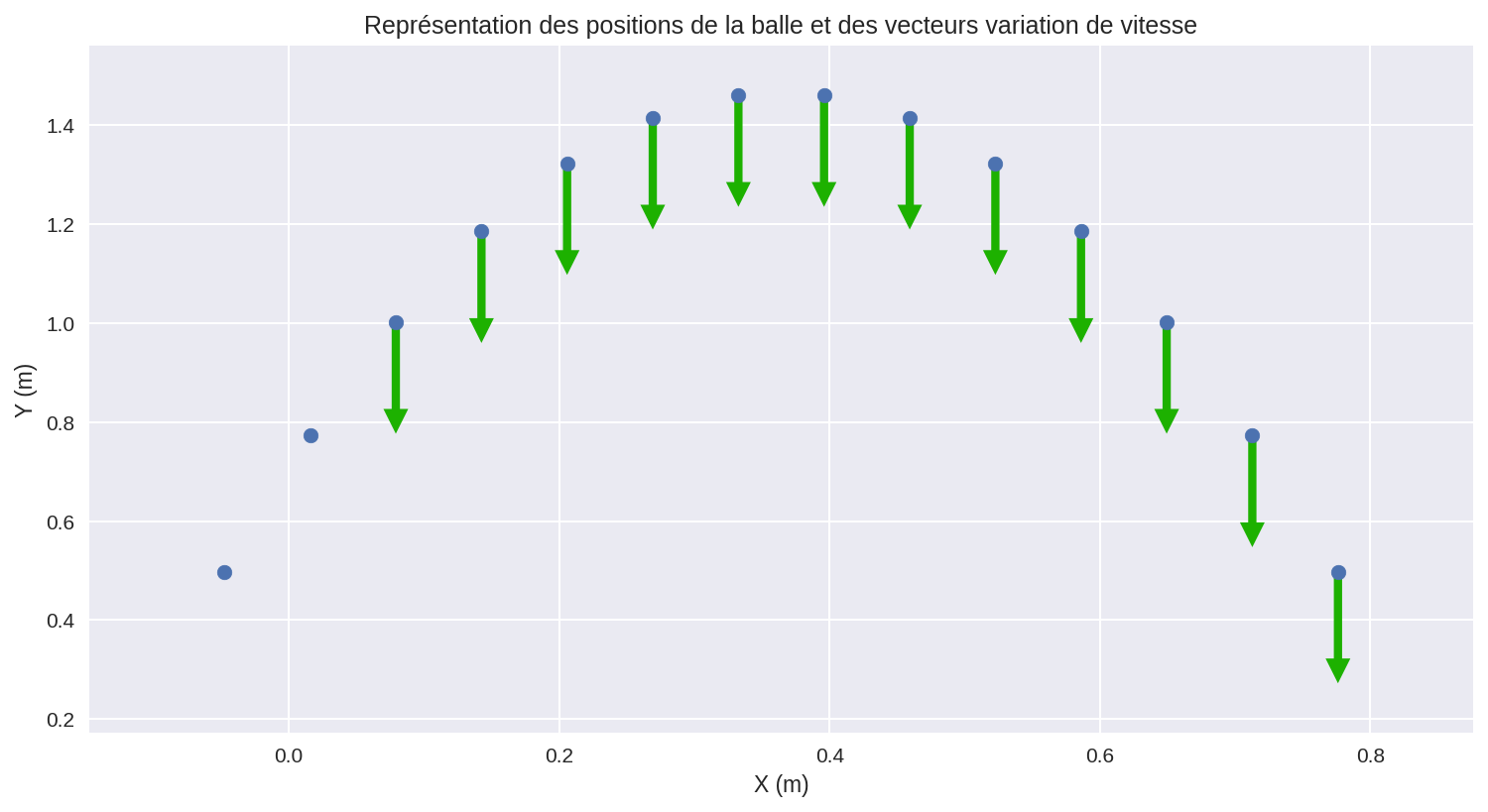
- Pourquoi n’est-ce pas tout à fait le cas selon vous ?