Python

Codes Python présents dans les différentes activités et dans le cours réunis dans le notebook ci-dessous.
Codes à comprendre :
Comment déterminer l’évolution des quantités de matière d’une réaction en fonction de l’avancement ?
import matplotlib.pyplot as plt
## INITIALISATION DES VARIABLES
# coefficients stœchiométrique
# aA A + aB B -> aC C + aD D
aA = 2
aB = 3
aC = 1
aD = 2
# quantités initiales
nA = 0.05
nB = 0.06
nC = 0.01
nD = 0
x = 0 # Initialisation de l'avancement
dx = 0.001 # Incrément d'avancement
X = [x] # Liste stockant les valeurs successives d'avancement
NA = [nA] # Liste stockant les quantités des matières du réactif A
NB = [nB] # Idem pour le réactif B
NC = [nC] # Idem pour le produit C
ND = [nD] # Idem pour le produit D
## COEUR DU PROGRAMME
while NA[-1] > 0 and NB[-1] > 0:
x = x + dx
X.append(x)
NA.append(nA - aA * x)
NB.append(nB - aB * x)
NC.append(nC + aC * x)
ND.append(nD + aD * x)
## TRACÉS ET PRINT DES QUANTITÉ FINALES
plt.figure(figsize=(15,10),dpi=150)
plt.plot(X, NA, label='nA')
plt.plot(X, NB, label='nB')
plt.plot(X, NC, label='nC')
plt.plot(X, ND, label='nD')
plt.grid(True)
plt.xlabel('x (mol)')
plt.ylabel('n (mol)')
plt.legend()
plt.show()
## PRINT DES QUANTITÉ FINALES
print(f"\nL'avancement final vaut xmax = {x:.1E} mol")
if NA[-1] > 0:
print("Le réactif limitant est B")
NB[-1]=0
elif NB[-1] > 0:
print("Le réactif limitant est A")
NA[-1]=0
else:
print("Le mélange est stœchiométrique")
NA[-1]=NB[-1]=0
print(f"Quantités finales :\n\
NA = {NA[-1]:.1E} mol\n\
NB = {NB[-1]:.1E} mol\n\
NC = {NC[-1]:.1E} mol\n\
ND = {ND[-1]:.1E} mol\n")
Seule la boucle while est à comprendre.
while NA[-1] > 0 and NB[-1] > 0: signifie qu’on continue à retourner dans la boucle tant qu’il reste des réactifs.
En effet, NA et NB sont respectivement les listes des quantités de matière du réactif A et du réactif B obtenues pour chaque valeur de l’avancement x. NA[-1] et NB[-1] correspondent aux dernières valeurs ajoutées dans chacune des listes, celles ajoutées au dernier tour de boucle ([-1] permet de récupérer la dernière valeur d’une liste).
Donc tant qu’il reste des réactifs, on continue à faire ce qu’il y a dans la boucle, c’est-à-dire augmenter l’avancement x de la petite valeur dx, puis ajouter la nouvelle valeur correspondante aux listes des quantités de matière des réactif et des produits. Cela revient finalement à ajouter une nouvelle ligne au tableau d’avancement à chaque tour de boucle !
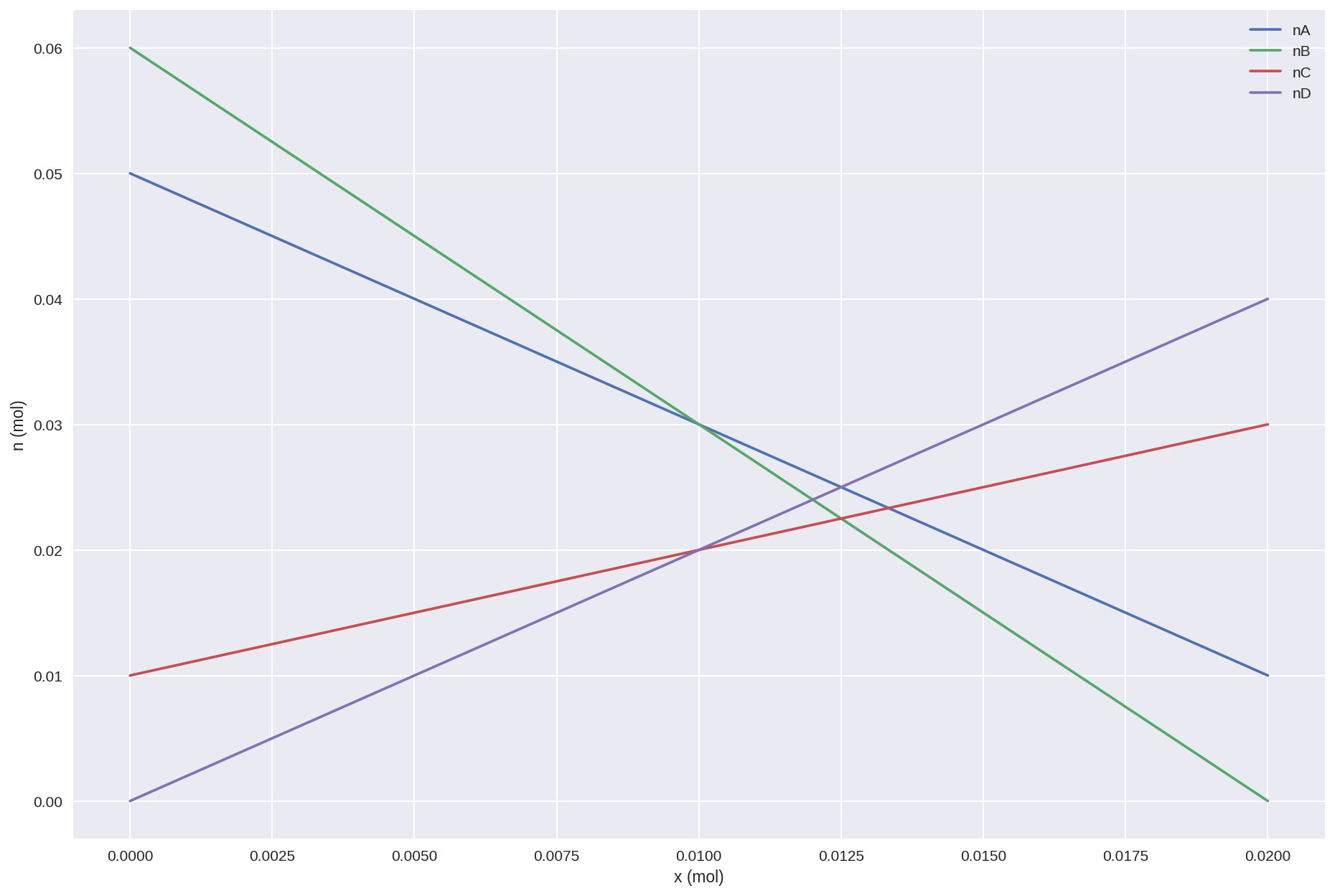
L'avancement final vaut xmax = 2.0E-02 mol
Le réactif limitant est B
Quantités finales :
NA = 1.0E-02 mol
NB = 0.0E+00 mol
NC = 3.0E-02 mol
ND = 4.0E-02 mol
Création d’une liste des vitesses et d’une liste des variations de vitesse à partir d’une liste de positions.
import matplotlib.pyplot as plt
# Création de la liste des abscisses et de la liste des ordonnées
ListePoints=[(-2.73, 1.53),(-1.21, 3.12),(0.56, 4.29),(2.22, 4.63),(3.67, 4.24),(4.85, 3.28),(5.69, 1.88),(6.13, 0.19),(6.11, -1.63),(5.69, -3.29),(5.08, -4.32),(4.47, -4.29),(3.9, -3.26),(3.28, -1.77),(2.5, -0.38),(1.45, 0.4),(0.17, 0.58),(-1.27, 0.36),(-2.78, -0.06)]
N = len(ListePoints)
X,Y = zip(*ListePoints)
X,Y = list(X),list(Y)
dt = 1/10
# Création de la liste des vecteurs vitesse :
Vx = []
Vy = []
for i in range(N-1):
Vx.append((X[i+1]-X[i])/dt)
Vy.append((Y[i+1]-Y[i])/dt)
# Positions des extrémités des vecteurs :
echelle = 1/15 # permet d'ajuster la taille des vecteurs
finVx = [X[i] + Vx[i]*echelle for i in range(N-1)]
finVy = [Y[i] + Vy[i]*echelle for i in range(N-1)]
# Tracés :
plt.figure(figsize=(15,15),dpi=150)
plt.scatter(X, Y, zorder=2)
for i in range(N-1):
plt.annotate('', xy=(finVx[i], finVy[i]), xytext=(X[i], Y[i]), arrowprops=dict(facecolor='#FFD932',edgecolor='#FEAE00'), zorder=1)
plt.text(X[i] + Vx[i]*echelle - 0.1, Y[i] + Vy[i]*echelle + Vy[i]/abs(Vy[i])*0.1, f'{(Vx[i]**2+Vy[i]**2)**0.5:.1f} m/s', fontsize=9, color='#FEAE00')
plt.title('Représentation des positions et des vecteurs vitesse', fontsize=20)
plt.xlim(min(X+finVx)-0.1, max(X+finVx)+0.1)
plt.ylim(min(Y+finVy)-0.1, max(Y+finVy)+0.1)
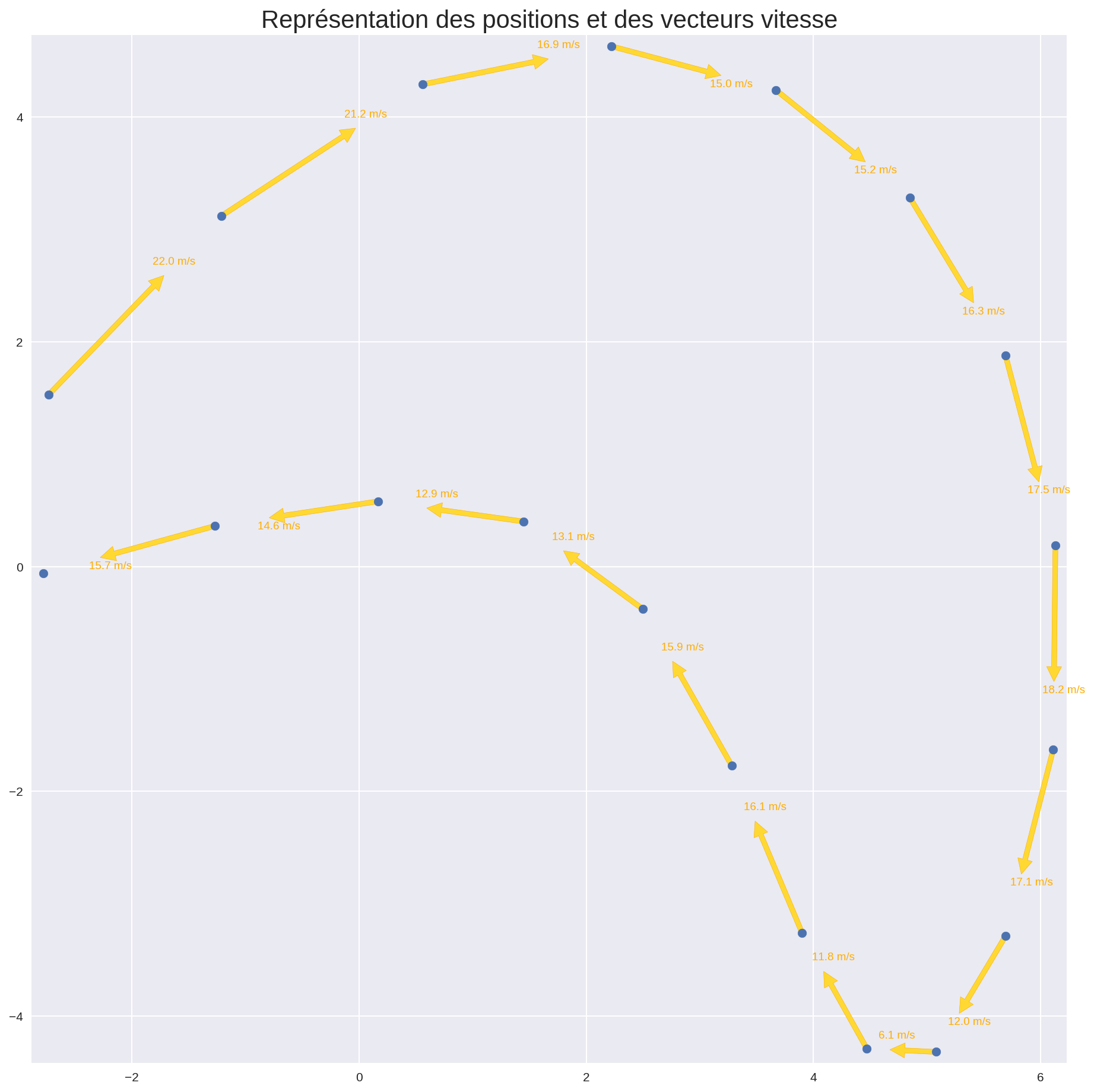
La seule partie à comprendre est la construction des listes des deux composantes de la vitesse (on suppose ici un mouvement dans un plan) :
Vx = []
Vy = []
for i in range(N-1):
Vx.append((X[i+1]-X[i])/dt)
Vy.append((Y[i+1]-Y[i])/dt)
En particulier, il faut retenir qu’on doit arrêter la boucle avant le dernier point (N-1 plutôt que N) car sinon le calcul lèverait une erreur puisqu’on essaierait alors de calculer la vitesse du dernier point à partir du point d’après qui n’existe pas.
Rq : la méthode L.append(e) ajoute l’élément e à la liste L.
On crée les vecteurs variation de vitesse sur le même modèle :
# Création de la liste des vecteurs vitesse :
DVx = []
DVy = []
for i in range(N-2):
DVx.append(Vx[i+1]-Vx[i])
DVy.append(Vy[i+1]-Vy[i])
# Positions des extrémités des vecteurs :
echelle = 1/15 # permet d'ajuster la taille des vecteurs
finDVx = [X[i] + DVx[i]*echelle for i in range(N-2)]
finDVy = [Y[i] + DVy[i]*echelle for i in range(N-2)]
# Tracés :
plt.figure(figsize=(15,15),dpi=150)
plt.scatter(X, Y, zorder=2)
for i in range(N-2):
plt.annotate('',
xy=(finDVx[i], finDVy[i]),
xytext=(X[i], Y[i]),
arrowprops=dict(facecolor='#1DB100',edgecolor='#017100'), zorder=1)
plt.text(X[i] + DVx[i]*echelle - 0.1,
Y[i] + DVy[i]*echelle + DVy[i]/abs(DVy[i])*0.1,
f'{(DVx[i]**2+DVy[i]**2)**0.5:.1f} m/s', fontsize=9, color='#017100')
plt.title('Représentation des positions et des vecteurs variation de vitesse', fontsize=20)
plt.xlim(min(X+finDVx)-0.1, max(X+finDVx)+0.1)
plt.ylim(min(Y+finDVy)-0.1, max(Y+finDVy)+0.1)
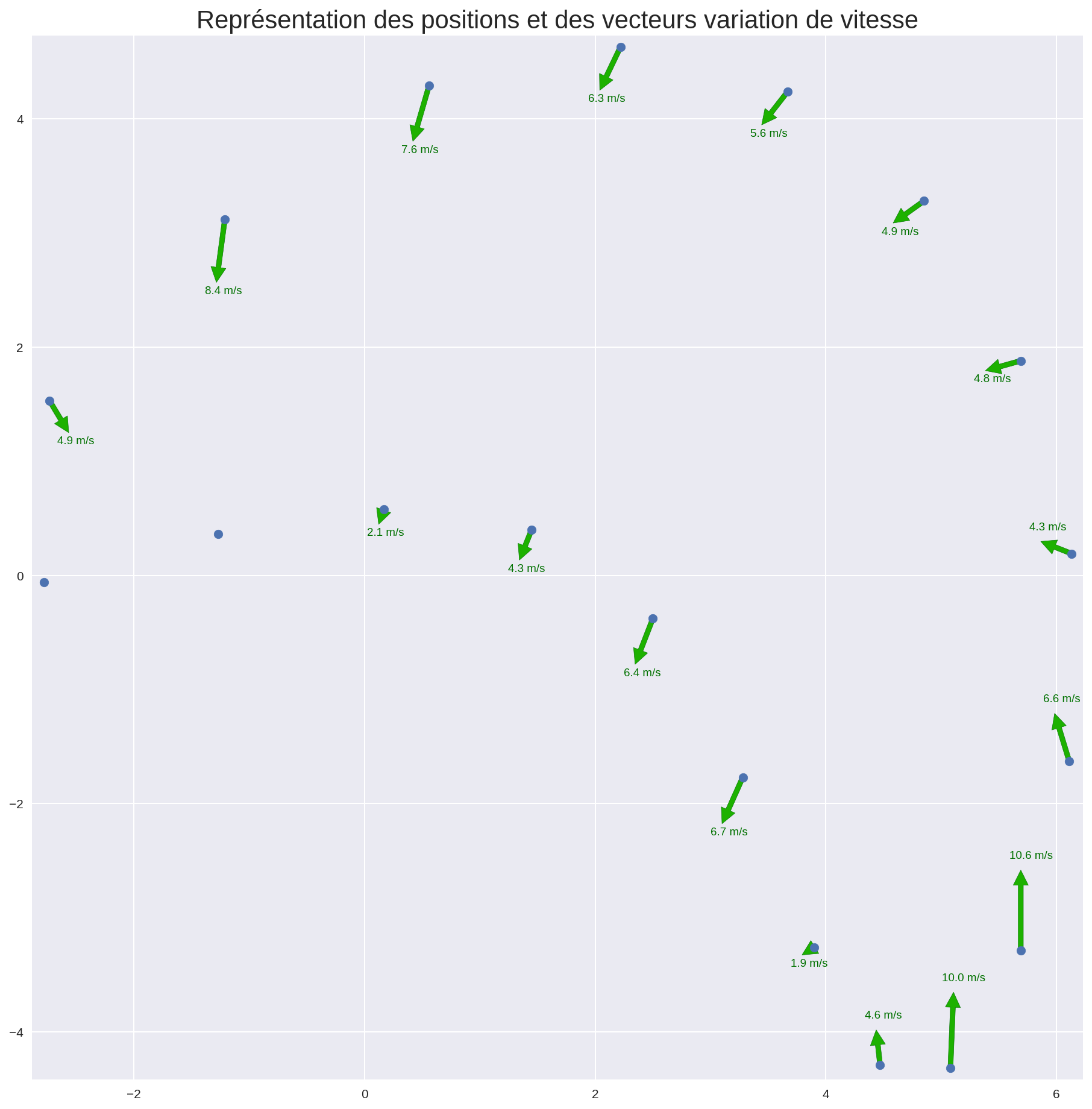
Attention, on s’arrête maintenant avant l’avant dernier point (N-2) puisqu’on n’a pas pu calculer la vitesse du dernier point dans le code précédent.