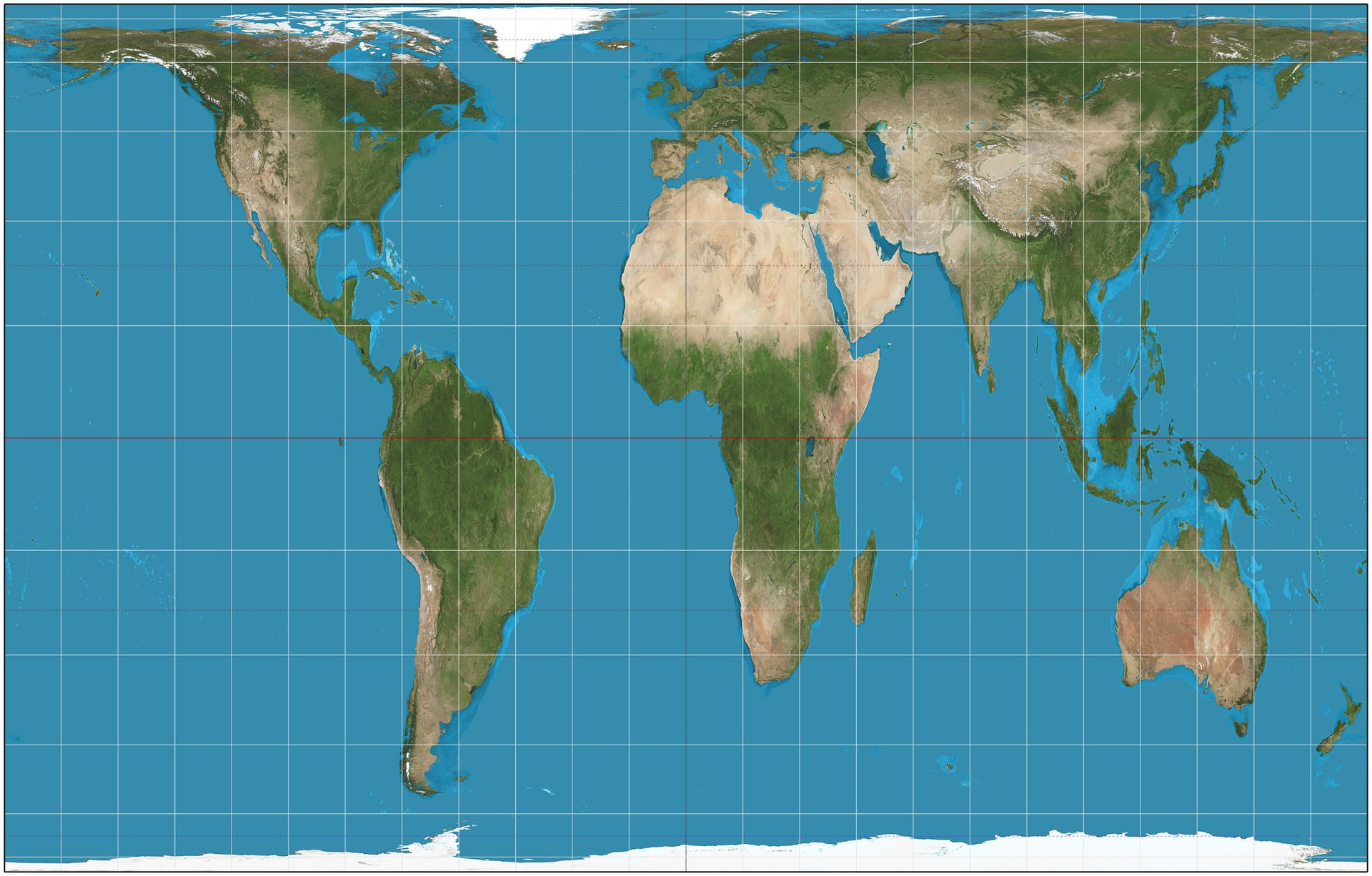
Forme de la Terre
L’auteur de cette vidéo a le mérite d’appliquer en partie une démarche scientifique car c’est dans l’essence même de la science que d’essayer de détruire une théorie par la démonstration de son inconsistance à l’aide d’expériences. On verra cependant que les expériences rapportées sont assez loin de remettre en question la sphéricité de la Terre 🌍… Elles vont malgré tout nous permettre de réfléchir à des points intéressants comme la distance de l’horizon, le calcul d’Ératosthène ou encore le chemin le plus court entre deux points sur une sphère.
C’est quand même dommage que l’école n’ait pas su apporter des réponses aux étonnements de l’auteur (comme la notion de perspective pour expliquer l’apparent non parallèlisme des rayons solaires ou la notion d’inertie pour le rassurer quant à la vitesse du sol terrestre à l’équateur).
Horizon

Jusqu’où peut-on voir ? Pourquoi peut-on parfois voir plus loin ?
Une première activité pour tenter de répondre à ces questions.
Quelques informations sur les mirages.
Ératosthène
Comment un savant de la Grèce Antique a-t-il réussi à déterminer la taille de la Terre avec un bâton ?
Notre ami platiste a raison de dire que le calcul d’Ératosthène ne prouve pas que la Terre est sphérique. Il trouve juste son rayon si elle l’était (et c’est déjà pas mal). Les résultats d’une théorie dépendent complètement du modèle dans lequel la théorie s’inscrit.
À partir des mêmes observations (ombre à Alexandrie mais pas à Syène à midi au solstice d’été) mais des prémisses différentes (un modèle de Terre plate avec un petit Soleil flottant au-dessus), Anaxagore aboutissait ainsi deux siècles avant Ératosthène aux mêmes résultats numériques mais il leur donnait une signification bien différente ; le Soleil serait situé, selon lui, à 6500 km de la Terre.
Une des preuves de la rotondité rapportée par Aristote, l’ombre de la Terre pendant une éclipse de Lune, est bien illustrée sur la superposition de photos ci-dessous (le contraste et la luminosité ont été boostés sur l’image centrale).

Si cette preuve est compatible avec une Terre ronde mais plate, les deux autres (disparition derrière l’horizon et changement de l’élévation des étoiles en fonction de la lattitude) imposent la sphéricité.
Histoire du mètre
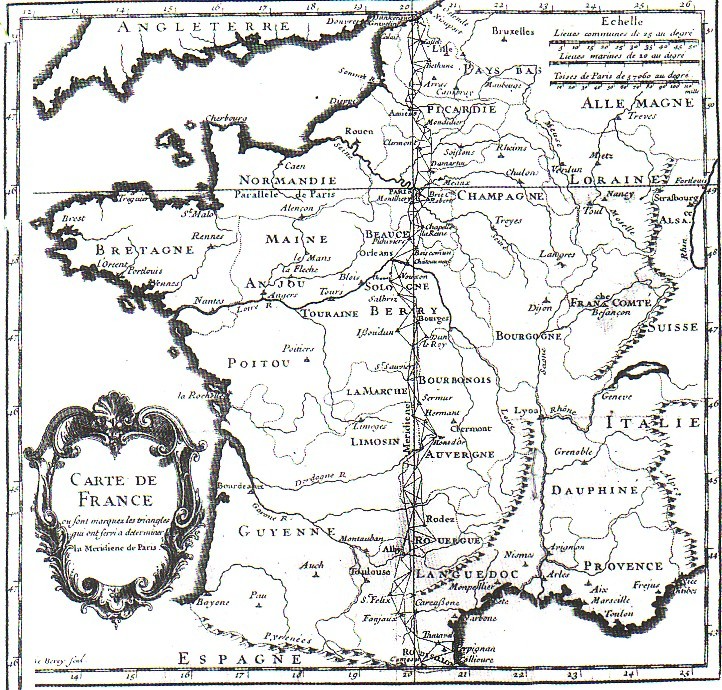
Documentaire sur la naissance du mètre pendant la révolution française.

Se déplacer sur une sphère
Quel est le trajet le plus court entre deux points ?
Dans un espace plat, c’est la droite. Mais ce n’est plus cas si l’espace est courbe !
On le constate dans l’exemple du trajet en avion entre Bordeau et Portland.
Représenter une sphère sur un plan
La projection cartographique est un ensemble de techniques géodésiques (« la science qui mesure et représente la surface terrestre ») permettant de représenter une surface non plane (surface de la Terre, d’un autre corps céleste, du ciel, …) dans son ensemble ou en partie sur la surface plane d’une carte.
L’impossibilité de projeter le globe terrestre sur une surface plane sans distorsion explique que diverses projections aient été inventées, chacune ayant ses avantages.
La projection la plus utilisée est celle de Mercator. Elle a pour avantage d’être conforme, c’est-à-dire qu’elle conserve les angles, ce qui est particulièrement utile aux marins pour calculer un cap. Mais elle déforme les distances et les aires.
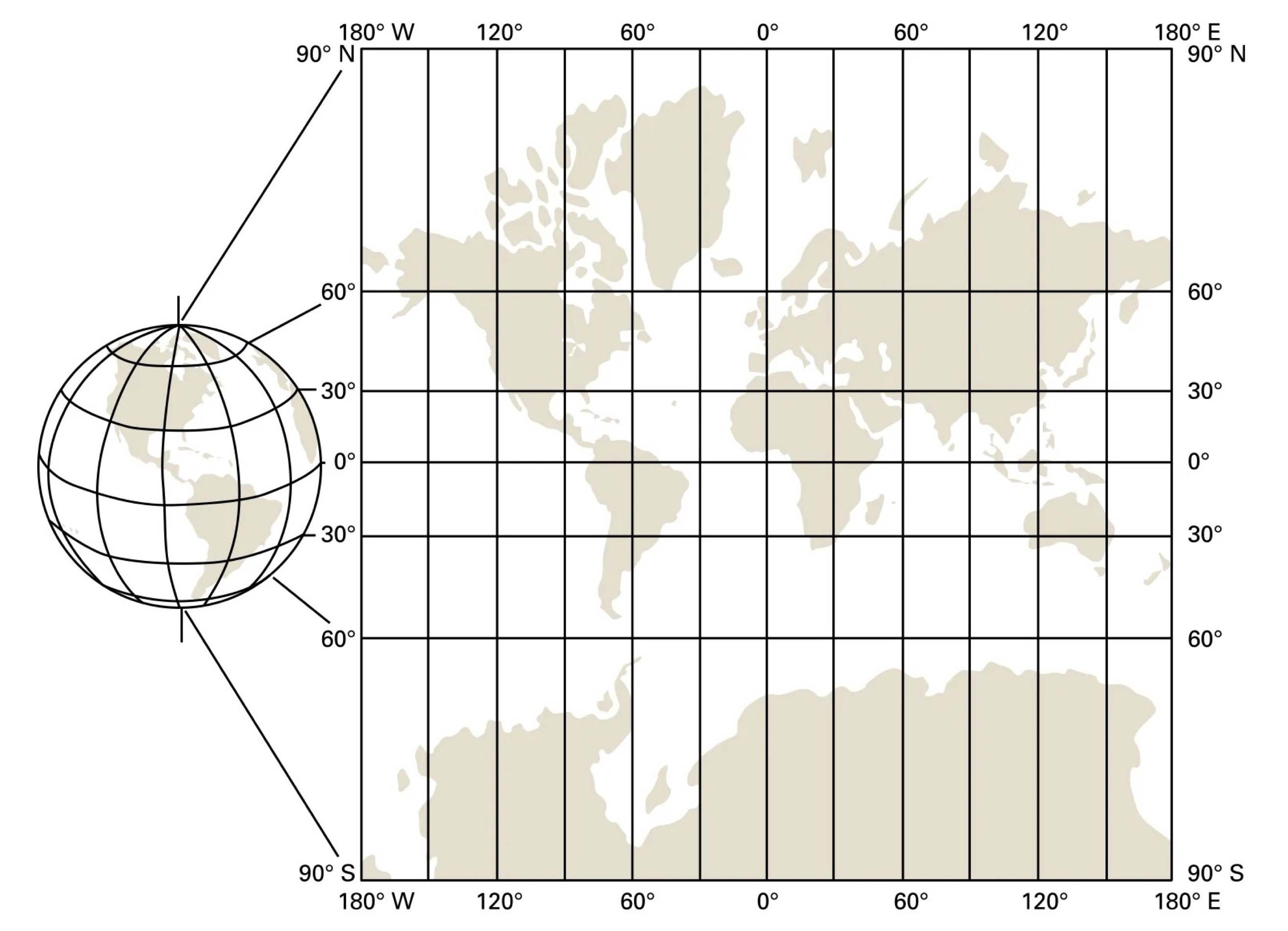
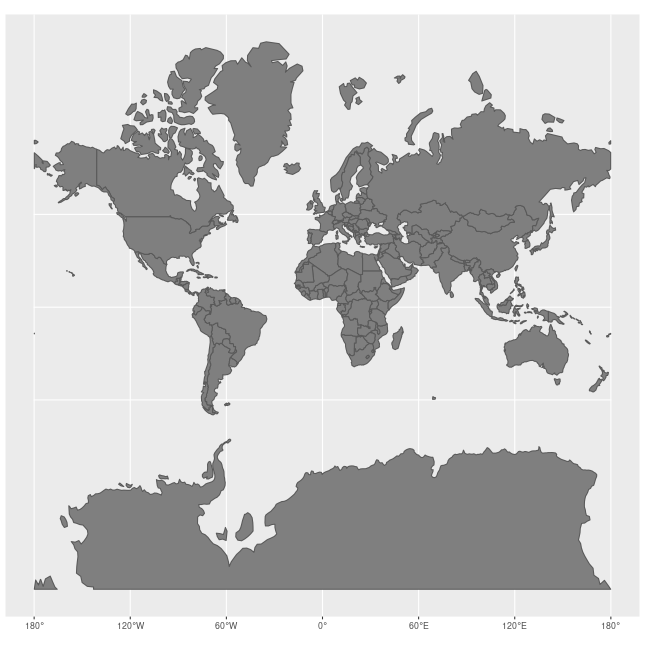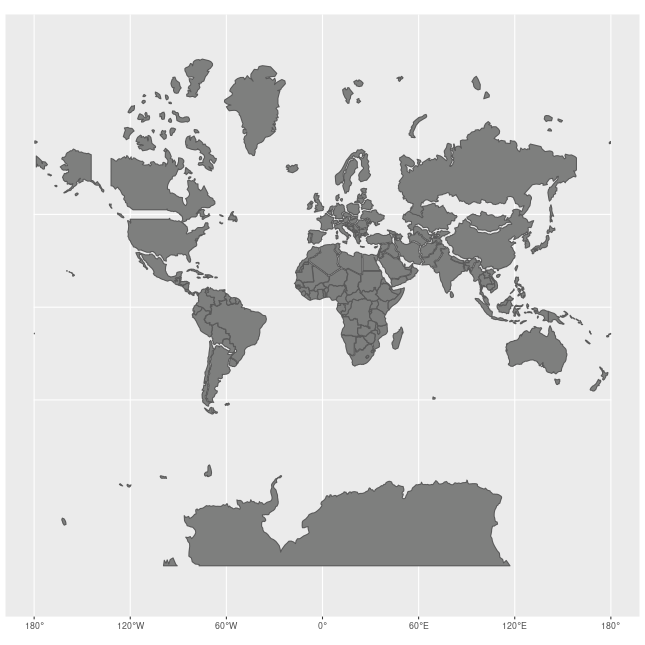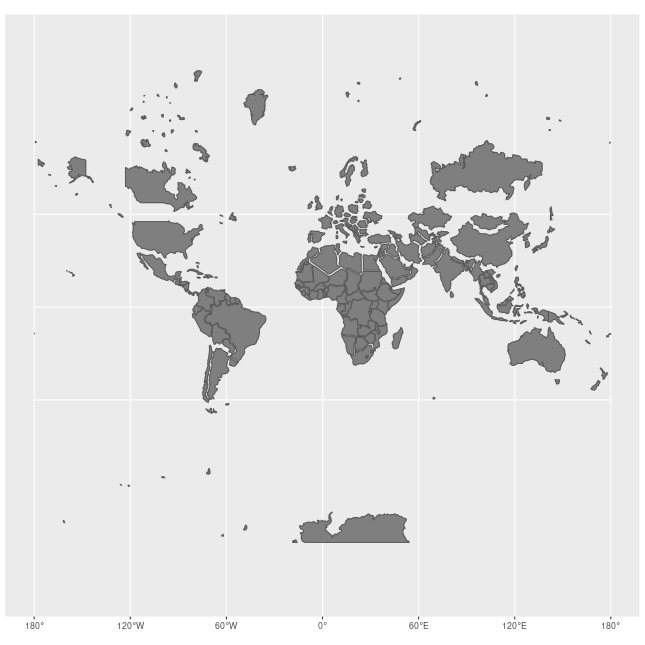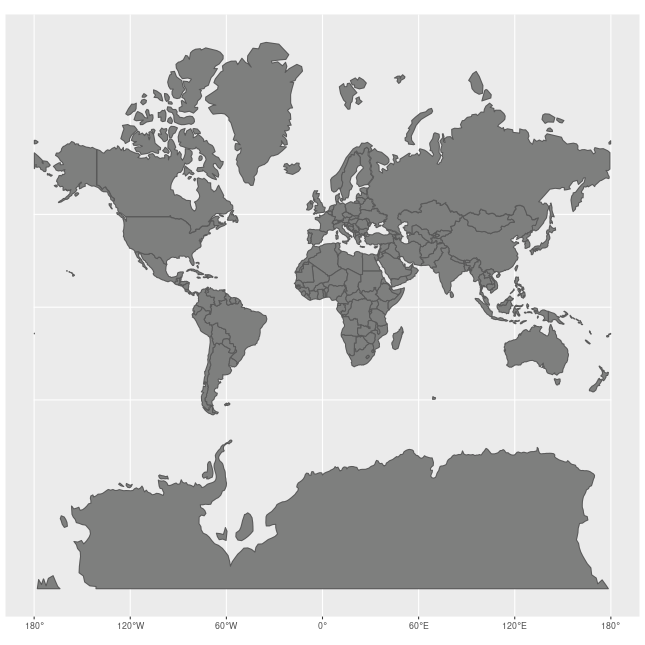
Les cartes intéractives suivantes mettent en lumière ses inconvénients :
- les aires grandissent lorsqu’on s’éloigne de l’équateur
- pareil pour les distances
- La ligne droite n’est pas le trajet le plus court
Pour comparaison, la projection de Peters conserve les aires (mais pas les angles) :