Le son, une information à coder
Analogique vs Numérique
Avant les années 1990, le support sur lequel est enregistrée la musique était le plus souvent analogique, mais avec la démocratisation du Compact Disk, les supports numériques deviennent rapidement majoritaires.
Définir les termes analogique et numérique. Nommer et classer les supports suivants entre analogique et numérique.

Pourquoi numériser ?
Selon vous, quels sont les principaux avantages d’une numérisation des données ?
Correction (cliquer pour afficher)
- permet d'emmagasiner de grandes quantités d'information sur des volumes de faibles dimensions ;
- permet de dupliquer exactement et facilement les informations numériques et cela pour un moindre coût ;
- permet de distribuer largement les informations grâce aux réseaux informatiques et notamment grâce à Internet.
Codage d’un son
Un son est une vibration mécanique se propageant dans l’air ou dans un autre milieu (fluide, solide…). À l’aide d’un micro, un son peut être capté et converti en un signal analogique modélisé mathématiquement par une fonction représentant par exemple une tension en fonction du temps.
Le traitement numérique de ce signal analogique, réalisé à l’aide d’un convertisseur analogique/numérique (CAN), consiste à discrétiser cette fonction en abscisse et en ordonnée pour en extraire un nombre fini de données.
- L’échantillonnage consiste à relever différentes valeurs de la tension à intervalles de temps réguliers.
- La quantification, quant à elle, revient à associer à chaque valeur de l’échantillon un nombre dont la longueur de l’écriture binaire est décidée par avance.
Échantillonnage
Considérons la représentation graphique en fonction du temps de la tension électrique correspondant au signal analogique du La du diapason (La3), son pur de fréquence $f=\pu{440 Hz}$.
Un échantillonnage à la fréquence $f_e$ revient à garder constante la valeur du signal au début de la période pendant toute la période d’échantillonnage $T_e = 1/f_e$.
Plus $f_e$ est grande et plus le signal restitué est fidèle.
Pour quelle valeur de $f_e$, le signal échantillonné est-il un signal carré (ou créneau) ayant la même fréquence que le signal sinusoïdal initial ?
On appelle cette fréquence la fréquence de Nyquist. C’est la fréquence d’échantillonnage minimale nécessaire pour que la fréquence du signal échantillonnée soit la même que celle du signal de départ.
Sachant que l’oreille humaine est capable d’entendre des sons jusqu’à 20000 Hz, à partir de quelle fréquence d’échantillonage est-on sûr d’enregistrer fidèlement un son ?
Sur une ligne téléphonique, un son est échantillonnée à 8000 Hz. Pourquoi est-ce suffisant ?
On considère un ensemble de valeurs obtenues par échantillonnage d’un son pur. L’unité portée sur l’axe des abscisses est la seconde.
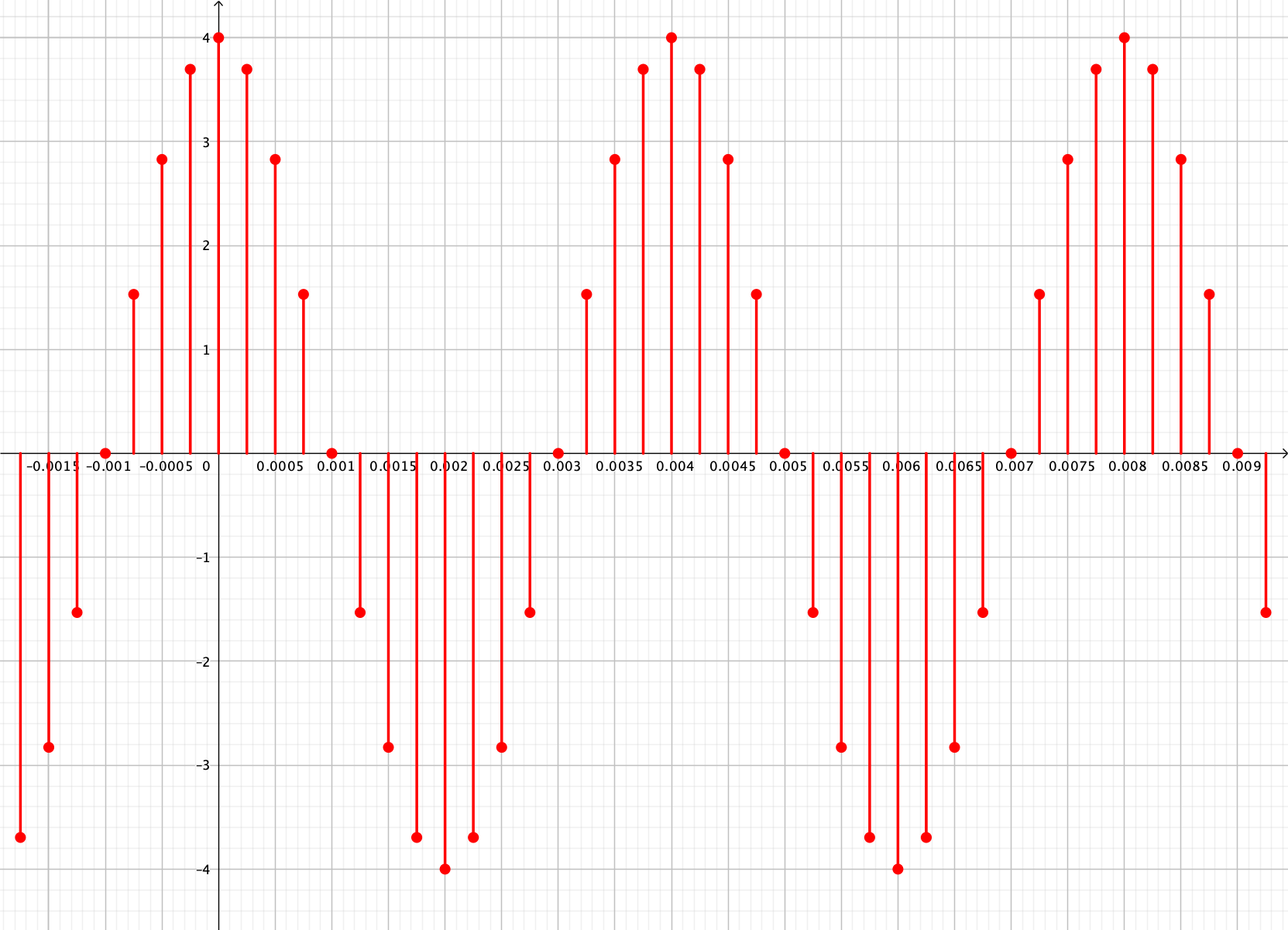
Déterminer la fréquence du son échantillonné.
Déterminer la fréquence $f_e$ d’échantillonnage.
Quantification
Écriture binaire d’un nombre entier
Les shadoks comptent en base 4, mais les ordinateurs, eux, préfèrent la base 2 car ils n’ont que deux chiffres à leur disposition : $1$ et $0$, ouvert ou fermé (un ordinateur n’est finalement qu’un ensemble d’interrupteurs !).
0 et 1 sont les seuls nombres que l’on peut coder sur un seul bit. Sur deux bits, il y a quatre nombres codés : $00$, $01$, $10$ et $11$.
Plus généralement, si $p$ est un entier naturel non nul, on peut coder $2^p$ nombres entiers sur $p$ bits.
| Nombre $p$ de bits | 1 | 2 | 3 | 4 | 8 | 10 | 16 | 24 |
|---|---|---|---|---|---|---|---|---|
| Nombre de nombres codables | 2 | 4 | 8 | 16 | 256 | 1 024 | 65 536 | 16 777 216 |
On voit ainsi qu’un octet, constitué de 8 bits, permet de représenter 256 nombres distincts. L’octet est l’unité qui permet de mesurer la quantité de données en informatique, c’est l’unité de mémoire.
Les nombres positifs sont simplement écrits dans leur écriture binaire : ainsi le nombre 3 a-t-il pour écriture binaire $011$ sur 3 bits.
La technique du complément à 2 permet de coder des nombres négatifs. Si l’espace de codage est de $p$ bits, alors cette technique permet de coder tous les nombres positifs de $0$ à $2^{p-1}$ et tous les nombres négatifs de $-2^p$ à $0$.
Algorithme à suivre :
-
On considère l’écriture binaire de sa valeur absolue. Par exemple pour écrire $-3$ sur 3 bits, on commence par écrire $011$.
-
On détermine le complément à 2 de ce dernier nombre, ce qui revient à prendre la négation de chaque bit : $0$ est remplacé par $1$ et $1$ est remplacé par $0$. Par exemple, $011$ devient $100$.
-
On ajoute $1$ au nombre obtenu (ne pas oublier les retenues éventuelles), ce qui constitue le code cherché. Par exemple, en ajoutant $1$ à $100$, on obtient $101$. Le codage de $-3$ est $101$.
Appliquer l’algorithme ci-dessus pour déterminer le codage de -1 et -2.
Signal numérisé
La courbe ci-dessous est obtenue après quantification de la courbe échantillonnée précédente.
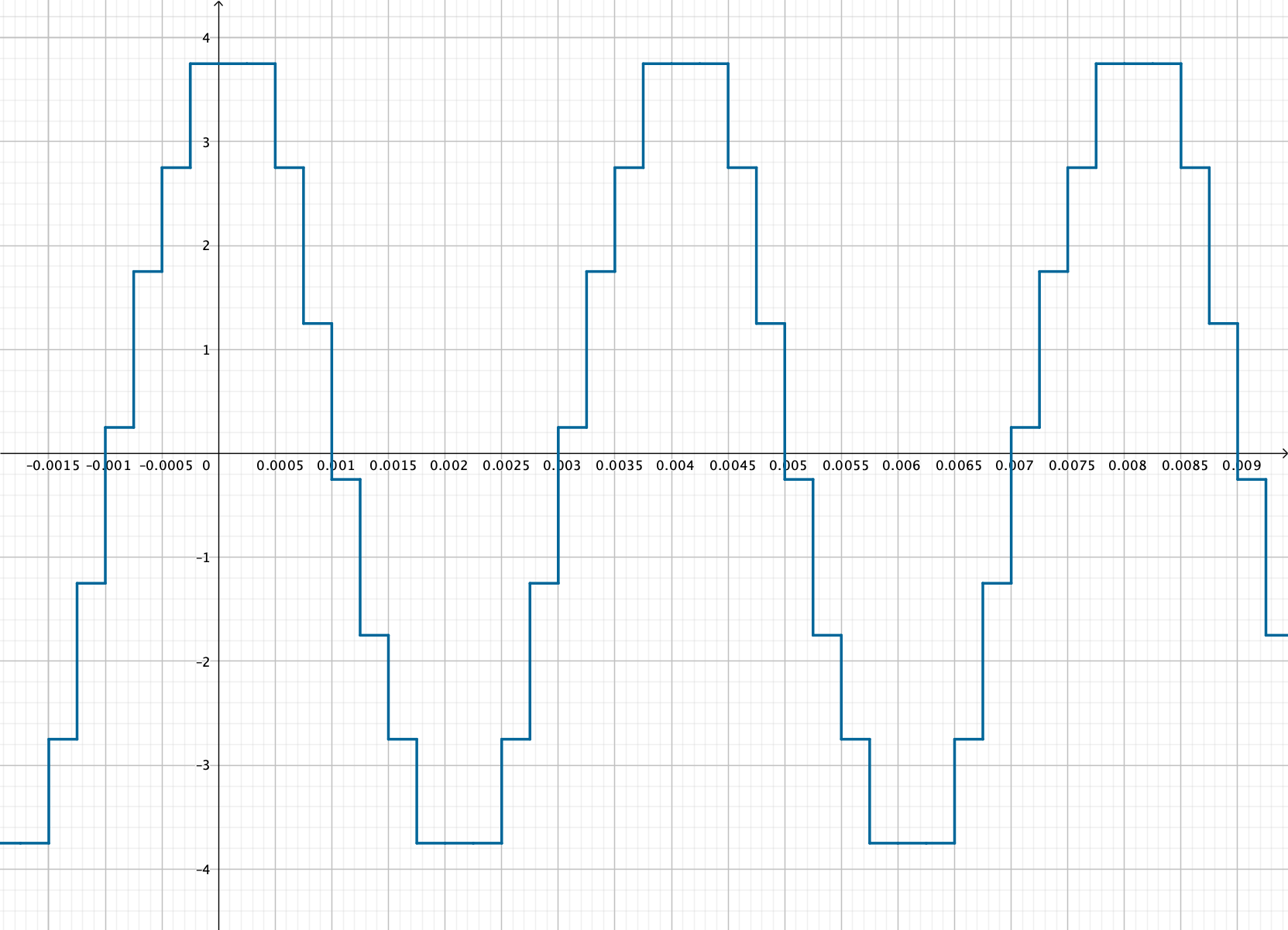
Indiquer sur combien de bits sont codés les valeurs quantifiés.
Exemple :
Fichier sonore original (quantification sur 16 bits et échantillonnage de 48 kHz) :
- Modification de la fréquence d’échantillonnage (en gardant la quantification sur 16 bit) :
| 16 kHz | 8 kHz | 4 kHz | 2 kHz |
|---|---|---|---|
- Modification de la quantification (en gardant l’échantillonnage à 48 kHz) :
| 8 bit | 6 bit | 4 bit | 2 bit |
|---|---|---|---|
Passage par ligne téléphonique (quantification sur 8 bit et échantillonage à 8 kHz) :
Débit binaire et compression
Le débit binaire mesure la quantité de données numériques transmises par unité de temps. L’unité utilisée est le bit par seconde (bit/s) et ses multiples kbit/s, Mbit/s ou Gbit/s.
Quelques débits binaires typiques :
- télégraphie morse : 40 bit/s
- connexion bluetooth : 3 Mbit/s
- connexion internet par fibre : de 100 Mbit/s à 2 Gbit/s
Pour transmettre une voix sur une ligne téléphonique, celle-ci est échantillonnée avec une fréquence de 8000 Hz et est codée sur 8 bits.
Quel débit nécessite la diffusion d’un son sur une ligne téléphonique (en bit/s) ?
Sur un disque audio numérique (CD), la musique est enregistrée en stéréo. Elle est codée sur 16 bits avec une fréquence d’échantillonnage de 44,1 kHz.
Quel espace de stockage (en octets) nécessite une seconde de musique sur un CD ?
Les services de musique en ligne proposent en téléchargement de la musique en diverses résolutions. L’un d’eux propose des fichiers « haute résolution » correspondant à un échantillonnage à 192 kHz, un codage sur 24 bits et un enregistrement stéréo. On fait l’hypothèse que les fichiers proposés ne sont pas compressés.
Quel est l’espace de stockage nécessaire (en octets) pour enregistrer une seconde de musique de cette qualité ? Une connexion ADSL à 8 Mbit/s est-elle suffisante pour pouvoir streamer cet album ? Quelle est la taille d’un fichier pouvant contenir un enregistrement de cette qualité des six suites pour violoncelle de Bach, d’une durée totale de 2 h 15 min ?
Pour réduire les difficultés liées au stockage et à la transmission de fichiers audio, on effectue des compressions des données. Il existe des techniques de compression sans perte et d’autres avec perte.
Une compression est dite sans perte d’information si elle permet de récupérer, après décompression, l’intégralité des sons produits. Elle est réalisée par des algorithmes exploitant les redondances et la prévision de ces redondances dans les fichiers audio. Ainsi, le format FLAC permet de réduire de 30 % à 70 % la taille d’un fichier audio sans perte d’information.
Dans le cas contraire, la compression est dite avec perte. La compression avec perte supprime les sons peu audibles. La compression est effectuée par des algorithmes. Un format très connu de compression de ce type est le MP3.
Les services de musique en ligne proposent en streaming ou en téléchargement des fichiers MP3 à 128 kbit/s. Cela signifie que, pour un tel fichier, une seconde de musique nécessite 128 kbit de données.
Comme pour un CD audio, une seconde de musique nécessite 1411 kbit de données, on en déduit que le taux de compression d’un CD audio vers un fichier MP3 à 128 kbit/s est égal à $\frac{128}{1411}\approx0,091$.
Le taux de compression est alors d’environ 9 % ou encore dans le ratio de 1:11 puisque $0,9\approx1/11$.
Le fichier audio précédent contenant les suites de Bach est compressé en un fichier MP3 à 320 kbit/s. Calculer le taux de compression pour passer d’un fichier à l’autre. Quelle est la taille du fichier MP3 obtenu ? Un mélomane possède dans son audiothèque de nombreux CD, tous enregistrés en stéréo, échantillonnés à 44,1 kHz et codés sur 16 bits. Il estime qu’en moyenne, chaque CD dure une heure et décide de stocker sa musique sous forme de fichiers MP3 à 320 kbit/s. Combien peut-il stocker de fichiers MP3 sur un disque dur ayant une capacité de 1 To ?