Son et musique
Le son, un phénomène vibratoire
Le son est une vibration qui se déplace de proche en proche dans un milieu matériel.
Joseph Fourier (1768-1830) a montré que tout signal périodique peut se décomposer en une somme de sinusoïdes.
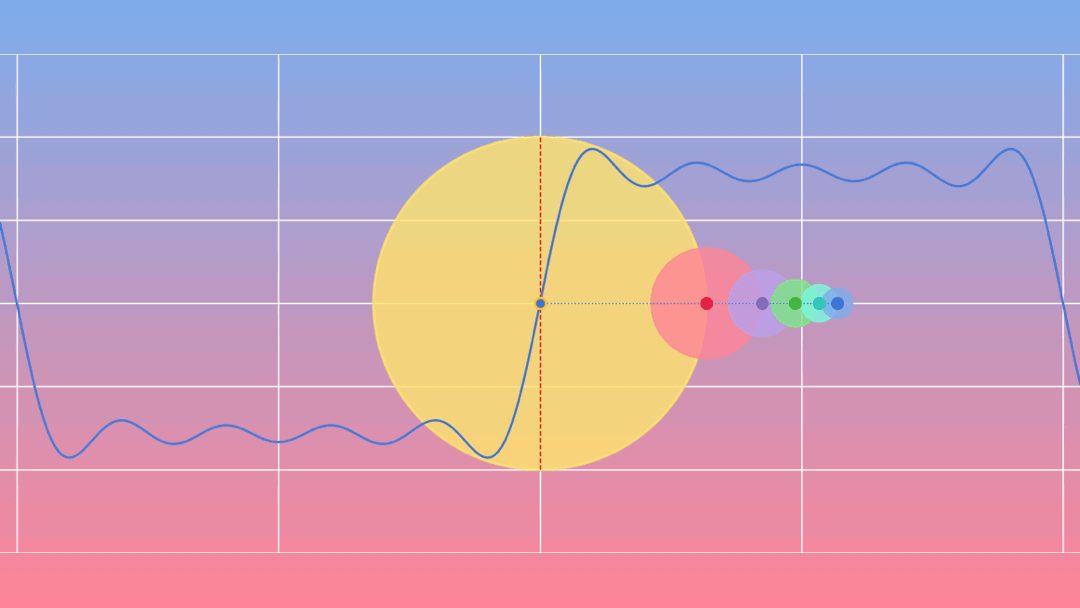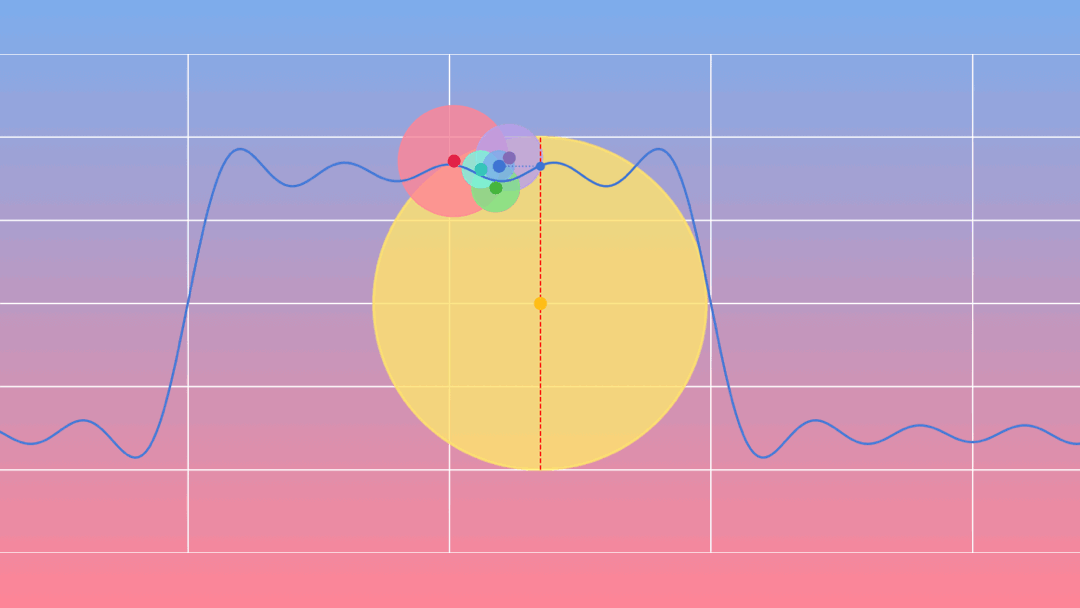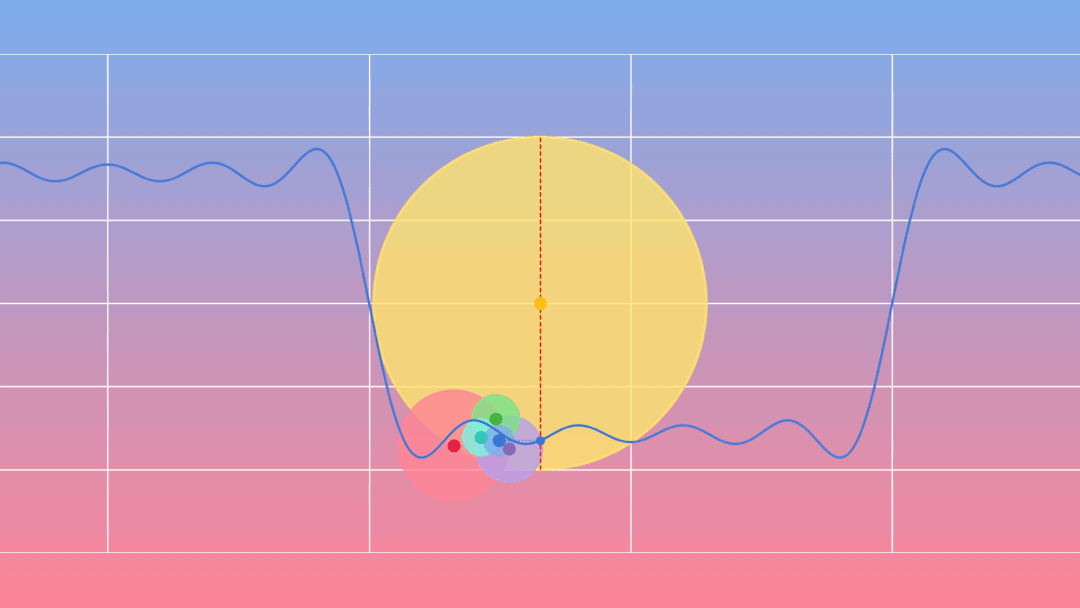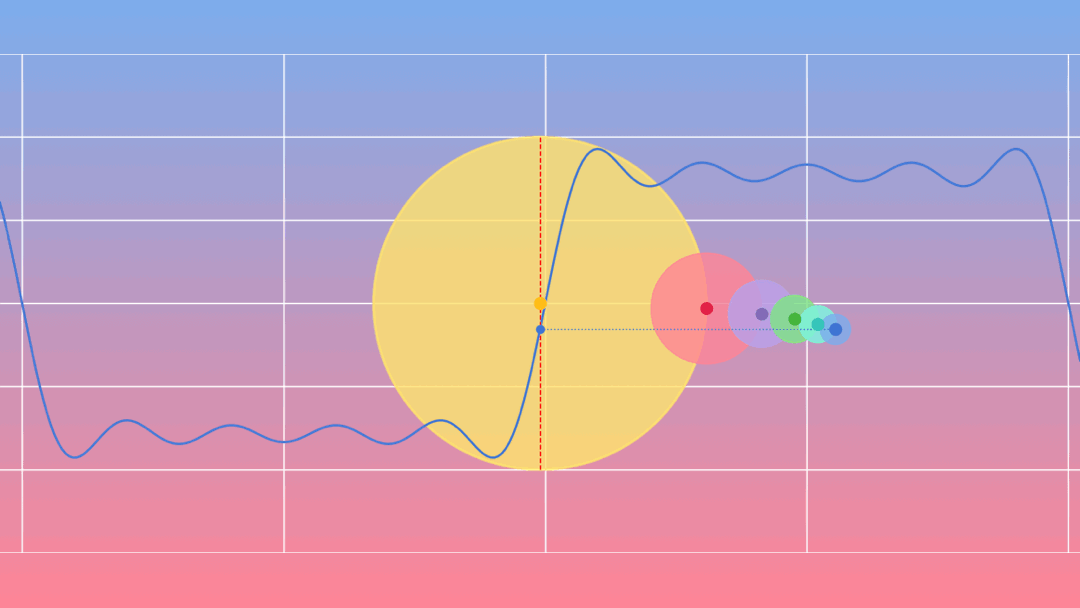
La musique ou l’art de faire entendre les nombres
Son pur et son composé
Un son pur est une vibration sinusoïdale. C’est un signal ne contenant qu’une seule fréquence.
Le son correspondant à une note jouée par un instrument de musique n’est pas un son pur, mais le signal sonore $s$ qui lui est associé a la particularité d’être périodique ($s(t+T)=s(t)$ où $T=1/f$ est la période du signal et $f$ sa fréquence, exprimée en hertz). On parle de son composé.
Un son composé (représenté par une fonction périodique) résulte de la combinaison de sons purs (associés à des sinusoïdes) dont les fréquences sont toutes multiples de l’une d’elles, appelée la fréquence fondamentale. La fréquence fondamentale $f$ est perçue par l’oreille comme étant la fréquence du son. C’est pourquoi elle est encore appelée hauteur du son. L’ensemble des fréquences $f$, $2f$, $3f$,.. et des amplitudes associées constitue le spectre du son.
Produire des notes
Pour la plupart des instruments, les différentes fréquences d’un son musical naissent des différentes possibilités qu’une onde a de résonner dans une cavité de longueur donnée. C’est ainsi que le registre d’un instrument dépend de sa taille.

La cavité résonnante peut être une colonne d’air comme dans les instruments à vent ou une corde comme dans les instruments… à cordes.
Dans le cas d’une corde, deux autres paramètres que la longueur permettent de joueur sur la hauteur du son (activité corde).
Consonance
Dans l’applet suivant, la note bleue est un La. Essayez, en déplaçant la fréquence de la note rouge, de trouver une note qui “sonne” de manière tellement similaire à la note bleue qu’on a envie de l’appeler La elle aussi. Pour trouver une critère “physique” de proximité, vous pourrez vous aider du phénomène qu’on obtient lorsque les deux notes ont une fréquence très proche.
La décomposition d’un son composé en somme de sons purs de fréquences multiples de la fréquence fondamentale permet d’expliquer pourquoi certains sons produits simultanément sont agréables à l’oreille ; on dit alors qu’ils sont consonants.
Plus les spectres de deux sons ont de fréquences en commun, et plus il apparaissent consonants.
On remarque que le meilleur recouvrement est obtenu lorsque le fondamental du deuxième son a une fréquence double ou moitié par rapport au fondamental du premier son (une fréquence sur deux du spectre est commune).
Le deuxième son est alors dit à l’octave par rapport au premier.
Les deux notes sont considérées comme identiques.
L’oreille humaine est capable de percevoir des sons dont la fréquence est comprise entre 20 Hz et 20 000 Hz. Déterminer le nombre de Do différents audibles par l’oreille humaine sachant que la hauteur (fréquence) du Do 0 est de 33 Hz.
La note la plus basse d’un piano a une fréquence de 27,5 Hz et la note la plus haute a une fréquence d’environ 4 186 Hz. Combien y a-t-il d’octaves dans un piano ?
Si le fondamental du deuxième son a une fréquence triple par rapport au premier (ou ×1,5 en ramenant à l’octave précédent), on recouvre une fréquence sur trois. La note du deuxième son correspond alors à la quinte de la note du premier son.
Ce son est suffisamment différent pour que la note puisse être considérée comme distincte de la première.
Cycle des quintes
On a jusque là deux notes : la note de départ et sa quinte. Comment en obtenir de nouvelles ?
Il suffit de prendre la quinte de la quinte, puis la quinte de la quinte de la quinte, etc.
À chaque fois, on obtient la quinte en multipliant la fréquence de la note précédente par 3 et pour garder toutes nos notes à l’intérieur d’une même octave, on divise autant de fois que nécessaire par 2 pour que la fréquence finisse dans l’intervalle $[f_1,2f_1]$ où $f_1$ est la fréquence de la note 1.
Finalement chaque nouvelle note sera de la forme $f_1\times\frac{3^m}{2^n}$.
Un algorithme permettant d’obtenir les différentes notes est donné par le diagramme ci-dessous.
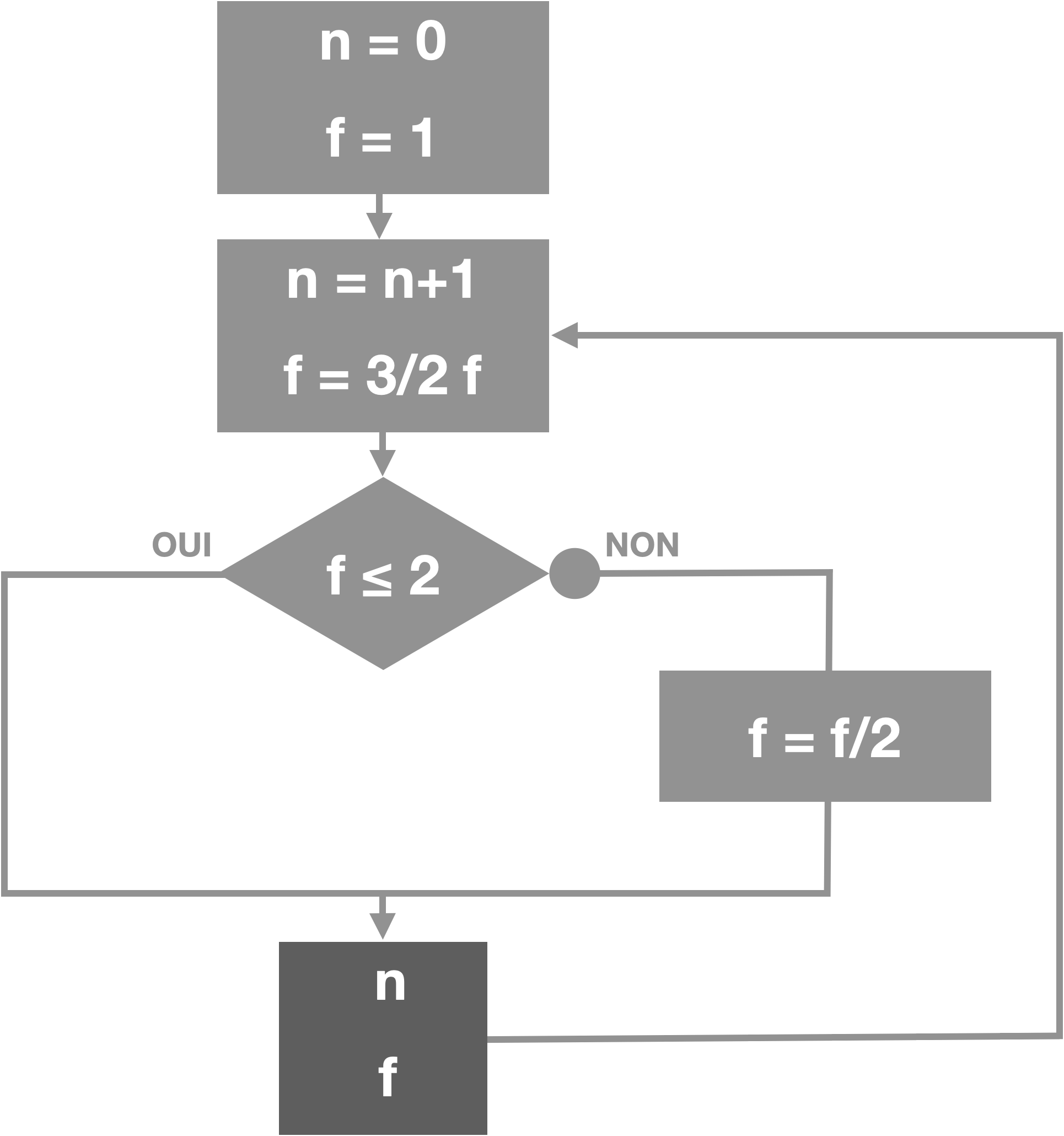
Compléter l’implémentation Python ci-dessous donnant les 55 premières notes obtenues en complétant les pointillés.
Lorsqu’une note obtenue est proche d’une note déjà présente, on peut “refermer” la gamme en ne gardant que les notes obtenues jusque là. On construit ainsi la gamme de Pythagore.
On remarque ainsi que la $12^e$ note correspond approximativement à la note de départ ($f=1$).
En effet : $3^{12}\approx 2^{19}$. On dit alors que le cycle des quintes reboucle (même si imparfaitement) incitant à découper l’octave en 12 notes.
Presque tous les instruments occidentaux sont construits pour pouvoir reproduire la gamme chromatique faite de 12 notes séparées par des demi-tons.
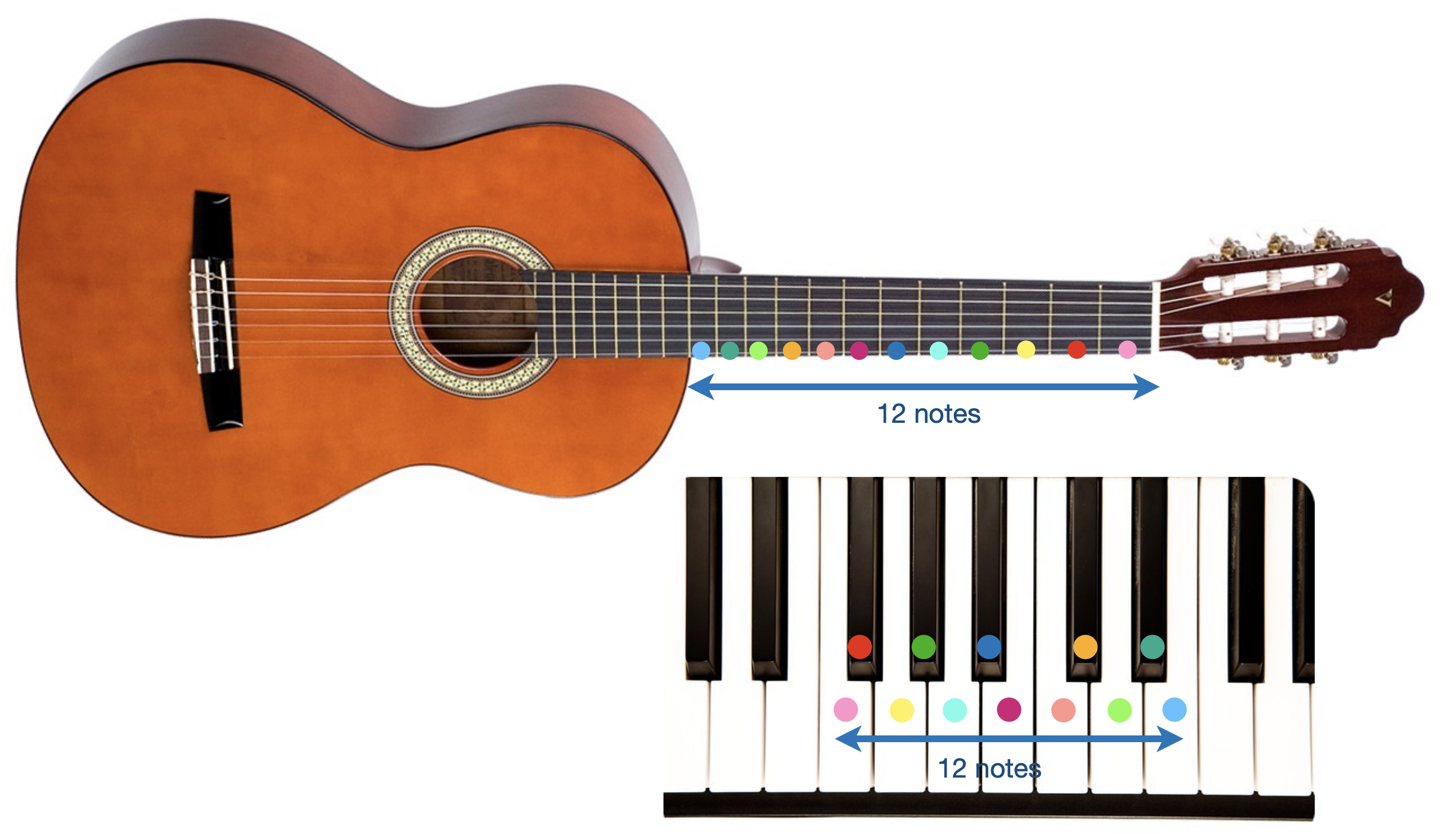
On peut aussi décider de refermer la gamme à la $5^e$ quinte. Cela boucle moins bien mais on obtient alors une gamme qui semble universellement répandue sur Terre : la gamme pentatonique.
En refermant à la $7^e$ quinte, on obtient la gamme diatonique faite de 5 tons et 2 demi-tons à partir desquels on peut obtenir les noms des notes (touches blanches du piano).
Qui “boucle le mieux” entre la gamme pentatonique et la gamme diatonique ?
Enfin, une gamme à 53 niveaux boucle si bien qu’elle sert de base en théorie musicale. Des notes comme Do♯ et Ré♭ n’y’ sont plus confondues.
Les problèmes posés par les gammes de Pythagore
La quinte du loup
Dans la gamme de Pythagore (à 5,7 ou 12 notes), l’une des quintes n’est pas pure (sa valeur a été choisie pour arrêter le cycle alors qu’on ne rebouclait pas exactement sur 1).
Prouver par l’absurde que $\frac{3^n}{2^m}\neq 2$, quels que soient les entiers $n$ et $m$.
Cette quinte, appelée la quinte du loup parce qu’elle rappelle le hurlement du loup, n’est pas consonante avec les autres (elle sonne faux).
L’écart entre la quinte du loup et les autres quintes est appelé comma pythagoricien (représenté en vert ci-dessous). Pour contourner cette difficulté, les compositeurs choisissaient de positionner la quinte du loup dans le cycle sur un intervalle peu utilisé dans leur composition musicale.
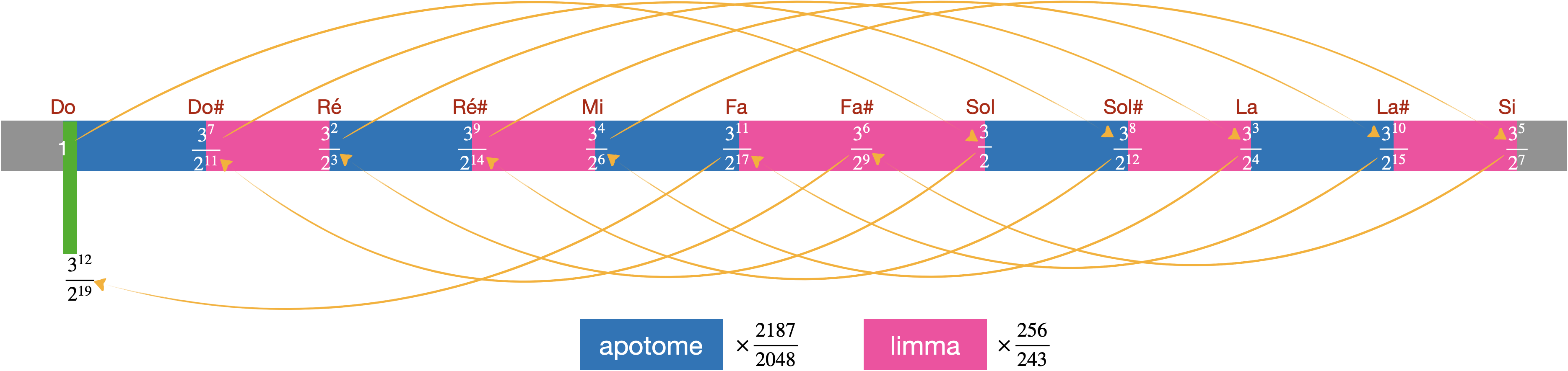
La transposition
La figure précédente fait apparaître deux types d’intervales entre deux notes consécutives. On dit que les gammes de Pythagore sont à tempéraments inégaux.
L’existence de ces deux types d’intervalle pose problème pour la transposition d’un morceau de musique, qui consiste à décaler d’un intervalle fixe toutes les notes de ce morceau afin de l’adapter à la tonalité des instruments ou de la voix.
Rq : l’apotome fait quasiment 5 commas et le limma 4, ce qui donne 53 commas par octave.
Gamme tempérée
L’idée est de moyenner les deux types d’intervalle pour n’avoir plus qu’un seul facteur multiplicatif entre deux notes. On parle alors de gamme au tempérament égal.
Pour y parvenir, on va prendre soin de conserver un facteur 2 parfait entre une note et son octave. On découpe ensuite cette octave en un intervalle unique $x$, appelé demi-ton tempéré, de telle sorte que $x^{12}=2$.
Par tâtonnement et à l’aide d’une calculatrice, trouver un encadrement à $10^{-2}$ près du demi-ton tempéré $x$.
Complétez l’algorithme suivant permettant d’obtenir une valeur approchée à $10^{-k}$ près du demi-ton tempéré $x$ par balayage.
L’opération mathématique permettant d’obtenir $x$ est la racine douzième de 2 : $\sqrt[12]{2}$. On peut aussi écrire $2^{\frac{1}{12}}$ de façon à ce que $x^{12}=(2^{\frac{1}{12}})^{12}=12$.
Expliquer pourquoi le ton tempéré est le carré du demi-ton tempéré. Calculer une valeur décimale approchée à $10^{-2}$ près du ton tempéré.
Sachant que la quinte tempérée est égale à sept demi-tons tempérés, la calculer et la comparer à la quinte pure.
Moralité, dans la gamme tempérée, toutes les quintes sont un peu fausses (mais très peu). C’est le prix à payer pour corriger les deux inconvénients de la gamme pythagoricienne :
- il n’y a plus une quinte plus fausse que les autres ;
- tous les intervalles sont les mêmes $\Rightarrow$ plus de problème de transposition.
Progression arithmétique vs géométrique
Le découpage de l’octave de la gamme tempérée est dit géométrique dans le sens où on avance d’un niveau à l’autre via des multiplications plutôt que par des additions (la progression ne serait alors plus géométrique mais arithmétique ou linéaire).
Résultat : les fréquences correspondant aux notes de la gamme tempérée ne sont pas régulièrement réparties sur une échelle linéaire (où un carreau a toujours la même valeur).
Plus globalement, nos capteurs sensoriels partagent cette sensibilité géométrique aux stimuli extérieurs ; ils ne graduent pas en variations absolues égales mais en variations relatives égales.
On perçoit par exemple la même différence de niveau sonore lorsqu’une trompette est rejointe par une autre trompette, que lorsque 8 trompettes se joignent à 8 autres.
L’échelle utilisée pour le niveau sonore traduit bien cette sensibilité aux variations relatives puisqu’on a dans les deux cas la même augmentation de 3 dB.