Curiosités
La toupie tippe-top
La toupie tippe-top se redresse semblant braver les lois physiques. C’est le couple des forces de frottement qui est responsable de cette bizarrerie.
Wolfgang Pauli et Niels Bohr, deux immenses physiciens au cœur de la révolution quantique, regardant une toupie tippe-top se relever.

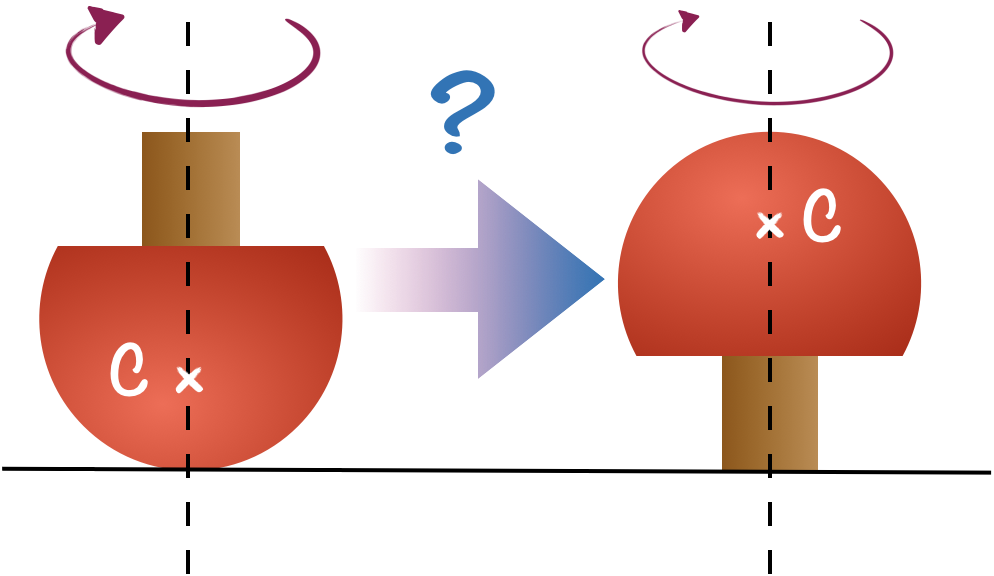
Comme le centre de masse s’est élevé, on a envie de s’inquiéter pour la conservation de l’énergie Mais il ne faut pas ! Elle est solide… La toupie tourne moins vite à la fin qu’au début. Une partie de l’énergie de rotation est partie dans les frottements et une autre dans le retournement.
D’où vient la force qui amène la toupie à se retourner ? Pauli et Bohr se sont sans doute posés la question moins d’un quart de seconde
mais chacun son rythme…
Comme c’est une toupie, on pense rapidement à un mouvement de précession. La précession est un mouvement de rotation lent (par rapport à la rotation propre) du centre de masse du solide. Or elle naît quand un couple est appliqué sur le solide et cette rotation se fait autour de la direction de la force provoquant le couple.
Formidable vidéo de VSauce expliquant les gyroscopes :
Première candidat pour l’origine du couple redressant la toupie : le poids. Bof… Le moment du poids n’a pas la bonne direction puisqu’il entraîne la toupie dans un mouvement de rotation autour d’un axe vertical et non horizontal (et contrairement à une toupie classique, le centre de masse est très bas et donc le bras de levier très court, ce qui donne un couple de faible intensité).
Il nous faudrait une précession autour d’un axe horizontal pour faire pivoter la toupie et pour ça, on a besoin d’un moment d’axe vertical et donc finalement une force elle-même horizontale !
Son origine devient claire si l’on s’attarde sur la grande différence entre cette toupie et les toupies classiques (outre la position du centre de masse) : elle n’a pas de pointe ! Le point de contact peut se balader le long de la partie arrondie de la toupie, ce qui le désaligne avec l’axe de rotation principal.
Dès que la toupie bascule un peu, le point de contact $I$ s’éloigne du sommet $H$ et la toupie se met à précesser (sous l’action du poids) autour d’un axe vertical. Cette précession entraîne le point de contact $I$ dans un mouvement circulaire (en première approximation) et comme la toupie tourne trop vite autour de son axe de symétrie pour pouvoir rouler, elle glisse. Donc le point de contact glisse sur la surface et subit des forces de frottement de glissement $\vec{f}$. On a trouvé notre force horizontale ! Le moment de la force de frottement crée la précession qui va pivoter notre toupie.
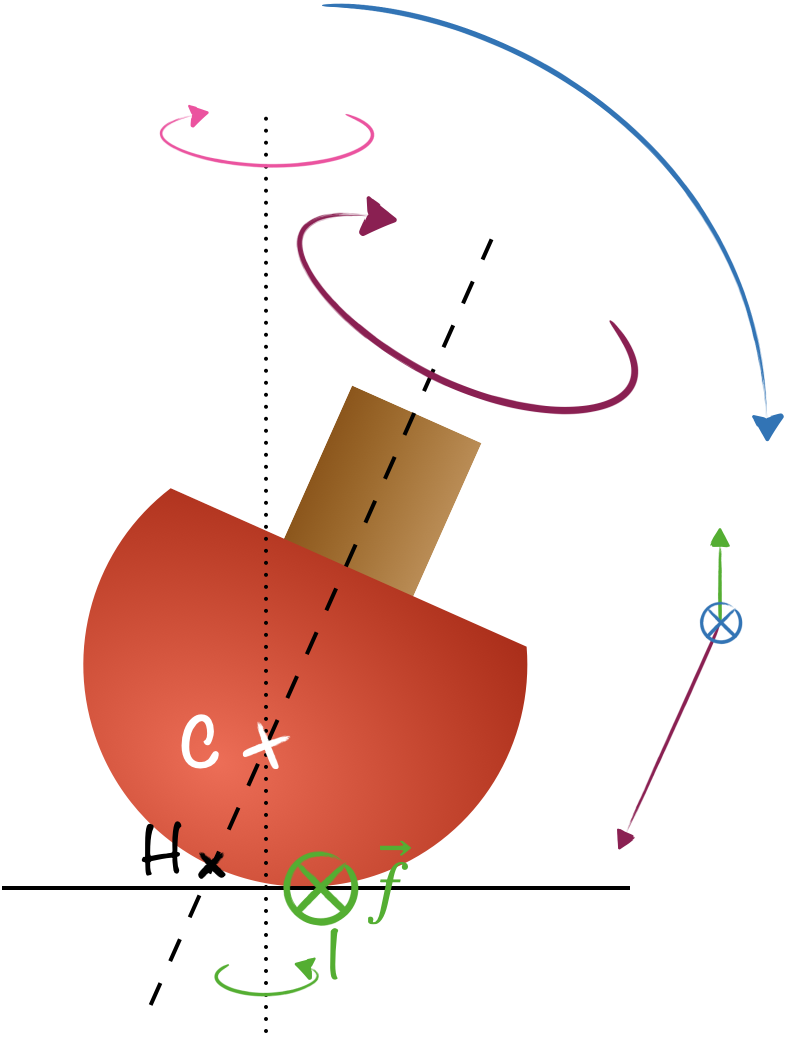
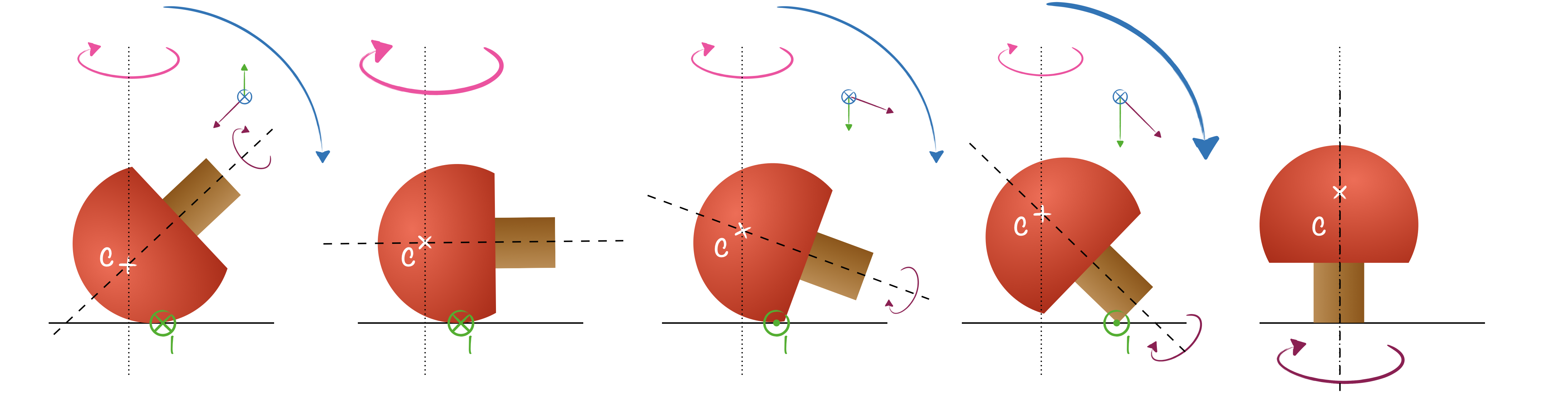
Plus la toupie penche, plus la rotation autour de l’axe vertical s’accélère tandis que celle autour de l’axe de symétrie ralentit. C’est la conservation du moment cinétique qui l’impose. Le couple de redressement devient, lui, de plus en plus faible au fur et à mesure de la diminution de la rotation propre de la toupie.
Lorsque la toupie est horizontale, la rotation de la toupie autour de son axe de symétrie s’arrête et donc le couple de redressement disparaît momentanément. Mais entraînée par son élan, la toupie ne reste pas horizontale longtemps…
Une fois la position horizontale dépassée, la rotation propre de la toupie redémarre, mais elle est inversée par rapport à celle de départ (c’est toujours la conservation du moment cinétique qui se manifeste). Et l’échange entre les deux rotations (celle autour de l’axe vertical et celle autour de l’axe de symétrie de la toupie) continue, mais au bénéfice maintenant de la rotation propre qui se fait de plus en plus rapide au fur et à mesure du basculement. Le moment lié aux forces de frottement reprend lui aussi du poil de la bête et va se renforcer avec la vitesse de rotation propre. Et surtout, il est dans le même sens que précédemment puisque l’inversion de la rotation propre de la toupie est compensée par l’inversion du sens des forces de frottement ! Il continue donc de redresser la toupie.
Vient ensuite le contact entre le pied et le sol. Le bras de levier du moment des forces de frottement augmente d’un coup donnant un petit “kick” à la remontée. Il faut néanmoins une réserve d’énergie suffisante, les frottements ayant dispersé dans le support une partie non négligeable de l’énergie initiale et l’élévation du centre de masse ayant lui-aussi aussi puisé dans la réserve cinétique.
Une fois redressée, les frottements (sur les bords du pied) continuent à stabiliser la position de la toupie, le centre de masse etant ramené en position verticale.
L’anagyre
L’anagyre (ou rattleback en anglais) refuse obstinément de tourner dans le sens qu’il n’aime pas. Si par malheur on l’y envoie, il freine, rouspète dans un bruit de crécelle (rattle en anglais) puis se met à tourner dans le bon sens, le seul, le vrai.
En effet, son Créateur lui a choisi un sens en le rendant asymétrique.
Supposons qu’un anagyre ait été fabriqué à partir d’un demi-ellipsoïde auquel on a ajouté de la masse en deux endroits symétriques par rapport à son centre. Son axe principal d’inertie est alors décalé par rapport à ses axes de symétrie géométrique (cf. dessin ci-dessous).
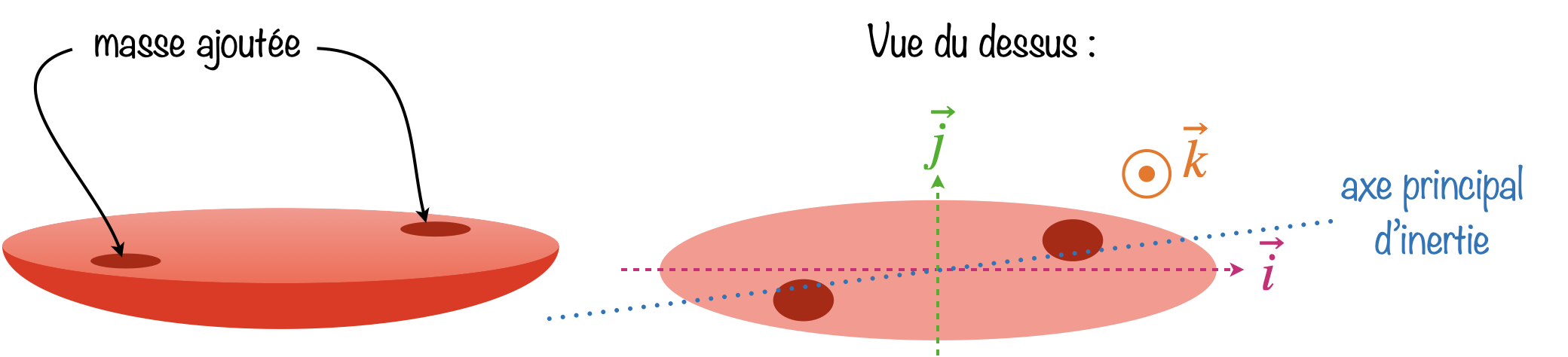
La conséquence du décalage de l’axe d’inertie est le couplage entre les différentes rotations de l’anagyre. C’est très visible lorsqu’on le fait osciller d’avant en arrière (autour de $\vec{j}$) puisqu’apparaît immédiatement une oscillation de gauche à droite (autour de $\vec{i}$) et une rotation dans le sens des aiguilles d’une montre (autour de $\vec{k}$).
Imaginons dans un premier temps que les deux masses soient sur l’axe de symétrie ($\vec{i}$) et regardons leur mouvement si l’anagyre oscille dans le sens de la longueur (autour de l’axe $\vec{j}$).
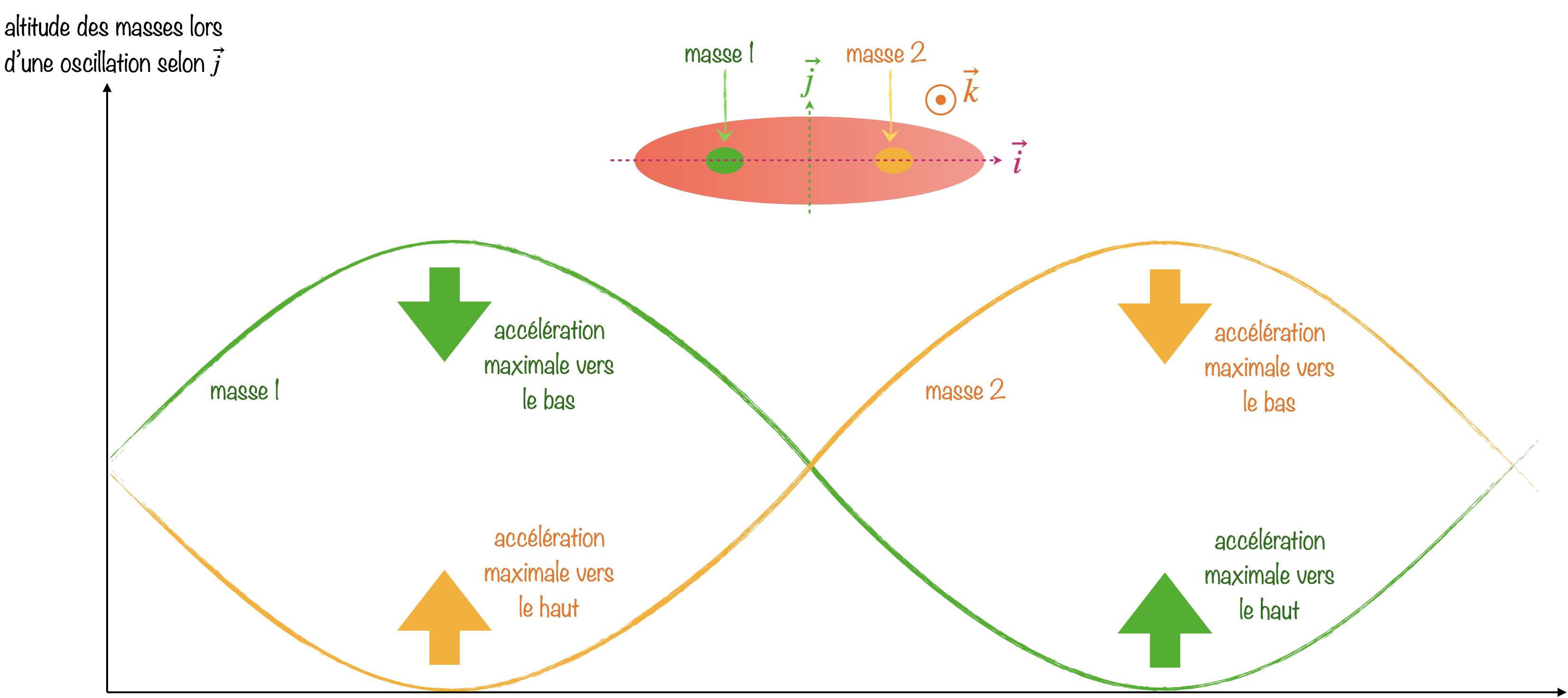
La 2e loi de Newton appliquée à la masse $i$ nous dit que $\vec{F}_{\text{anagyre sur masse i}} = m_{\text{masse i}}\left(\vec{a}_{\text{masse i}}-\vec{g}\right)$. Quand $\vec{a}$ et $\vec{g}$ sont dans le même sens, la force de l’anagyre sur la masse est moins grande. Donc $F$ est plus grande lorsque la masse est au plus bas. De plus, la 3e loi de Newton nous dit que $\vec{F}_{\text{masse i sur anagyre}} = -\vec{F}_{\text{anagyre sur masse i}} $. On se retrouve donc avec la situation schématisée ci-dessous :
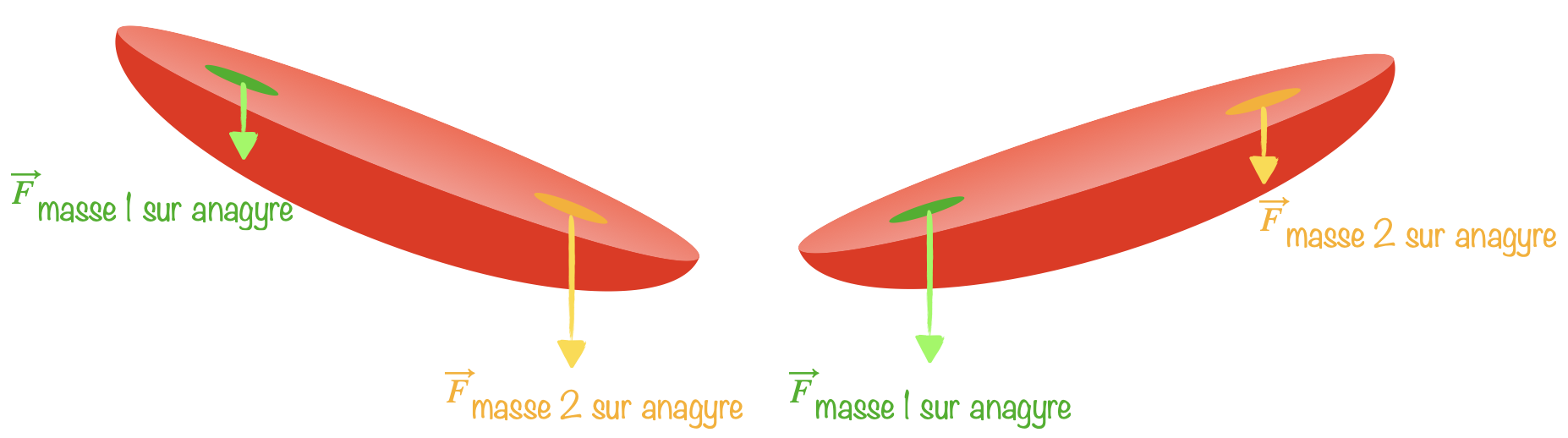
Maintenant si on redécale les deux masses par rapport à l’axe de symétrie dans la direction de $\vec{j}$, on comprend mieux comment la rotation selon $\vec{j}$ se couple avec celle selon $\vec{i}$. La masse la plus basse exerce sur l’anagyre une force plus grande que la plus haute, ce qui provoque un moment auour de $\vec{i}$.
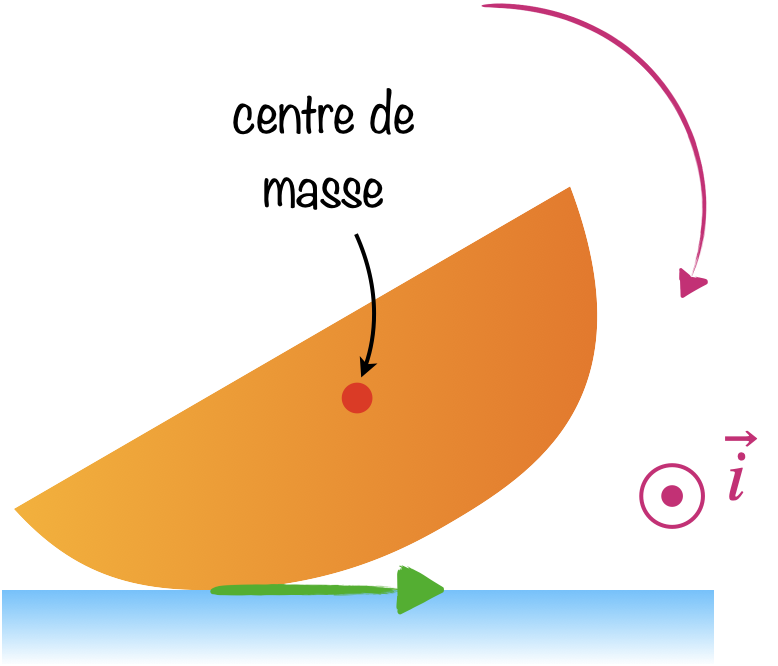
Finalement, lorsque l’anagyre oscille d’avant en arrière, la partie surélevée va chuter “en se tournant” du côté de sa masse ajoutée. Imaginons que c’est la partie avant qui redescend en entraînant une rotation autour de $\vec{i}$ dans le sens négatif (cf. vidéo ci-dessous).
Au point de contact, l’anagyre exerce alors sur le sol une force selon $-\vec{j}$ et réciproquement, le sol exerce une force selon $+\vec{j}$ sur l’anagyre. Lorsque c’est la partie arrière qui redescend, la rotation selon $\vec{i}$ se fait dans le sens positif, ce qui donne au final une force du sol selon $-\vec{j}$. Le sol exerce donc un couple sur l’anagyre le faisant tourner autour de $\vec{k}$ dans le sens positif (anti-horaire).
Lorsqu’on envoie l’anagyre dans le sens impie (horaire ici), la moindre petite oscillation selon $\vec{i}$ ou $\vec{j}$ va être amplifiée car elle entraîne, comme on l’a vu, un mouvement de rotation dans l’autre sens qui va freiner l’anagyre et le cambrer à la manière d’un freinage sur la roue avant d’un vélo augmentant ainsi l’amplitude des oscillations. L’augmentation de l’amplitude augmente à son tour la force du sol sur l’anagyre qui augmente le cambrage… C’est une rétroaction positive. La rotation autour de $\vec{k}$ finit par être stoppée et les importantes oscillations autour de $\vec{i}$ et $\vec{j}$ relancent ensuite la rotation autour de $\vec{k}$ dans l’autre sens.
Un deuxième type d’anagyre est plus simple à comprendre car sa forme elle-même est asymétrique. En effet, la ligne de crête de sa partie basse dessine un S.

Lors d’une oscillation d’avant en arrière, l’anagyre va reposer préférentiellement sur sa partie la plus plate ce qui le fait basculer autour de $\vec{i}$. Le sol s’oppose à ce mouvement faisant tourner l’anagyre autour de $\vec{k}$.
L’oiseau buveur
L’oiseau buveur estt une star (on le retrouve dans Alien ou les Simpsons par exemple).

Et c’est aussi un bon exercice de thermodynamique (qui a été donné au concours de Centrale il y a un bail).
Explication par Sixty Symbols en utilisant une caméra thermique :