Chaos
Au confin des maths et de la physique, une des plus belle chose qui soit : le chaos (avec son cheptel de fractales et d’attracteurs étranges). Le chaos n’a pas grand chose à voir avec son image “grand public” puisqu’il est finalement très organisé. Mais timide, il le cache bien…
L’intégration du système d’équations différentielles suivant donne le fameux attracteur de Lorenz avec sa forme caractéristique de papillon :
$$\begin{cases}x’=\sigma(y-x)\\y’=\rho x-y-xz\\z’=xy-\beta \end{cases}$$
Avec les valeurs de paramètres suivantes :
$$\begin{cases}\sigma = 3\\\rho = 26.5\\\beta = 1\end{cases}$$
et le point de départ $(x_0;y_0;z_0)=(0;1;1,05)$, cela donne :
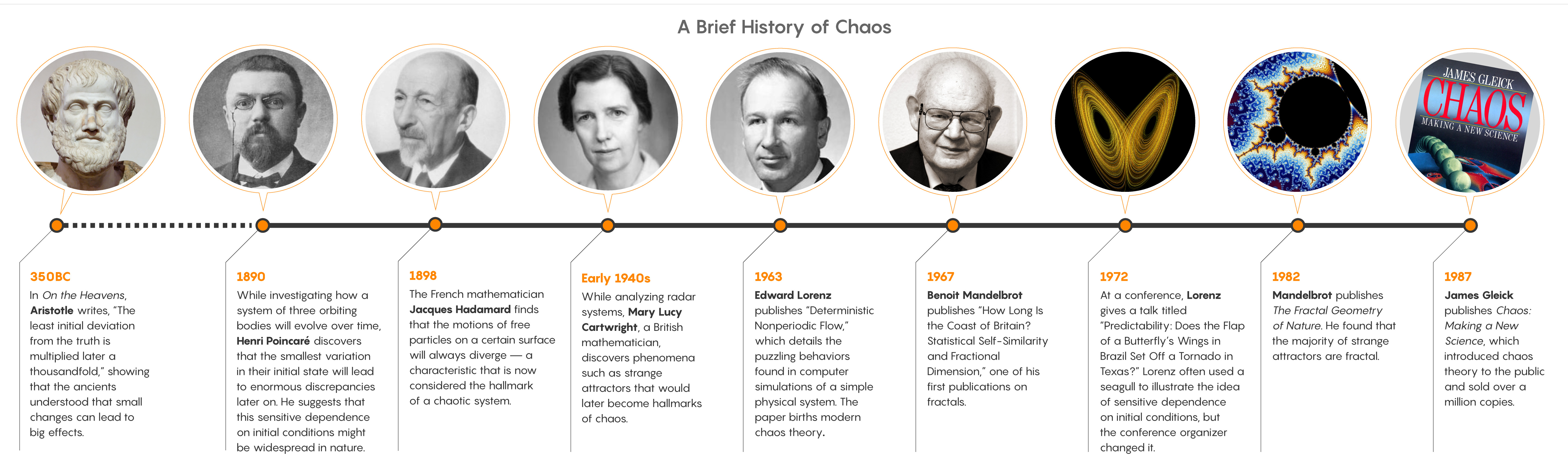
Cet article relate l’histore du chaos en tant qu’objet de recherche et insiste en particulier sur le rôle fondamental de deux programmeuses : Ellen Fetter et Margaret Hamilton.
Le livre Nonlinear Dynamics and Chaos de Steven Strogatz introduit le domaine de manière passionnante.