Poursuites
Cette page est très inspirée du livre Chases and Escapes The Mathematics of Pursuit and Evasion de Paul Nahin.
Paradoxe d’Achille et de la tortue
Dans La Physique, Aristote rapporte les célèbres paradoxes de Zénon d’Élée dont celui d’Achille et la tortue. :
Celui qui court le plus lentement ne sera jamais rattrapé par le plus rapide. Car le poursuivant doit d’abord atteindre le point d’où est parti le poursuivi, si bien que le plus lent doit toujours avoir une longueur d’avance.
Imaginons qu’Achille aille deux fois plus vite que la tortue et que la tortue ait une distance d’avance $d$ au départ. Il faut un temps $T$ à Achille pour parcourir la distance $d$, mais pendant ce temps $T$, la tortue a continué d’avancer et a parcouru une distance $d/2$. Il faudra alors $T/2$ à Achille pour parcourir cette distance supplémentaire, mais pendant ce temps, la tortue a avancé de $d/4$, etc.
Le temps mis par Achille pour rattraper la tortue vaut donc :
$\displaystyle T+\frac{T}{2}+\frac{T}{4}+\frac{T}{8}+\cdots = \sum_{n=0}^{\infty}\frac{T}{2^n}$
Le but de Zénon d’Élée était de prouver l’impossibilité même du mouvement en piégeant le concept avec ces histoires d’infini.
Réussir à imaginer que la somme d’un nombre infini de termes positifs puisse donner un résultat fini constitua une montagne mathématique qu’on mis très longtemps à gravir.
Ajourd’hui, on sait que ce type de série géométrique converge si sa raison est comprise dans $]-1;1[$. Et dans notre exemple, comme l’illustre l’animation ci-dessous, la série converge pour donner $2T$.

Courbe de poursuite
Ok, on peut rattraper la tortue, mais comment faire en pratique si on devait programmer Achille en supposant que les deux démarrent dans les poitions notées ci-dessous ?
- Le plus rapidement : calculer la direction de la ligne droite à suivre permettant d’intercepter la tortue.
- Le plus simple : toujours orienter son vecteur vitesse (la direction de son mouvement) vers la cible.
Dans le deuxième cas, on obtient une famille de courbes particulières appelées courbes de poursuite.
Extrait d’un manuel de l’US Air Force distribué aux mitrailleurs :

Comme l’explique le manuel, si un poursuivant se dirige en permanence vers sa cible (son vecteur vitesse étant selon la ligne joignant le poursuivant à la cible) alors sa trajectoire sera une courbe de poursuite.
Si on voulait déterminer analytiquement l’équation de cette courbe, on poserait que :
- la pente $p(x)$ de la trajectoire du chasseur est donnée par $\displaystyle p(x)=\frac{dy}{dx}=\frac{y-V_{cible}t}{x-x_0}$ d’après le schéma ci-dessous.
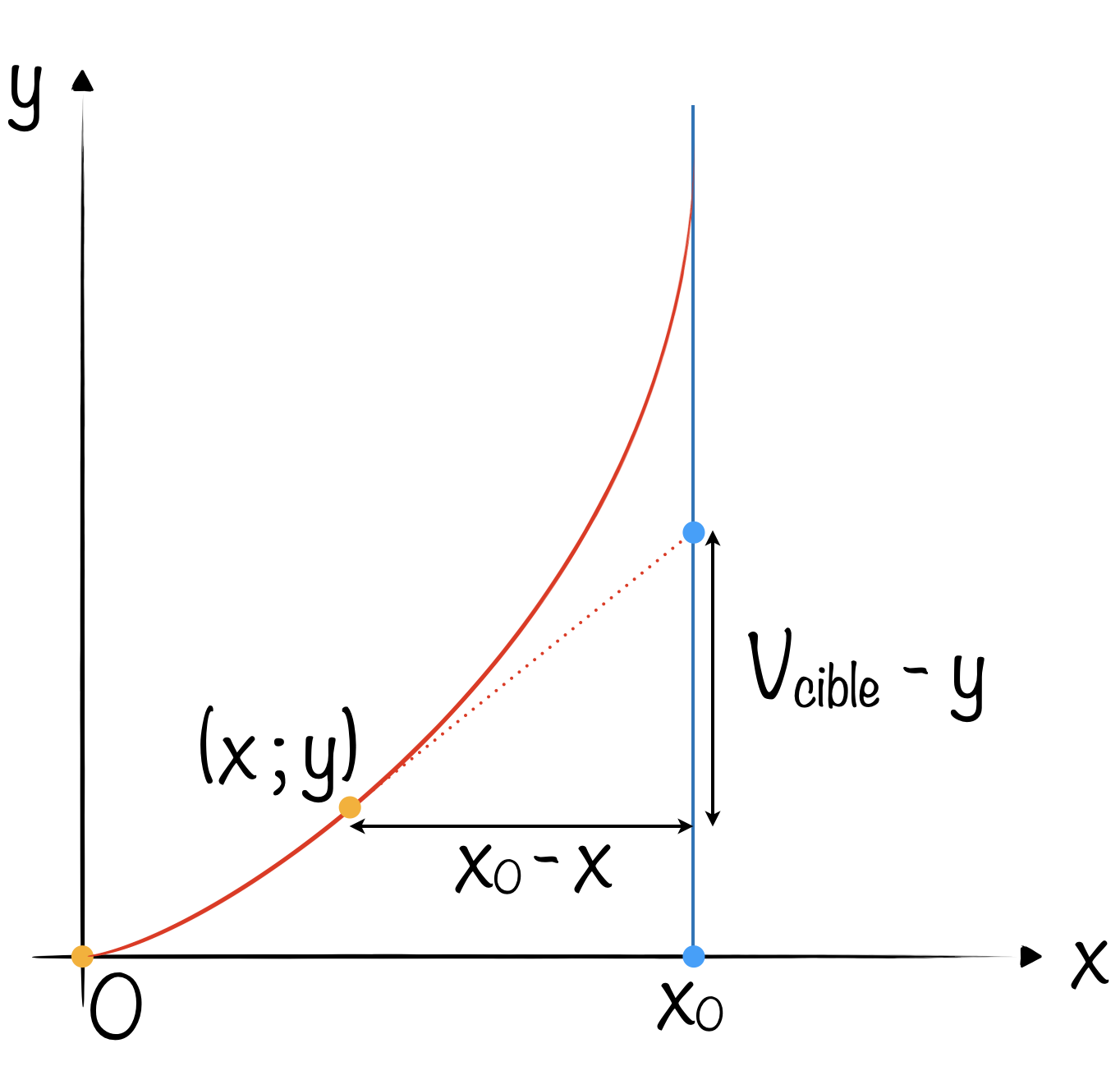
- et le chasseur parcours en un temps $t$ le morceau de trajectoire compris enntre $0$ et $x$ : $\displaystyle V_{chasseur} t = \int_0^x \sqrt{1+\left(\frac{dy}{dx’}\right)^2}dx’ = \int_0^x \sqrt{1+p(x’)^2}dx’ $
En résolvant pour $t$, on obtient $\displaystyle \frac{1}{V_{chasseur}}\int_0^x\sqrt{1+p(x’)^2}dx’ = \frac{y}{V_{cible}}-p(x)\frac{(x-x_0)}{V_{cible}}$
Après quelques étapes, cela s’intègre en $\displaystyle p(x)=\frac{dy}{dx}=\frac{1}{2}\left[\left(1-\frac{x}{x_0}\right)^{-n}-\left(1-\frac{x}{x_0}\right)^{n}\right]$ en posant $\displaystyle n = \frac{V_{cible}}{V_{chasseur}}$ qui s’intègre à son tour en $\displaystyle y(x)=\frac{n}{1-n^2}x_0 + \frac{1}{2}(x_0-x)\times\left[\frac{(1-x/x_0)^n}{1+n}-\frac{(1-x/x_0)^{-n}}{1-n}\right]$.
La cible est rattrapée au point $(x_0\,;y(x_0))=\left(x_0\,;\frac{n}{(1-n^2)}x_0\right)$. Elle a alors parcouru une distance $\displaystyle \frac{n}{(1-n^2)}x_0$ et le chasseur a parcouru $\displaystyle \frac{V_{chasseur}}{V_{cible}}$ fois plus.
C’est finalement beaucoup plus simple à programmer qu’à calculer. Et si la cible se met à remuer, cela devient même mission quasi impossible d’obtenir une formule fermée pour la courbe…
Dans ce premier petit programme, on retrouve la courbe d’allure caractéristique.
Et dans ce deuxième programme, on prend le point de vue du passager de l'avion cible pour confirmer la mise-en-garde du manuel ; si le chasseur semble glisser dans le ciel tout en grossissant, ça n'est pas bon signe...
Interception
Arrêtons maintenant de poursuivre bêtement et essayons d’intercepter.
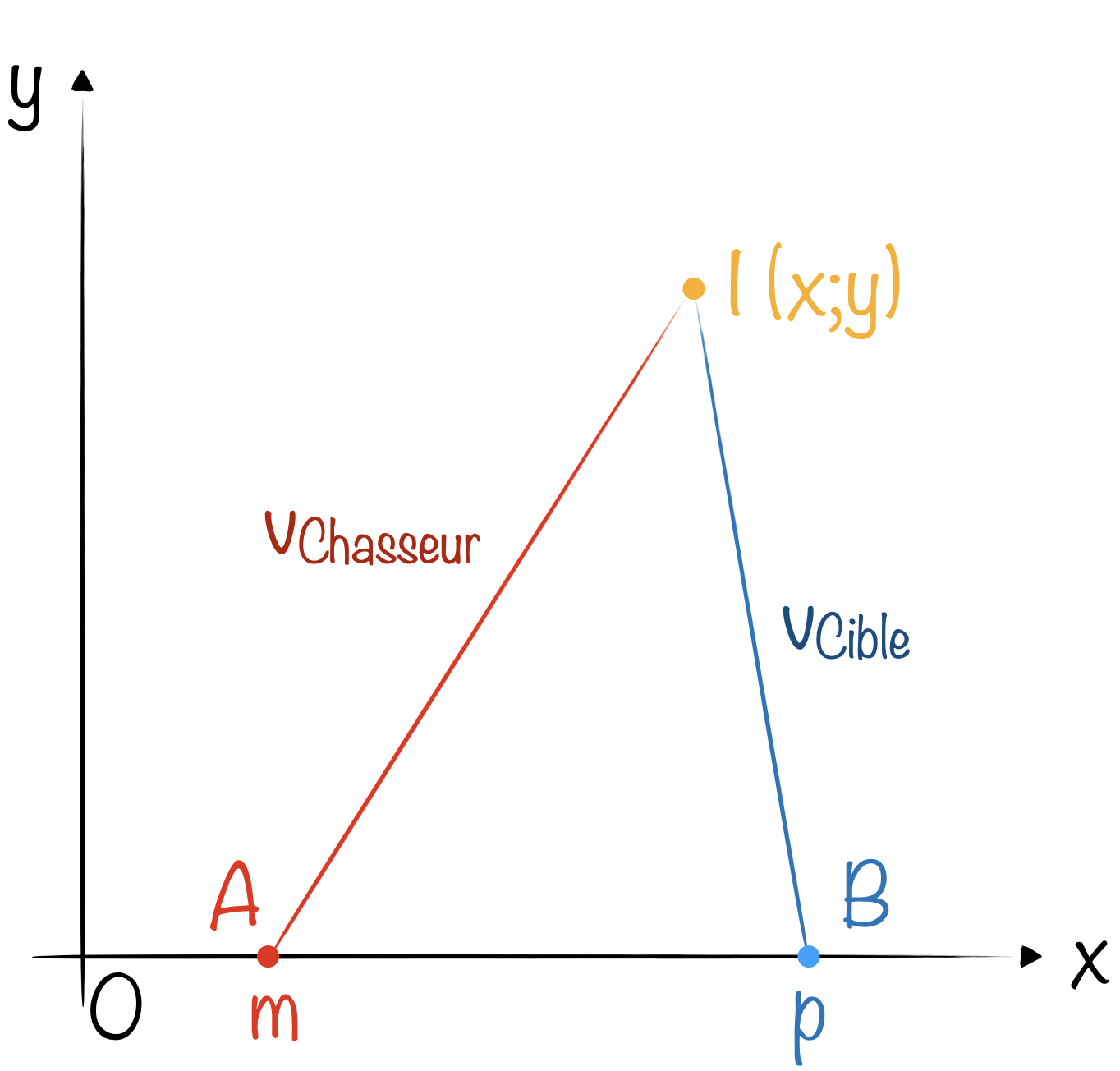
Supposons que le chasseur est en $A$ à $t=0$ et que la cible est en $B$ au même instant et supposons aussi qu’ils ont chacun un mouvement rectiligne uniforme (à $v_{chasseur}$ et $v_{cible}$). À quelle condition le chasseur intercepte-t-il la cible au point $I$ ?
Il faut que le ratio des distances et des vitesses soient les mêmes : $\displaystyle \frac{BI}{AI}=\frac{v_{cible}}{v_{chasseur}}=n$.
Les points $I$ solutions doivent donc vérifier : $\displaystyle \frac{\sqrt{(x-p)^2+y^2}}{\sqrt{(x-m)^2+y^2}}=n$.
Cela donne l’équation d’un cercle, le cercle d’Apollonius : $\displaystyle \left[x-\frac{n^2 m-p}{n^2-1}\right]^2 + y^2 = \left[\frac{n(p-m)}{1-n^2}\right]^2$.
Son centre est sur l’axe horizontal $\displaystyle \left(\frac{n^2m-p}{n^2-1};0\right)$ et son rayon vaut $\displaystyle \frac{n(p-m)}{|1-n^2|}$.
Pour déterminer la direction à prendre pour le chasseur, il suffit de regarder où la direction de la cible coupe le cercle d’Apollonius.
On remarque que même si la cible va plus vite que le chasseur $n>1$, il peut y avoir interseption (et pour deux directions différentes du chasseur). Mais pour cela, l’angle $\theta$ de la direction de la cible ne doit pas être supérieur à $\displaystyle \sin^{-1}\left(\frac{v_{chasseur}}{v_{cible}}\right)$.
En effet, la situation limite correspond à une direction de la cible tangente au cercle d’Apollonius (voir dessin ci-dessous).
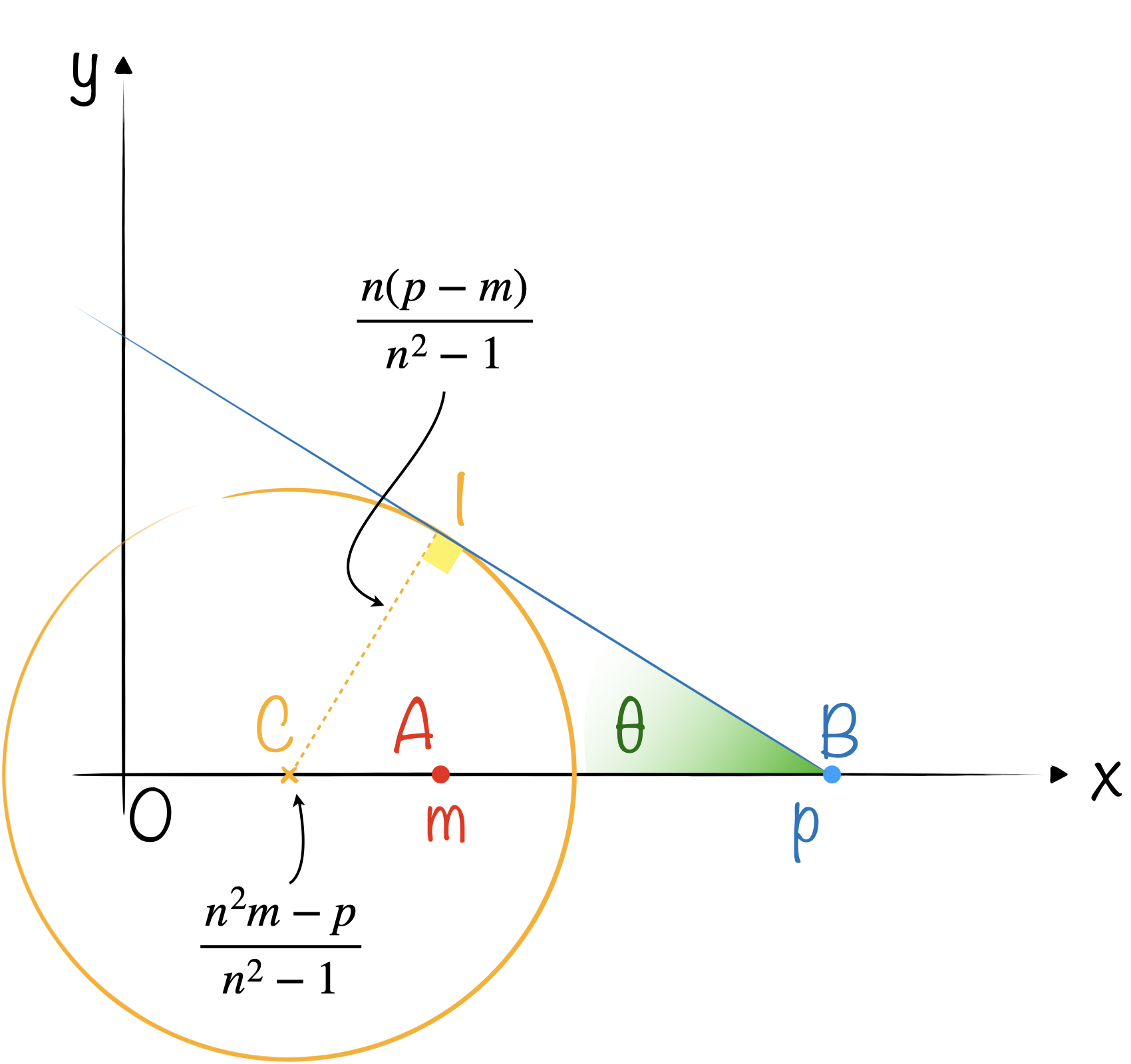
On a bien $\displaystyle \sin\theta = \frac{CI}{CB} = \frac{\frac{n(p-m)}{n^2-1}}{p-\frac{n^2m-p}{n^2-1}}=\frac{1}{n}$
Manœuvre d’évitement de l’Enola Gay
Juste après avoir lâcher sa terrible bombe sur Hiroshima, l’Enola Gay a manœuvré pour tenter d’éviter au maximum le souffle de l’explosion atomique.
Le B-29 avait une vitesse de $\pu{529 km/h}$ par rapport au sol au moment du largage de la bombe. Sachant que l’explosion a eu lieu après une chute de $\pu{19700 ft}$, soit $\pu{9,053 km}$, on peut en déduire le délai entre le largage et l’explosion : dans l’hypothèse d’une chute libre (poids comme seule force), la distance verticale parcourue est donnée par $h=\frac{1}{2}gt^2$, d’où $t=\sqrt{\frac{2h}{g}}\approx\pu{43 s}$. C’est en accord avec la valeur généralement admise. Le pilote a donc environ 43 secondes pour s’éloigner le plus possible de la zone d’impact.
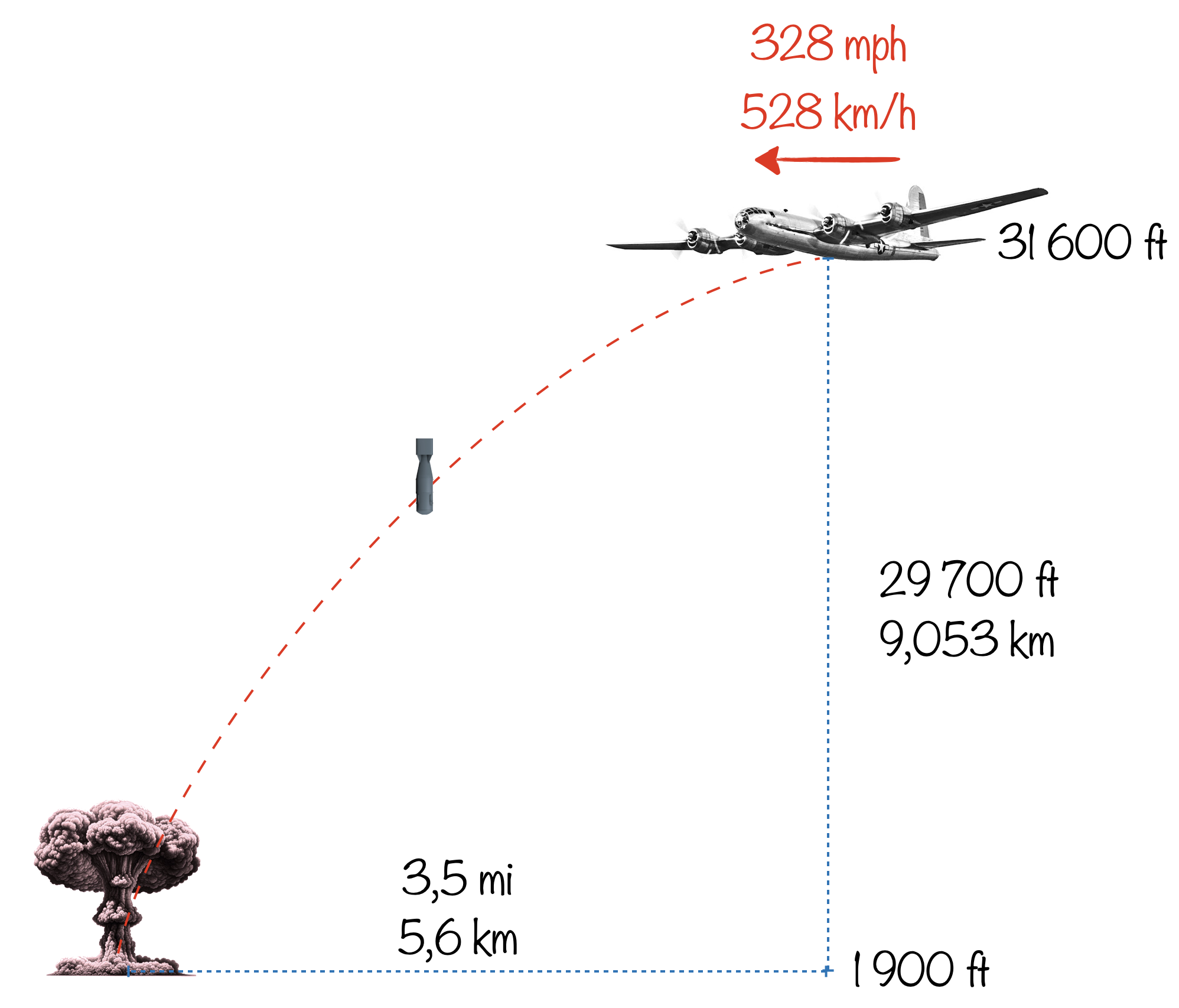
Pendant ces 43 secondes, la bombe continue d’avancer horizontalement à la vitesse de l’avion au moment du largage, ce qui donne une distance parcourue de $\pu{6,3 km}$. Le pilote parle plutôt d’une distance horizontale de 3,5 mi, soit $\pu{5,6 km}$. Vu la forme de la bombe, cela paraît logique que son mouvement horizontal soit plus impacté par les frottements que son mouvement vertical.
Au moment du largage, le pilote va évidemment chercher à séloigner le plus possible de la future explosion. Pour cela il entreprend immédiatement un virage à pleine vitesse (350 mph par rapport à l’air, soit $\pu{563 km/h}$) en braquant ses ailes à un angle $\alpha = 60^\circ$.
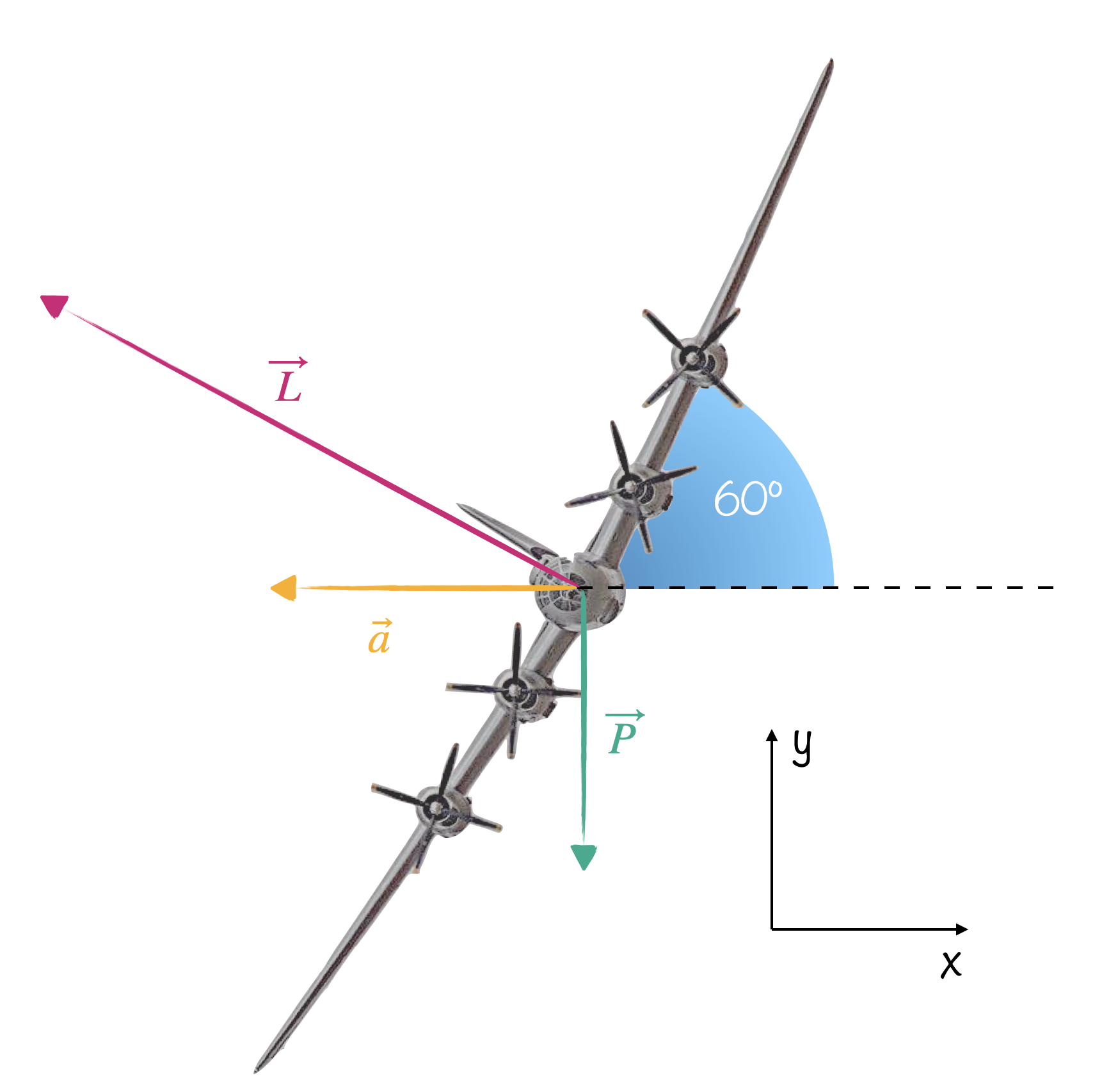
Si le B-29 tourne, c’est grâce à l’inclinaison de la force de portance $\vec{L}$, perpendiculaire aux ailles. On va supposer que la trajectoire pendant le virage est circulaire de rayon $R$ et que la vitesse $v$ de l’avion par rapport à l’air reste constante. L’accélération est alors horizontale et purement centripète et vaut $\displaystyle a = \frac{v^2}{R}$.
Le PFD (2e loi de Newton) appliqué à l’avion nous dit que : $\displaystyle\vec{P}+\vec{L} = m\vec{a}$.
En projetant verticalement, on obtient : $\displaystyle-mg+L_y = 0$. On retrouve que la composante verticale de la portance compense le poids. Cela donne : $\displaystyle L\times\cos\alpha = mg$.
Et la projection horizontale donne : $\displaystyle -L_x = -ma$, et donc $\displaystyle L\sin\alpha = ma$.
Par conséquent : $\displaystyle ma=\frac{mg}{\cos\alpha}\sin\alpha \Rightarrow a = g\tan\alpha$.
Comme $\displaystyle\tan(60^\circ) = \sqrt{3}$, on se retrouve avec une accélération horizontale de l’avion valant $\sqrt{3}g$.
Les passagers de l’avion ressentent, eux, une accélération oblique de $2g$ (accélération du champ de pesanteur à laquelle s’ajoute l’accélération perpendiculaire due à l’avion).
Et puisque $\displaystyle a=\frac{v^2}{R}$, on obtient : $\displaystyle R =\frac{v^2}{g \tan\alpha} \approx \pu{1,4 km}$. Un petit coucou ou un gros porteur feront le même virage du moment que vitesse et inclinaison des ailes sont les mêmes !
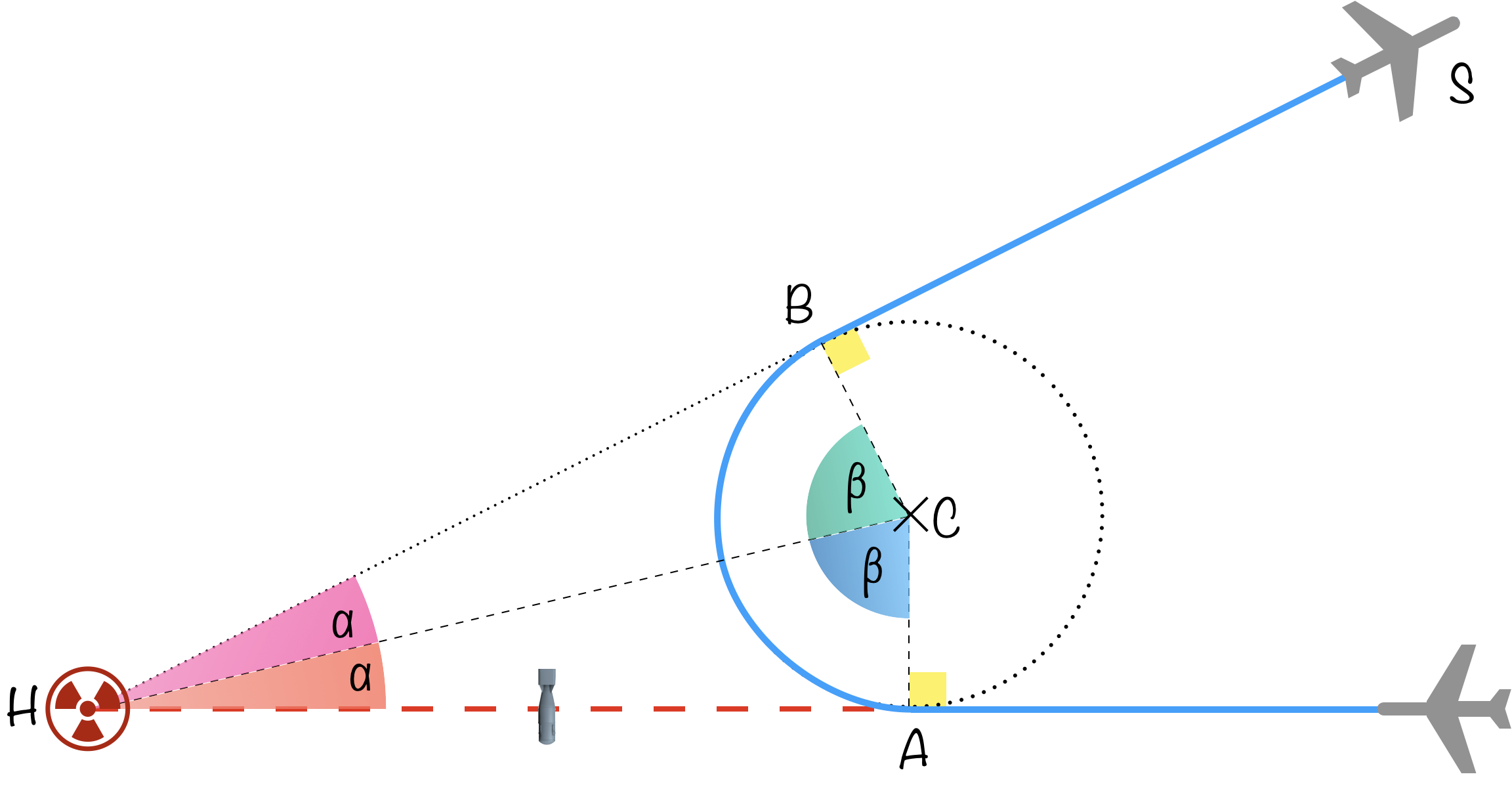
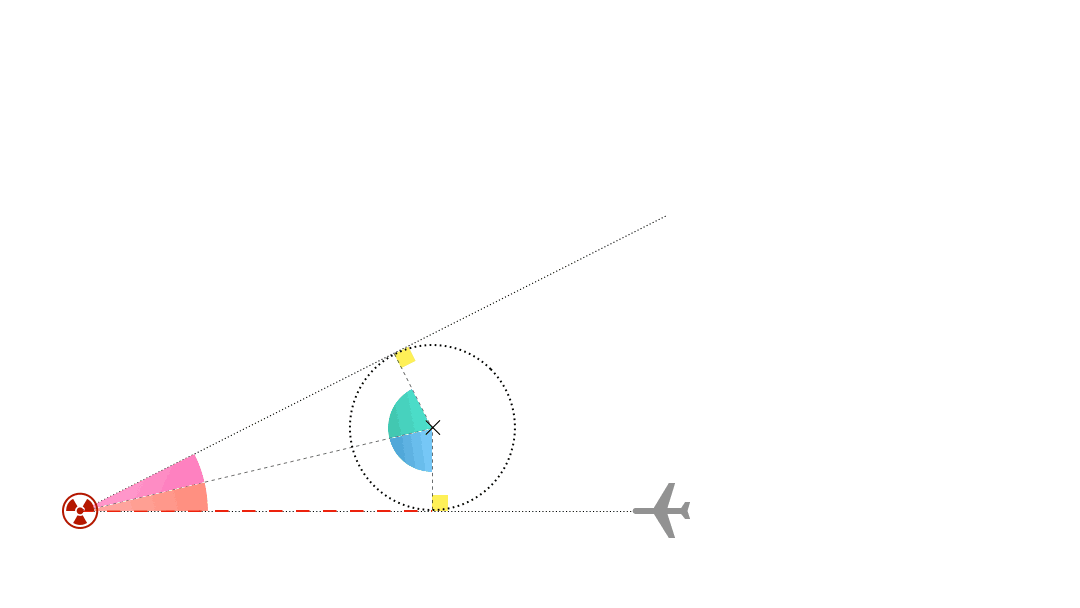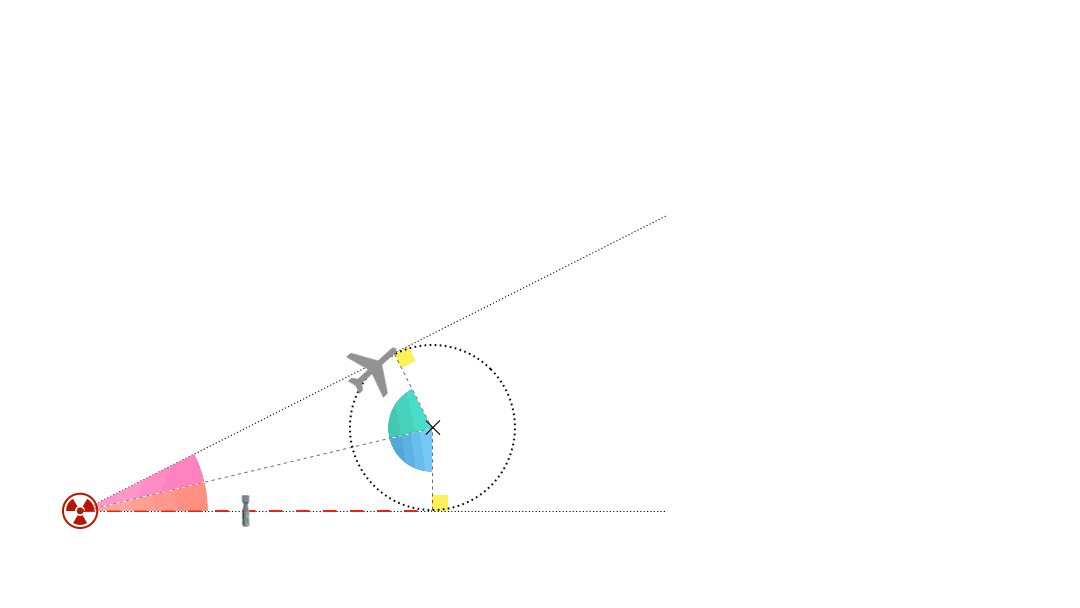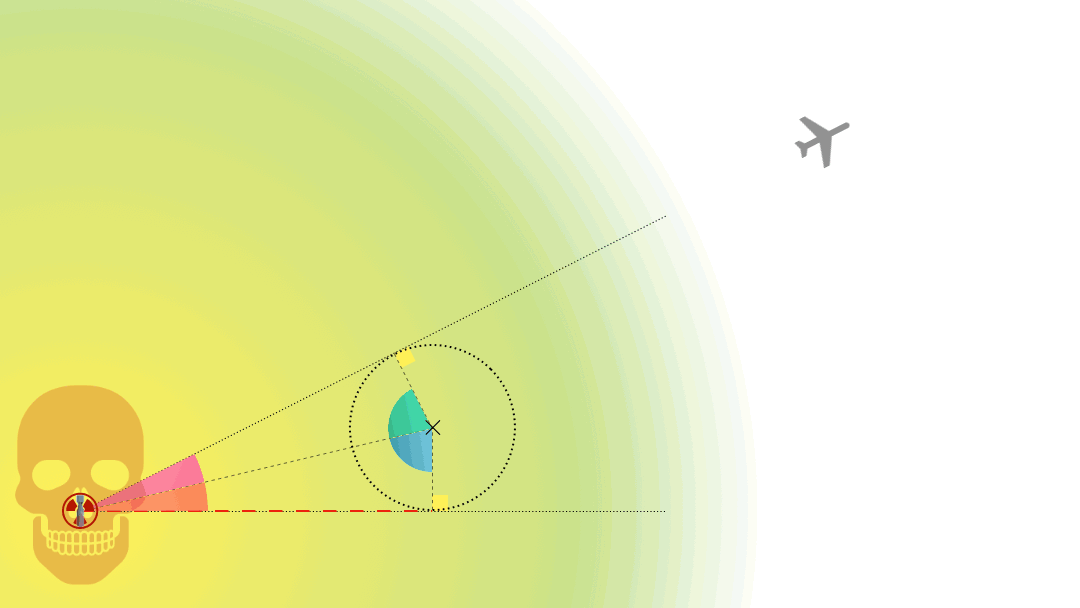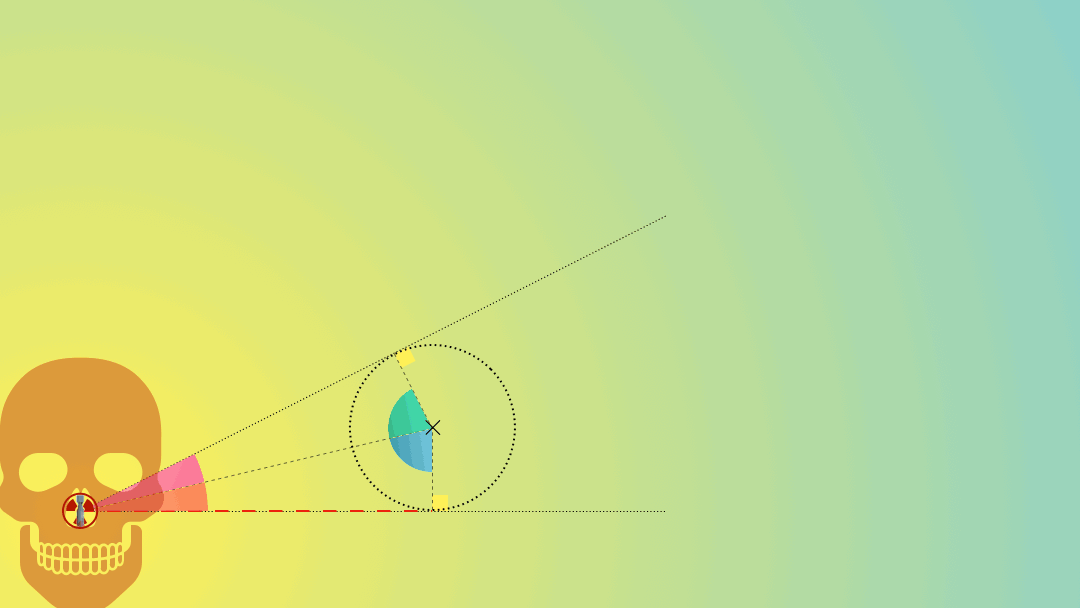
Il nous reste à trouver quand quitter le virage. $(AH)$ et $(HB)$ sont tangentes au cercle formé et $AH=AB$. Les triangles $HBC$ et $HAC$ sont donc identiques impliquant l’égalité des angles $\widehat{HCB}$ et $\widehat{HCA}$ ($\beta$ sur le schéma). Le bombardier quitte le virage au bout d’une déviation de $2\beta$ où $\beta = \arctan\left(\frac{AH}{R}\right)=\arctan(5,6/1,4)$. Cela donne une déviation totale $2\beta$ d’environ $152^\circ$.
La distance parcourue sur le cercle vaut alors $\frac{2\beta}{360}\times 2\pi R \approx \pu{3,7 km}$ et le temps pour la parcourir vaut $3,7/545\times 3600 = \pu{24 s}$. Pour la vitesse de l’avion, on fait une moyenne entre la vitesse de l’avion par rapport au sol au moment du largage et sa vitesse par rapport à l’air. Il reste alors $43-24=\pu{19 s}$ pour s’éloigner à tout berzingue avant que la bombe n’explose. Le bombardier sera alors à une distance $d=5,6+545\times 19/3600 \approx \pu{8,5 km}$.
Au bout de combien de temps sera-t-il touché par le souffle de l’explosion, et à quelle distance de l’impact sera-t-il alors ? Supposons une onde de choc se déplaçant à $v_c$ d’environ $\pu{1300 km/h}$ (un peu plus rapide que le son) et appelons $t_i$ le temps au bout duquel le souffle rattrape le bombardier (de vitesse $v_b = \pu{545 km/h}$). N’oublions pas que le bombardier est à la hauteur $h$ par rapport au point d’impact ($\approx\pu{9,1 km}$) au-dessus du point d’impact. Pythagore donne alors : $(v_c\times t_i)^2 = (d+v_b\times t_i)^2+h^2$. La solution positive de ce trinôme du second degré en $t_i$ est $\pu{0,0144 h}$ soit $\pu{52 s}$ environ. Le pilote parle plutôt d’un délai de $\pu{45 s}$ après la détonation et d’une distance de $\pu{11,5 mi}$ au point d’impact. Si notre résultat surestime le délai, il donne une distance à l’impact de $0,0144\times 1300 \approx \pu{18,7 km} = \pu{11,6 mi}$. L’accord n’est pas mauvais.
Poursuite cyclique
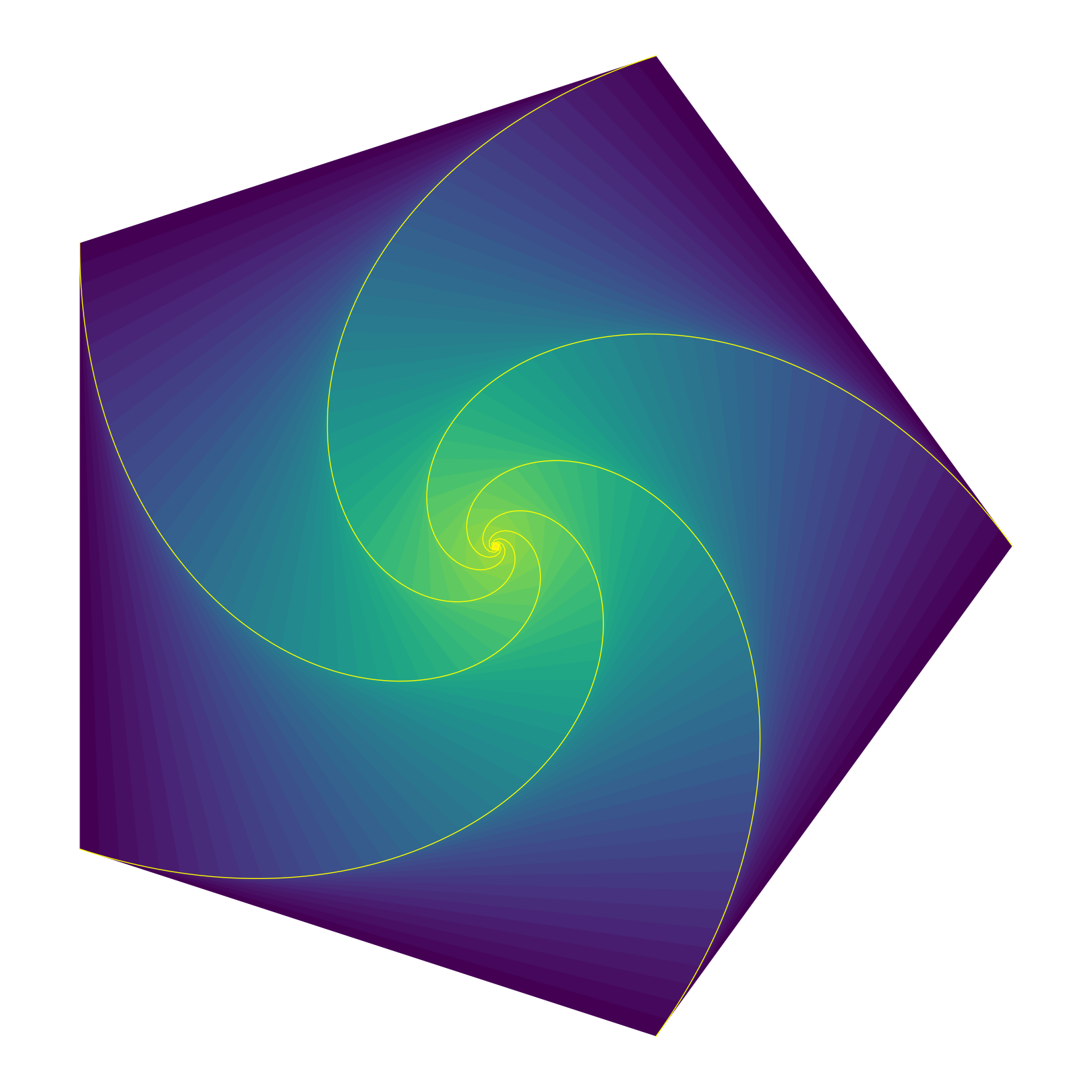
$n$ tortues sont disposées sur les sommets d’un polygone régulier à $n$ côtés. Au top départ, chacune se met à poursuivre à vitesse constante sa voisine dans le sens trigonométrique jusqu’à ce qu’elles se rejoignent toutes au centre.
On remarque que le polygone formé par les tortues est à tout moment une réduction et rotation du polygone de départ.
Utilisons les coordonnées polaires $(r(t);\theta(t))$ pour décrire une des tortues dont la position initiale servira d’origine des angles $(r(0)=r;\theta(0)=0).$
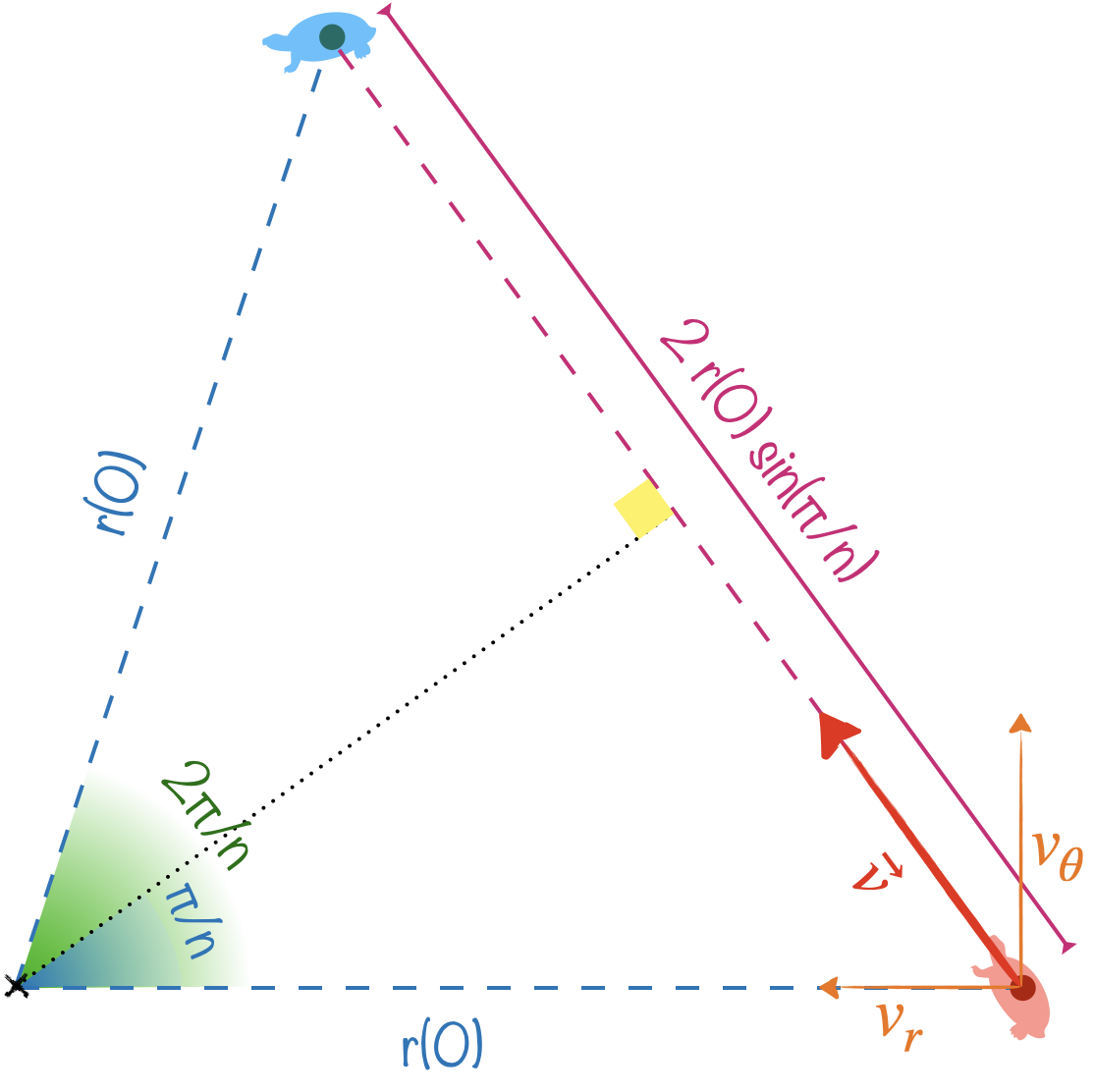
$\displaystyle v_r = \frac{dr}{dt} = -v\sin\left(\frac{\pi}{n}\right)$
$\displaystyle v_\theta = r\frac{d\theta}{dt} = v\cos\left(\frac{\pi}{n}\right)$
En jouant un peu avec ces deux expressions, on obtient :
$\displaystyle \frac{v}{r}\cos\left(\frac{\pi}{n}\right) = \frac{d\theta}{dt} = \frac{d\theta}{dr} \cdot\frac{dr}{dt} = -\frac{d\theta}{dr}v\sin\left(\frac{\pi}{n}\right)$
On peut simplifier par $v$, ce qui donne :
$\displaystyle \frac{dr}{d\theta} = -r\frac{\sin(\pi/n)}{\cos(\pi/n)} = -r\tan\left(\frac{\pi}{n}\right)$
Et finalement :
$\displaystyle \frac{dr}{r} = - \tan\left(\frac{\pi}{n}\right) d\theta$
Ce qui s’intègre en une belle spirale logarithmique :
$\displaystyle r(\theta) = r(0)\exp\left(-\theta\tan\left(\frac{\pi}{n}\right)\right)$
Cherchons maintenant le temps mis par les tortues pour rejoindre le centre du polygone :
$\displaystyle T=\int_0^T dt = \int_{r(0)}^0 \frac{dr}{(dr/dt)}=\int_{r(0)}^0\frac{dr}{-v\sin(\pi/n)}$
D’où $\displaystyle T = \frac{1}{v}\int_0^{r(0)}\frac{dr}{\sin(\pi/n)} = \frac{r(0)}{v \sin(\pi/n)}$
Et la distance parcourue vaut donc $\displaystyle D = \frac{r(0)}{ \sin(\pi/n)}$.
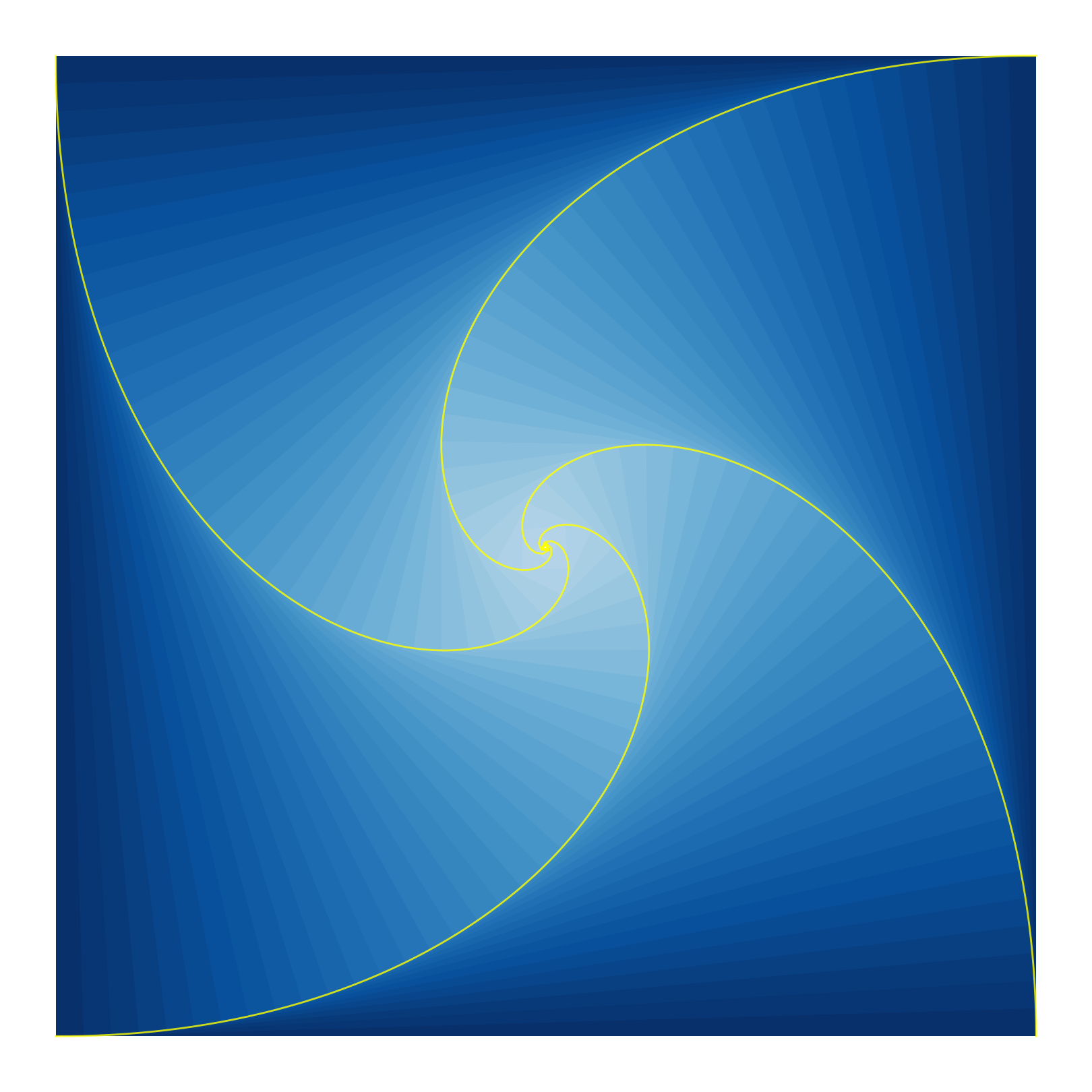
Dans le cas d’un carré, les expressions deviennnent encore plus simples :
$\displaystyle r(\theta) = r(0)\exp\left(-\theta \right)$
Et $\displaystyle D = r(0)\frac{\sqrt{2}}{2} = a$, en appelant $a$ le côté du carré. Donc le long de leur spirale, les tortues parcourent au final la longueur d’un côté du carré initial.
On peut expliquer ça simplement par le fait que la vitesse relative entre deux tortues restent en permanence identique à $v$ puisque leurs vecteurs vitesse sont à tout moment orthogonaux.
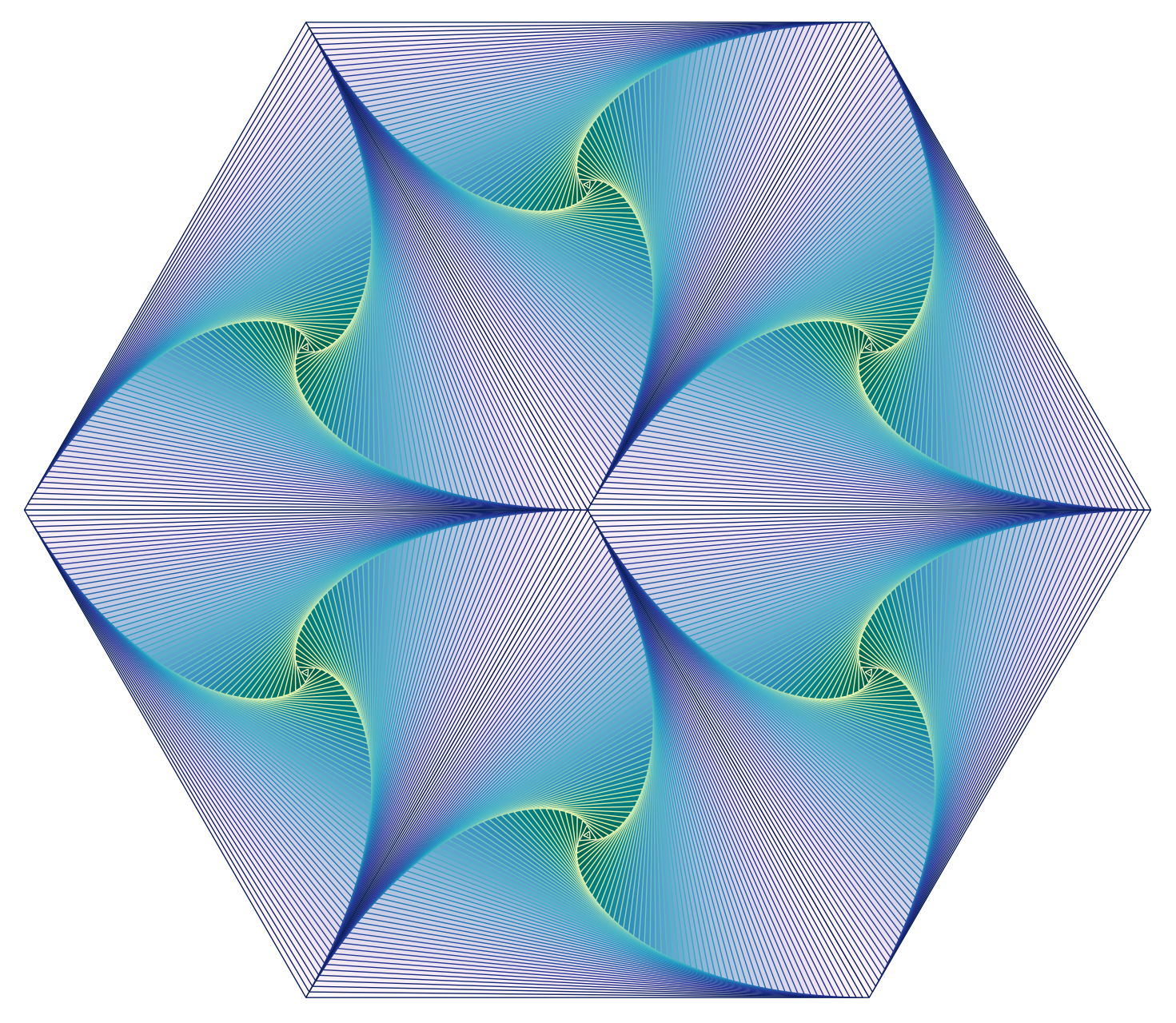
On peut s’amuser à combiner les poursuites pour faire des jolies figures… Ci-dessous, on assemblé 6 poursuites à 3 tortues pour former un hexagone.
Murmurations
Comme le montre cette très chouette vidéo de fouloscopie, nos histoires de poursuite participent à l’explication des comportements collectifs fascinants des bancs de possions ou des murmurations d’étourneaux. Un poisson (ou oiseau) ne ferait en fait que poursuivre les quelques individus immédiatement dans son champ de vision.
Le code suivant utilise les 6 premiers voisins et permet de voyager un peu dans le diagramme de phase.