Cercle et triangle
Trigonométrie

La loi des sinus a contribué à la définition du mètre, la première unité “universelle” lors de la révolution française.
Delambre et Méchain furent missionner pour mesurer le plus précisément possible un bout de méridien entre Dunkerque et Barcelone, la toute neuve définition du mètre étant :
un mètre est la dix millionième partie d’un quart de méridien terrestre
Le cercle répétiteur de Borda fut leur arme secrète. Il permettait alors de mesurer des angles avec une incertitude de quelques secondes seulement. Mesurer des distances avec cette précision est beaucoupl plus difficile ! L’idée fut alors de réaliser des triangulations : on vise des sommets faciles à repérer et on note les angles entre eux. Ils réalisèrent des dizaines de visées tout le long du bout de méridien étudié et le recouvrit de triangles.
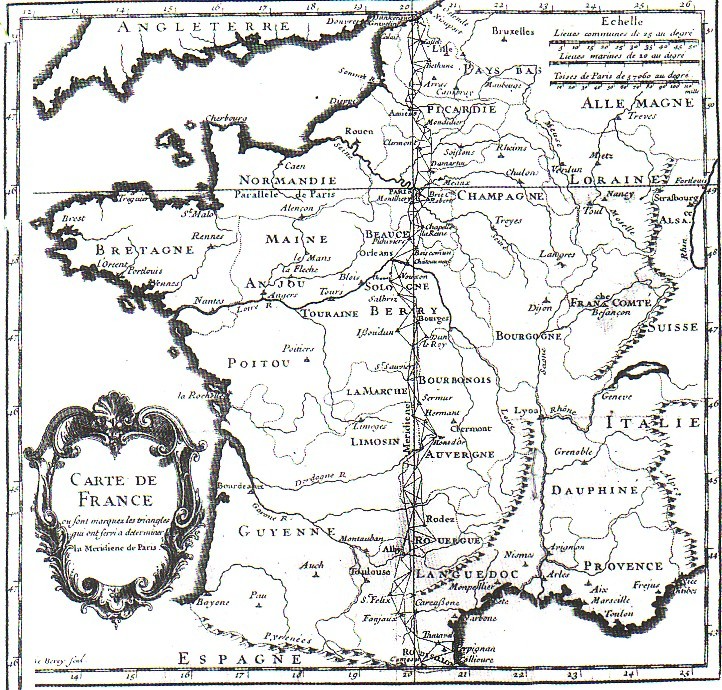
Une seule distance mesurée avec une grande précision permit alors de déterminer toutes les autres. En effet, grâce à la loi des sinus, la connaissance de la longueur d’un côté et de deux angles dans un triangle permet de déterminer les longueurs des deux autres côtés.
Thalès l’avait semble-t-il déjà réalisé puisqu’il aurait mis au point la méthode suivante pour connaître la distance entre un navire et la côte : deux observateurs $A$ et $C$ s’éloignent en direction opposée le long du trait de côte et mesurent les angles $\alpha = \widehat{CAB}$ et $\gamma = \widehat{ACB}$ entre la direction du bateau et la côte ainsi que la distance $AC$ qui les sépare l’un de l’autre. On a alors $d=AC\times\frac{\sin\left(\gamma\right)\sin\left(\alpha\right)}{\sin\left(\pi-(\alpha+\gamma)\right)}$ !
Preuve :
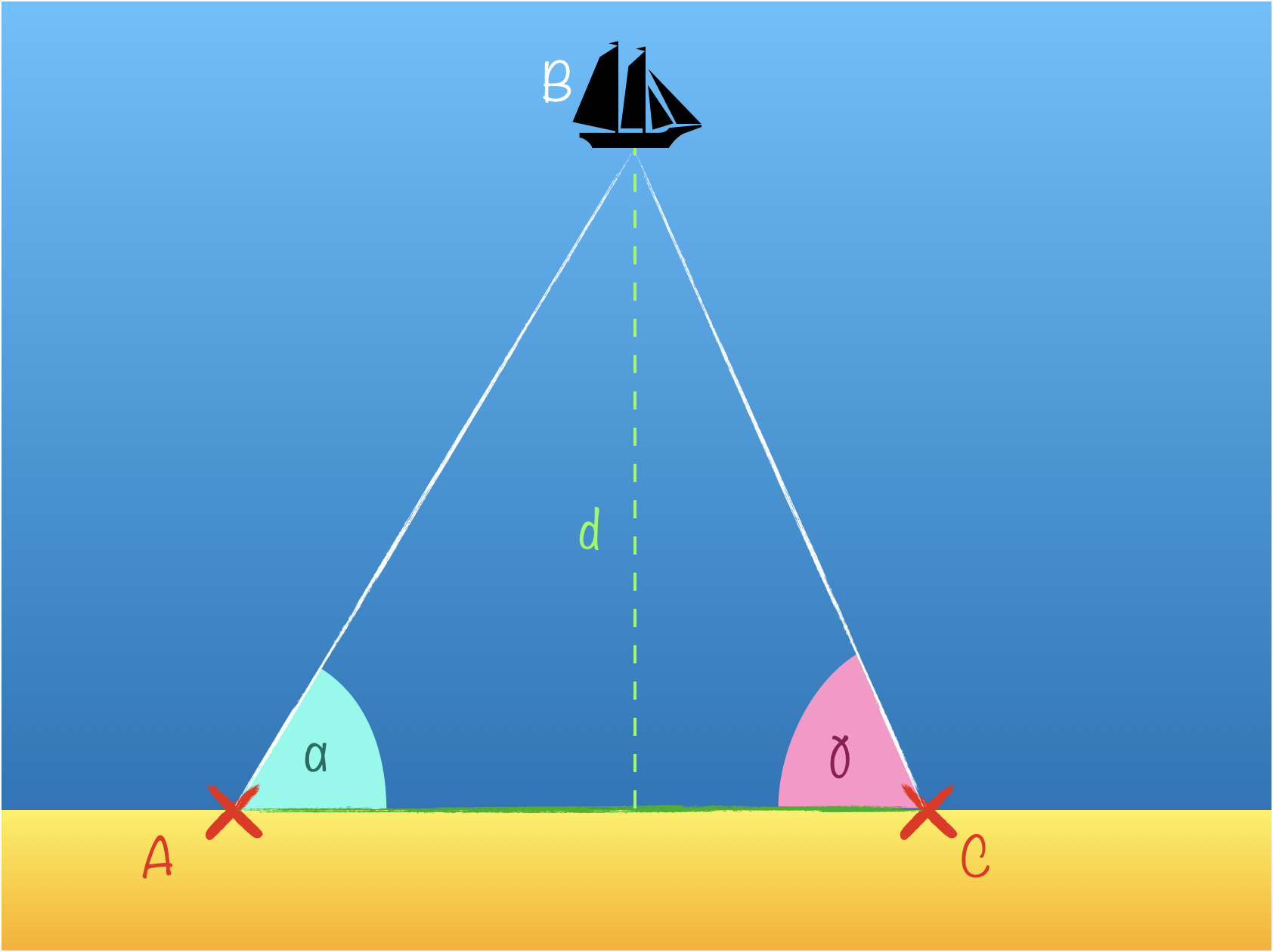
$$\beta=180^\circ - (\alpha+\gamma)$$ $$AB = AC\times\frac{\sin\gamma}{\sin\beta}$$ $$d=AB\sin\alpha$$
Théorème de l’angle inscrit et de l’angle au centre
Nom d’un théorème et système éducatif :
L’éducation secondaire se démocratise au cours du xixe siècle. La géométrie, qui a souvent pour but d’exercer à la logique, en est un élément important. Les manuels se répandent, et leurs auteurs se mettent à introduire plus ou moins systématiquement des éléments historiques, en particulier en attribuant des noms de mathématicien aux théorèmes. L’époque est également au renouveau des recherches historiques sur les mathématiques de la Grèce antique. C’est dans ce contexte qu’à partir de la fin du xixe siècle le nom de Thalès est attribué à deux théorèmes distincts. En France puis en Italie c’est à un théorème du livre VI des Éléments d’Euclide, soit celui sur la proportionnalité des segments découpés par une ligne parallèle à un côté dans un triangle, soit sa généralisation pour deux sécantes. En Allemagne c’est au théorème de l’angle inscrit dans un demi-cercle. Ces dénominations sont bien établies dans les années 1920, époque à laquelle d’autres pays adoptent l’une ou l’autre (mais pas l’Angleterre ni les États-Unis).
Ces choix correspondent à des traditions différentes d’enseignement de la géométrie, plutôt fidèle à Euclide et à l’ordre d’exposition des Éléments en Allemagne, alors qu’une tradition plus anti-euclidienne s’est développée en France depuis La Ramée. Le choix s’est porté en France et en Italie, sur un théorème qui met en évidence un invariant de la géométrie affine, le rapport de mesures algébriques sur une droite, ce qui correspond au développement en Europe de la géométrie projective et affine au xixe siècle. Ce théorème est mis en avant dans les débuts de l’apprentissage de la géométrie, alors que l’Allemagne privilégie le théorème de Pythagore, et choisit de donner le nom de Thalès à un théorème lié au triangle rectangle.
Dans un cas comme dans l’autre, le choix du nom n’a finalement pas obéi a des considérations strictement historiques. L’histoire est instrumentalisée au service d’un choix didactique : il s’agit de mettre un théorème en avant, en lui attribuant le nom d’un mathématicien célèbre, d’où des choix différents dans des traditions d’enseignement différentes.
Source : Wikipédia