
Notes de lecture du livre La logique pas à pas de Jacques Duparc que je paraphrase allégrement.
Logique modale

Une petite communauté de dragons vivent sur une île aux règles spéciales. Si un dragon apprend qu’il a les yeux bleus, c’est la honte et il doit partir le soir même. Mais les autres dragons n’ont pas le droit de lui dire et aucun de ces dragons n’a de reflet et ne peut donc constater la couleur de ses propres yeux.
Trois dragons peuplent l’île, Apophis, Bahamut et Caraxès, lorsqu’un jour, un étranger débarque.
L’étranger déclare :
l’un de vous au moins a les yeux bleus.
Le premier soir, aucun dragon ne part.
Le deuxième soir, toujours rien.
Le troisième soir, ils partent tous les trois…
La logique modale va permettre de modéliser ce petit problème.
Syntaxe
La syntaxe de la logique modale est celle du calcul des propositions à laquelle on ajoute deux opérateurs unaires, les opérateurs de modalité :
- La boite $\Box$
- Le diamant $\Diamond$
On va être amené à non pas définir un seul $\Box$ et $\Diamond$ mais potentiellement une infinité (dénombrable).
On écrira alors $[i]$ et $\langle i \rangle$, où $i$ varie dans un ensemble $I$.
Le langage $\mathcal{L}$ de la logique modale est l’ensemble suivant :
$\mathcal{L}=VAR\cup\set{\top,\bot,\neg,\lor,\land\rightarrow,\leftrightarrow,(,)}\cup\set{[i]:i\in\mathbb{N}}\cup\set{\langle i\rangle:i\in\mathbb{N}}$
Soient $\phi$, $\psi$, $\theta$ trois formules, on note $\phi[\theta/\psi]$ la substitution uniforme de la formule $\theta$ à toutes les occurrences de $\psi$ dans $\phi$.
Une substitution uniforme consiste dans un premier temps à retirer toutes les occurrences de $\psi$ puis à remplacer chacune par $\theta$.
Sémantique
Système de transition
On va utiliser les modèles de Kripke, c’est-à-dire des graphes dirigés, pour interpréter les formules de la logique modale. Mais on se cantonnera ici à la logique classique (les interprétations de la négation et de l’implication seront traditionnels et non intuitionnistes). Chaque nœud va correspondre à des mondes possibles qui sont ou non liés entre eux par des arcs.
On appelle ces graphes dirigés des systèmes de transition (frame en anglais) :
Pour $I$ un ensemble non vide, un système de transition étiqueté par $I$ (ou de signature $I$) est une structure relationnelle (un graphe dirigé étiqueté)
$$\mathcal{S}=(N,A)$$
où $N$ est un ensemble non vide dont les éléments sont appelés nœuds
et $A$ est un ensemble de ralations binaires sur $\mathbb{N}$ indicées par $I$ ($A=\set{A_i\subseteq N\times N|i\in I}$).
Un système de transition $\mathcal{S}(N,A)$ (avec $A=\set{A_i\subseteq N\times N|i\in I}$) est dit
- réflexif si, pour tout $i\in I$ et pour tout $a\in N$, il vérifie $a\xrightarrow{i}a$ ;
- symétrique si, pour tout $i\in I$ et pour tout $a,b\in N$, dès qu'il vérifie $a\xrightarrow{i}b$, il vérifie aussi $b\xrightarrow{i}a$ ;
- transitif si, pour tout $i\in I$ et pour tout $a,b,c\in N$, dès qu'il vérifie à la fois $a\xrightarrow{i}b$ et $b\xrightarrow{i}c$, il vérifie aussi $a\xrightarrow{i}c$ ;
- famélique si, pour tout $i\in I$ et pour tout $a,b\in N$, dès qu'il vérifie $a\xrightarrow{i} b$ alors $a=b$ ;
- dense si, pour tout $i\in I$ et pour tout $a,c\in N$, dès qu'il vérifie $a\xrightarrow{i} c$, alors il existe $b$ tel que $a\xrightarrow{i} b$ et $b\xrightarrow{i} c$ ;
- non borné à droite si, pour tout $i\in I$ et pour tout $a\in N$, il existe un nœud $b\in N$ tel que $a\xrightarrow{i}b$ ;
- euclidien si, pour tout $i\in I$ et pour tout $a,b,c\in N$, dès qu'il vérifie à la fois $a\xrightarrow{i} b$ et $a\xrightarrow{i} c$, alors il vérifie aussi $b\xrightarrow{i} c$.
Satisfaction
Un système de transition se mue en modèle de la logique modale (modèle de Kripke) dès qu’il est équipé d’une valuation portant sur les variables étudiées. Une valuation indique pour chaque nœud du graphe les variables qui sont forcées en ce nœud.
Soient $I$ un ensemble non vide et $\mathcal{S}=(N,A)$ un système de transition étiqueté par $I$.
Une valuation sur ce système de transition $\mathcal{S}$ est une fonction :
$$
\begin{array}{ccc}
\mathcal{V}: VAR & \to & \mathcal{P}(N)\\
\phantom{\mathcal{V}:}P & \mapsto & \set{a|a\Vdash P}
\end{array}
$$
La satisfaction d’une formule $\phi$ au nœud $a$ (au sein de $\mathcal{S}$ et pour la valuation $\mathcal{V}$) est notée $a\Vdash\phi$ et se définit par induction sur la hauteur de $\phi$ :
- $a\Vdash\top$ et $a\nVdash\bot$
- $a\Vdash P$ ssi $a\in\mathcal{V}(P)$ (pour une variable $P$ quelconque)
- $a\Vdash\neg\phi$ ssi $a\nVdash\phi$
- $a\Vdash\phi\lor\psi$ ssi ($a\Vdash\phi$ ou $a\Vdash\psi$)
- $a\Vdash\phi\land\psi$ ssi ($a\Vdash\phi$ et $a\Vdash\psi$)
- $a\Vdash\phi\rightarrow\psi$ ssi ($a\nVdash\phi$ ou $a\Vdash\psi$)
- $a\Vdash\phi\leftrightarrow\psi$ ssi (($a\Vdash\phi$ et $a\Vdash\psi$) ou ($a\nVdash\phi$ et $a\nVdash\psi$))
- $a\Vdash[i]\phi$ ssi pour tout $b$, si $a\xrightarrow{i}b$, alors $b\Vdash\phi$
- $a\Vdash\langle i\rangle\phi$ ssi il existe $b$ tel que $a\xrightarrow{i}b$ et $b\Vdash\phi$
-
S’il n’existe pas de nœud $b$ tel que $a\xrightarrow{i}b$, alors quelle que soit la formule $\phi$, $a\Vdash\langle i\rangle\phi$ est toujours fausse. Autrement dit, $a\nVdash \langle i\rangle\phi$.
-
Par contre, s’il n’existe pas de nœud $b$ tel que $a\xrightarrow{i}b$, alors $a\Vdash[i]\phi$ est toujours vraie quelle que soit la formule $\phi$. En effet pour que $a\Vdash[i]\phi$ soit vérifiée il faut que si $a\xrightarrow{i}b$, alors $b\Vdash\phi$. Mais s’il n’y a aucun $a\xrightarrow{i}b$ alors l’implication est tojours vérifiée.
La satisfaction d’une formule en un nœud $a$ d’un système de transition $\mathcal{S}$ équipé d’une valuation $\mathcal{V}$ dépend de ces trois ingrédients et on notera donc $\langle \mathcal{S},\mathcal{V},a\rangle\Vdash\phi$.
Revenons à nos dragons :
Exemple des dragons aux yeux bleus
les mondes possibles (les nœuds du graphe) vont correspondre aux différentes combinaisons possibles de couleurs d’yeux pour les trois dragons $A$, $B$ et $C$. On a deux possibilités (yeux bleus ou non) pour chacun des trois dragons. Cela fait 8 mondes possibles.
Les arcs entre mondes vont être étiquetés chacun par un des trois dragons et vont correspondre aux différents mondes que ce dragon pense possible depuis le monde où il est.

Par exemple, dans le monde où seul $B$ a les yeux bleus (le monde 3) $A$ imagine aussi possible le monde où $A$ et $B$ ont tous les deux les yeux bleus (le monde 5). Une flèche étiquetée par $A$ rejoint donc ces deux mondes possibles. Et bien sûr, dans le monde où $A$ et $B$ ont les yeux bleus, $A$ imagine possible le monde où seul $B$ a les yeux bleus (il y a donc une flèche de 5 vers 3). Et comme c’est vrai dans chaque cas et pour les trois dragons, cela montre que ce système de transition est symétrique. Il est de plus évident que chaque monde semble possible pour les dragons qui s’y trouvent. Le système est donc aussi réflexif.
Imaginons que l’on soit dans le monde 2. L’ensemble des mondes possibles se simplifient alors grandement.
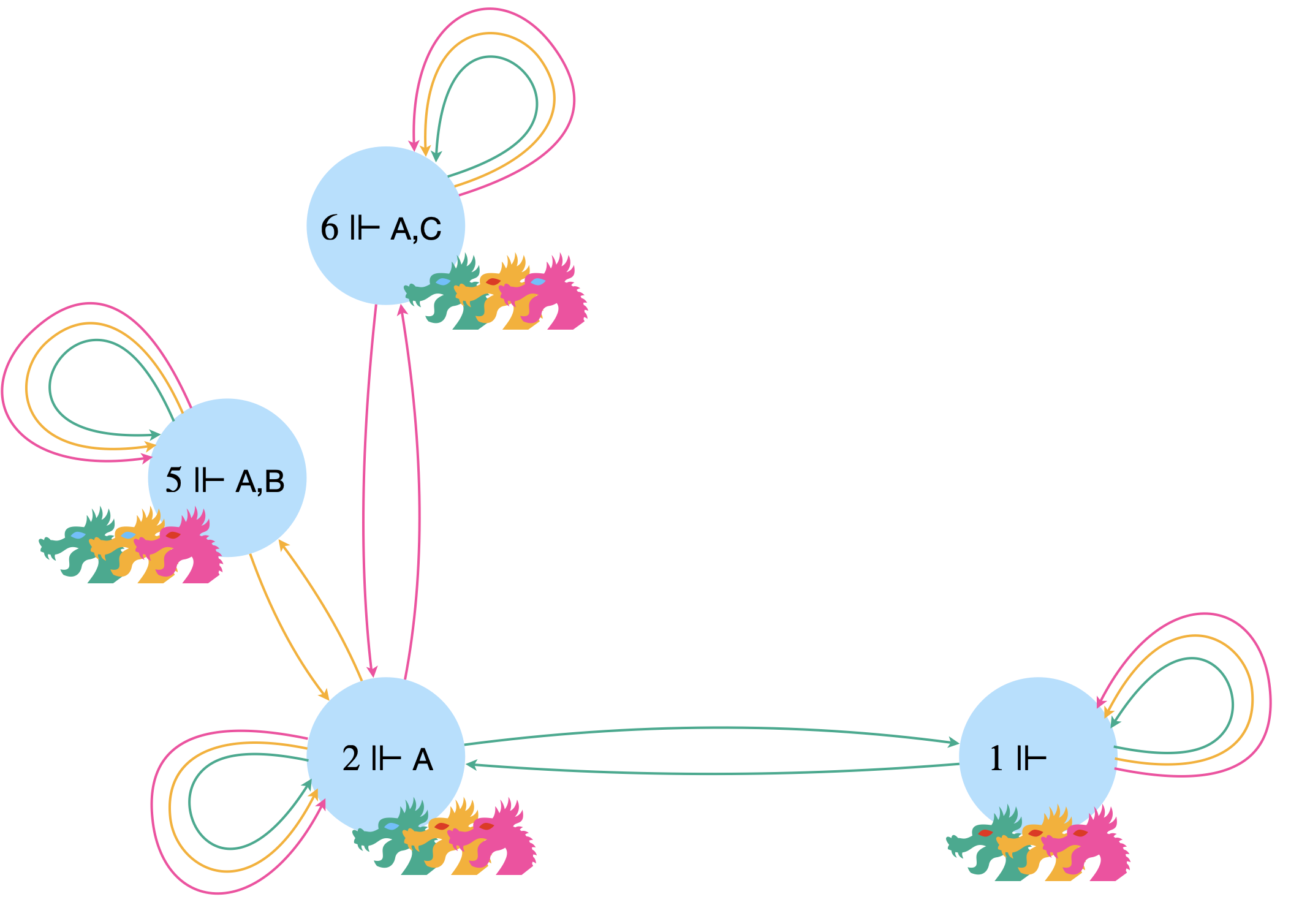
La déclaration de l’étranger n’est pas une surprise pour $B$ et $C$ qui voient bien que le pauvre $A$ a les yeux bleus et est donc sans effet pour eux. Par contre $A$ comprend que l’autre monde qu’il pensait possible, le monde béni où il n’avait pas des yeux infames (le monde 1) est en fait impossible.
Avant la déclaration de l’étranger, $2\Vdash\color{#00AB8E}\langle A\rangle \color{#000}\neg A$ puisqu’il y a une flèche étiquetée par $A$ qui rejoint 1 (qui réalise $\neg A$). On peut traduire ça par : “dans le monde 2, Apophis croit possible qu’il n’ait pas les yeux bleus”. De même $2\Vdash\color{#FEAE00}\langle B\rangle \color{#000}\neg B$ à cause de la flèche étiquetée par $B$ vers le monde 5 et $2\Vdash\color{#FF42A1}\langle C\rangle \color{#000}\neg C$ à cause de la flèche étiquetée par $C$ vers le monde 6. Donc chaque dragon croit encore possible d’avoir les yeux bleus.
D’autre part, on peut écrire que $2\Vdash\color{#FF42A1}[C] \color{#000} A$ puisque les trois arcs étiquetés par $C$ qui partent de 2 vont dans des mondes (2, 5 et 6) où $A$ est réalisée. Ça peut se lire : “dans le monde 2, Caraxès sait qu’Apophis a les yeux bleus”.
On peut aussi compliquer les énoncés avec par exemple : $6 \Vdash \color{#FF42A1}\langle C\rangle \color{#FEAE00}\langle B\rangle \color{#000} (B\land\neg C)$ (une flèche rose part de 6 vers 2 et une flèche jaune part de 2 vers 5 où $B$ a les yeux bleus mais pas $C$).
Après la déclaration de l’étranger, le monde 1 disparaît !
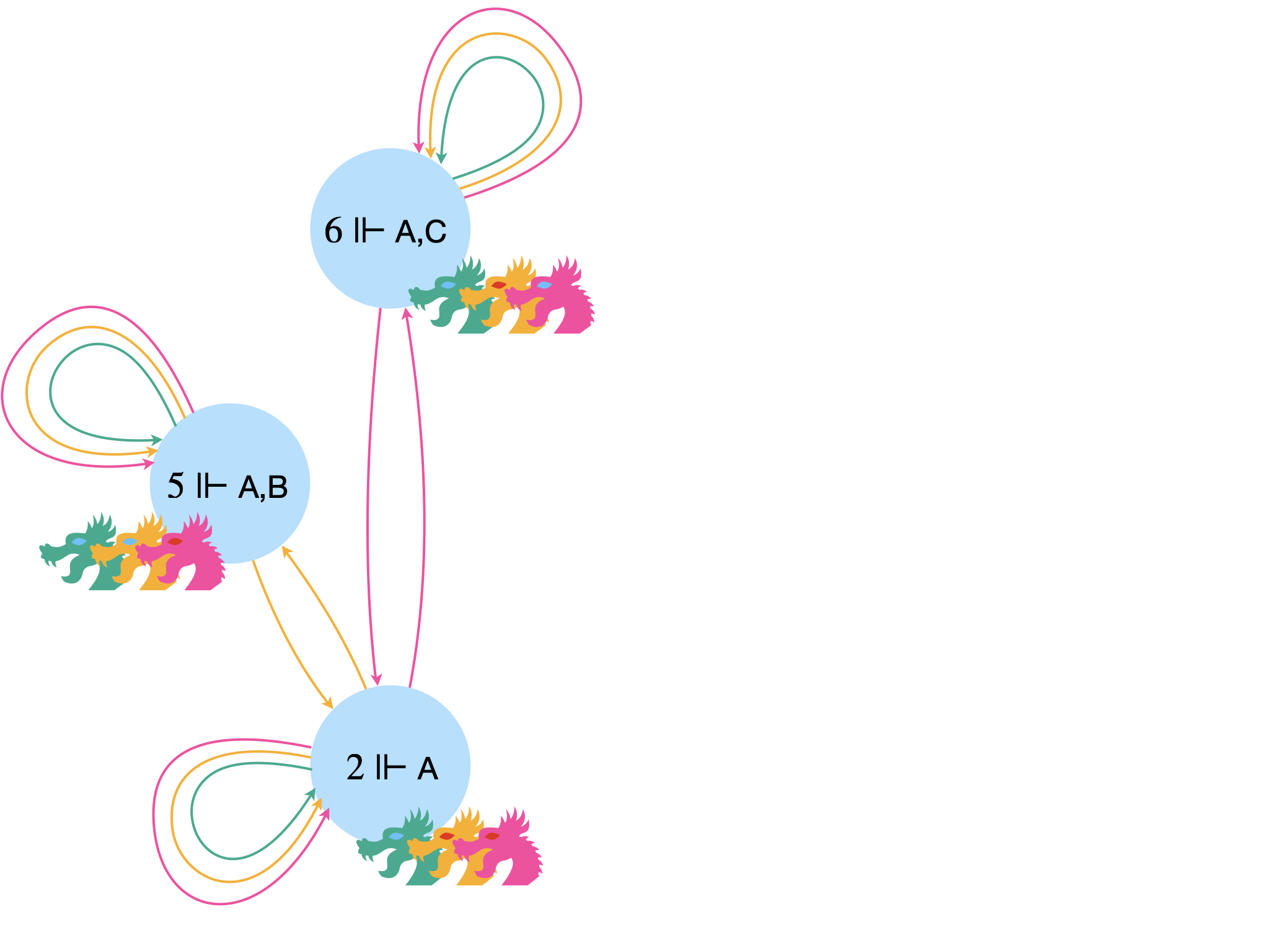
Si $B$ et $C$ sont toujours dans le doute quant à la couleur de leurs yeux, pour $A$, les jeux sont faits. En effet, on a dorénavant $2\Vdash\color{#00AB8E}[A] \color{#000} A$. Et le soir même, Apophis s’en va tout penaud.
En généralisant, dans les mondes où seul un dragon a les yeux bleus (2, 3 et 4), ce dragon le comprend au moment de la déclaration de l’étranger et se retire le soir même.
Imaginons maintenant que l’on soit dans le monde 5 où Apophis et Bahamut ont les yeux bleus.
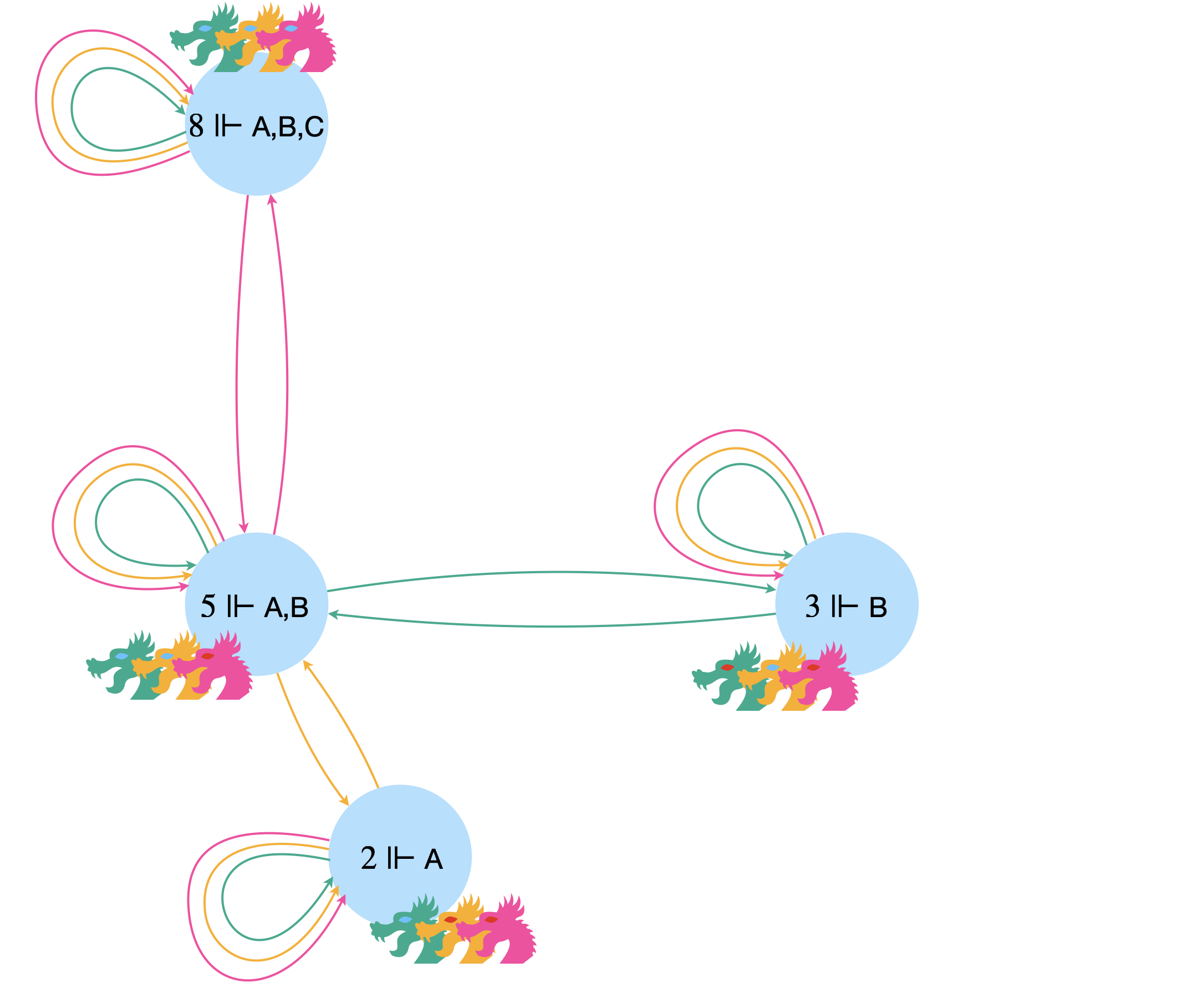
La déclaration de l’étranger ne fait pas beaucoup d’effet car ils étaient déjà tous les trois au courant qu’au moins l’un d’eux avait les yeux bleus… Par conséquent, le soir même, personne ne part. Et ça par contre, ça change pas mal de choses ! En effet, les mondes 2 et 3 deviennet d’un coup impossibles puisque on a vu que les mondes où seul un des dragon a les yeux bleus voient ce dragon décamper dès le premier soir.
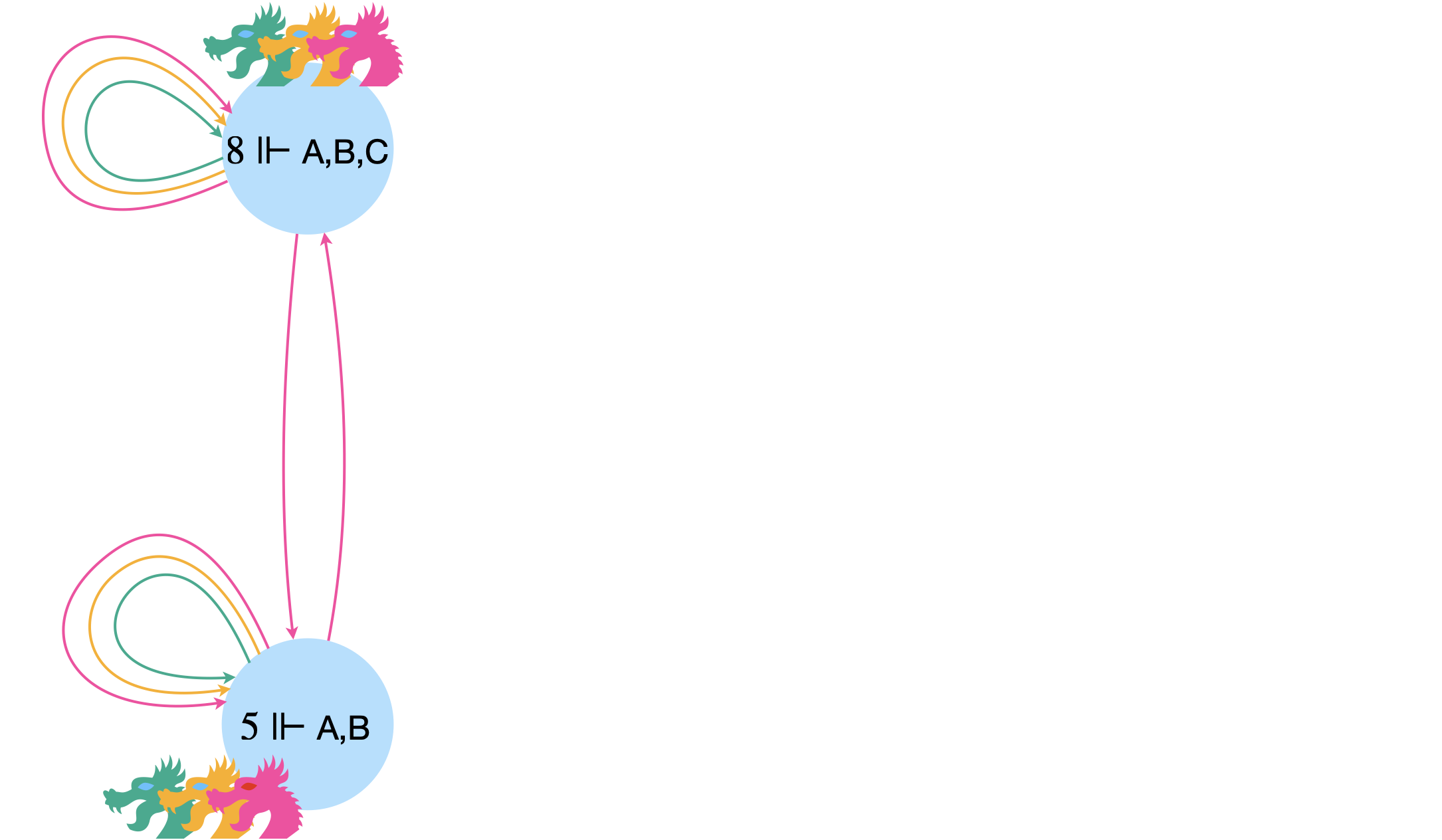
On a maintenant : $5\Vdash (\color{#00AB8E}[A] \color{#000} A)\land (\color{#FEAE00}[B] \color{#000} B)$. $A$ et $B$ ont acquis la certitude d’avoir les yeux bleus et s’envolent au deuxième soir.
Les deux dragons aux yeux bleus des mondes 7 ou 6 auraient fait de même.
La dernière situation possible correspond au monde 8.
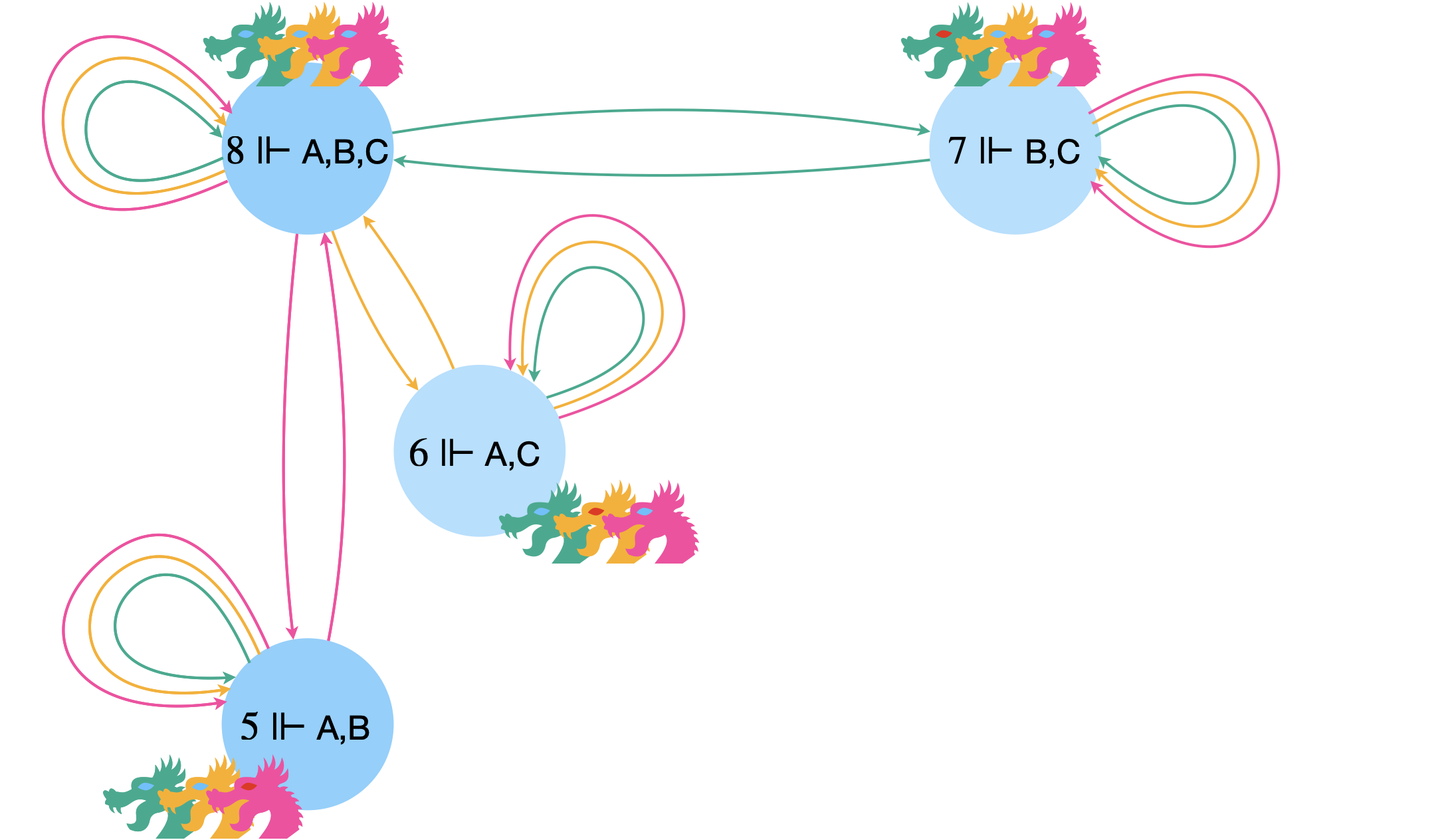
On reprend le raisonnement précédent. Personne ne part au premier soir, mais cette fois-ci, ça ne permet d’éliminer aucun monde possible… Et par conséquent, au deuxième soir, personne ne s’envole. Mais là, bingo ! Ça élimine les mondes où seuls deux dragons ont les yeux piscine. Finalement, ils comprennent tous les trois qu’ils sont banis et s’envolent au troisième soir.
La situation de départ correspondait donc au monde 8.
On peut remarquer en passant différentes équivalences :
- $a\Vdash\neg\color{#00AB8E}[A] \color{#000} \phi$ ssi $a\Vdash \color{#00AB8E}\langle A\rangle \color{#000} \neg \phi$
Pour A, ne pas savoir quelque chose est équivalent à croire possible sont contraire. - $a\Vdash\color{#00AB8E}[A] \color{#000} \phi$ ssi $a\Vdash \neg\color{#00AB8E}\langle A\rangle \color{#000} \neg \phi$
Pour A, savoir quelque chose est identique à ne pas croire possible le contraire de cette chose. - $a\Vdash\neg\color{#00AB8E}[A] \color{#000} \neg\phi$ ssi $a\Vdash \color{#00AB8E}\langle A\rangle \color{#000} \phi$
Pour A, croire possible quelque chose revient à ne pas savoir le contraire de cette chose.
Modèles et classes
Soient $\phi$ une formule, $I$ un ensemble non vide, $\mathcal{S}=(N,A)$ un système de transition étiqueté par $I$, $a$ un nœud de $\mathcal{S}$ et $\mathcal{V}$ une valuation,
- $\langle\mathcal{S},\mathcal{V}\rangle\Vdash^{\forall a}\phi$ ssi pour tous nœuds $a'$, $\langle\mathcal{S},\mathcal{V},a'\rangle\Vdash\phi$
- $\langle\mathcal{S},a\rangle\Vdash^{\forall \mathcal{V}}\phi$ ssi pour toutes valuations $\mathcal{V'}$, $\langle\mathcal{S},\mathcal{V'},a\rangle\Vdash\phi$
- $\mathcal{S}\Vdash^{\forall a,\forall \mathcal{V}}\phi$ ssi pour tous nœuds $a'$ et toutes valuations $\mathcal{V'}$, $\langle\mathcal{S},\mathcal{V'},a'\rangle\Vdash\phi$
Un modèle de la logique modale (modèle de Kripke) est un système de transition équipé d’une valuation : $$\mathcal{M}=\langle\mathcal{S},\mathcal{V}\rangle$$ Une formule $\phi$ est vraie (ou satisfaite) dans le modèle $\langle\mathcal{S},\mathcal{V}\rangle$ si elle est forcée en chacun des nœuds du système de transition : $$\langle\mathcal{S},\mathcal{V}\rangle\Vdash^{\forall a}\phi$$
La notion de vérité dans un modèle de Kripke est donc une notion de vérité globale puisqu’elle prend en compte l’ensemble des nœuds du système de transition.
Prenons l’exemple du système de transition $\mathcal{S}$ équipé de la valuation $\mathcal{V}$ ci-dessous :
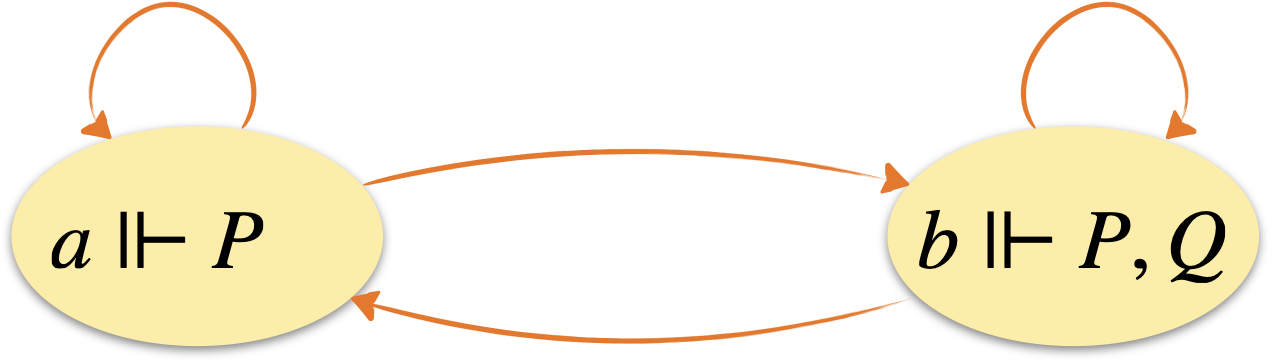
On a bien $\langle\mathcal{S},\mathcal{V}\rangle\Vdash^{\forall a}Q\lor\neg Q$. Par contre, comme $b\Vdash Q$ alors que $a\Vdash\neg Q$, $\langle\mathcal{S},\mathcal{V}\rangle\nVdash^{\forall a}Q$ et $\langle\mathcal{S},\mathcal{V}\rangle\nVdash^{\forall a}\neg Q$.
On peut donc avoir une formule $\phi\lor\psi$ satisfaite sans que ni $\phi$ ni $\psi$ ne le soit !
On retrouve les modèles du calcul des propositions en se restreignant aux systèmes de transition contenant un seul nœud. Dit autrement, une formule $\phi$ de profondeur modale nulle est une formule du calcul des propositions.
Soit $\mathcal{M}$ un modèle du calcul des propositions défini par la distribution de valeur de vérité $\delta_\mathcal{M}$ qui associe aux variables apparaissant dans $\phi$ la valeur 1 lorsqu’elles sont vraies dans $\mathcal{M}$ et 0 sinon ($\delta_\mathcal{M}(P)=1$ ssi $\mathcal{M}\models P$). La formule $\phi$ st vraie dans $\mathcal{M}$ (noté $\mathcal{M}\models\phi$) si et seulement si cette même formule $\phi$ est vraie dans le système de transition $\mathcal{S}_\mathcal{M}=(N,A)$, où $N=\set{a}$ et $A=\empty$, équipé de la valuation $\mathcal{V}_{\delta_\mathcal{M}}$ définie par : $\mathcal{V}_{\delta_\mathcal{M}}(P)=\set{a}$ si et seulement si $\delta_\mathcal{M}(P)=1$ et $\mathcal{V}_{\delta_\mathcal{M}}(P)=\empty$ si et seulement si $\delta_\mathcal{M}(P)=0$.
Cela s’écrit : $\mathcal{M}\models\phi$ ssi $\langle\mathcal{S},\mathcal{V}_{\delta_\mathcal{M}}\rangle\Vdash^{\forall a}\phi$
Soit $\phi$ une formule de la logique modale et $\mathcal{S}$ un système de transition.
La formule $\phi$ est valide dans $\mathcal{S}$ si :
$$\mathcal{S}\Vdash^{\forall a,\forall \mathcal{V}} \phi$$
La notion de validité est globale, elle aussis. Et à nouveau, une formule $\phi\lor\psi$ peut être valide dans un système de transition sans que ni $\phi$, ni $\psi$ ne le soit.
Soient $\phi$ une formule de profondeur modale nulle et $\mathcal{S}=(N,A)$ un système de transition.
Les affirmations suivantes sont équivalentes :
- $\mathcal{S}\Vdash^{\forall a,\forall\mathcal{V}} \phi$
- Il existe $a\in N$ tel que $\langle\mathcal{S},a\rangle\Vdash^{\forall \mathcal{V}}\phi$
- Pour $\mathcal{T}=(\set{a},\empty)$, $\langle\mathcal{T},a\rangle\Vdash^{\forall \mathcal{V}}\phi$
- $\phi$ est une tautologie du calcul des propositions
On va montrer la suite des implications suivante $(1)\rightarrow(2)$, $(2)\rightarrow(3)$, $(3)\rightarrow(4)$ et $(4)\rightarrow(1)$. La circularité nous permettra alors d’obtenir toutes les autres implications. Par exemple, $(2)\rightarrow(1)$ découle de $(2)\rightarrow(3)\rightarrow(4)\rightarrow(1)$.
- $(1)\rightarrow(2)$ et $(2)\rightarrow(3)$ sont immédiates.
- Pour montrer $(3)\rightarrow(4)$, nous allons montrer la contraposée $\neg(4)\rightarrow\neg(3)$.
Supposons que $\phi$ n'est pas une tautologie du calcul des propositions. Il existe donc un modèle $\mathcal{M}$ pour lequel la formule est fausse. Équipons alors le système de transition $\mathcal{T}=(\set{a},\empty)$ de la valuation où pour chacune des variables propositionnelles $P$ apparaissant dans $\phi$, $a\in\mathcal{V}(P)$ si et seulement si $\mathcal{M}\models P$.
Par définition de la satisfaction locale d'une formule $\langle \mathcal{T},\mathcal{V},a\rangle\Vdash \phi$ ssi $\mathcal{M}\models\phi$.
Comme notre hypothèse est que $\mathcal{M}\not\models\phi$, on en déduit que $\langle \mathcal{T},\mathcal{V},a\rangle\nVdash \phi$. On a donc trouvé une valuation qui contredit $(3)$. - Pour montrer $(4)\rightarrow(1)$, on passe également par la contraposée $\neg(1)\rightarrow\neg(4)$.
On suppose que $\mathcal{S}\Vdash^{\forall a,\forall \mathcal{V}}\phi$ n'est pas satisfaite, et donc qu'il existe une valuation $\mathcal{V}$ et un nœud $a$ tels que $\langle\mathcal{S},\mathcal{V},a\rangle\nVdash\phi$. On définit le modèle du calcul des propositions $\mathcal{M}$ par $\mathcal{M}\models P$ si et seulement si $a\in\mathcal{V}(P)$, et ce pour chaque variable propositionnelle apparaissant dans $\phi$. On a donc $\mathcal{M}\not\models\phi$. Par conséquent, $\phi$ n'est pas une tautologie.
Soit $\phi$ une formule et $\mathscr{C}$ une classe de systèmes de transition.
$\mathscr{C}\Vdash\phi$ ssi pour tout $\mathcal{S}\in\mathscr{C}, \mathcal{S}\Vdash^{\forall a,\forall\mathcal{V}}\phi$ ($\phi$ est valide dans tout système de la classe $\mathscr{C}$).
Soit $\mathscr{C}$ la classe de tous les systèmes de transition.
$\mathscr{C}\Vdash\Box(P\rightarrow Q)\rightarrow(\Box P\rightarrow \Box Q)$
Soient $\mathcal{S}$ un système de transition, $a$ un nœud de $\mathcal{S}$ et $\mathcal{V}$ une valuation quelconque.
Si $\langle \mathcal{S},\mathcal{V}, a\rangle\Vdash\Box(P\rightarrow Q)$, alors pour tout $b$ tel que $a\longrightarrow b$, $\langle \mathcal{S},\mathcal{V}, b\rangle\Vdash P\rightarrow Q$.
Pour montrer $\langle \mathcal{S},\mathcal{V}, a\rangle\Vdash\Box P\rightarrow \Box Q$, il suffit de supposer $\langle \mathcal{S},\mathcal{V}, a\rangle\Vdash\Box P$ et de montrer $\langle \mathcal{S},\mathcal{V}, a\rangle\Vdash\Box Q$.
Or, si $\langle \mathcal{S},\mathcal{V}, a\rangle\Vdash\Box P$, alors $\langle \mathcal{S},\mathcal{V}, b\rangle\Vdash P$ pour tout $b$ tel que $a\longrightarrow b$. Et comme par hypothèse $\langle \mathcal{S},\mathcal{V}, b\rangle\Vdash P\rightarrow Q$, on en déduit $\langle \mathcal{S},\mathcal{V}, b\rangle\Vdash Q$.
Et comme c’est vrai pour tout $b$ successeur de $a$, on en déduit $\langle \mathcal{S},\mathcal{V}, a\rangle\Vdash\Box Q$.
Pour tout système de transition $\mathcal{S}$, les affirmations suivantes sont équivalents :
- $\mathcal{S}$ est réflexif
- Pour toute formule $\phi$, $\mathcal{S}\Vdash^{\forall a, \forall \mathcal{V}}(\Box\phi\rightarrow\phi)$
- $(1)\Rightarrow(2)$
Si un nœud $a$ quelconque, pour une valuation quelconque, vérifie $a\Vdash\Box \phi$, alors par définition, pour tout $b$ tel que $a\longrightarrow b$, $b\Vdash\phi$. Puisque $\mathcal{S}$ est réflexif, $a$ est lui-même un de ces $b$ et donc $a\Vdash\phi$. - $(2)\Rightarrow(1)$
Supposons que $\mathcal{S}$ ne soit pas réflexif. Il s'en suit qu'il existe un nœud $a$ tel que $a\,\,\not\!\!\longrightarrow a$. Soit $\phi=P$ une formule de hauteur nulle et $\mathcal{V}$ une valuation telle que $b\in\mathcal{V}(P)$ si et seulement si $a\longrightarrow b$. Par définition de $\mathcal{V}$, on a à la fois $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Box P$ et $\langle\mathcal{S},\mathcal{V},a\rangle\nVdash P$, donc $\langle\mathcal{S},\mathcal{V},a\rangle\nVdash (\Box P\rightarrow P)$. Cela prouve ainsi que $\mathcal{S}\nvdash ^{\forall a,\forall\mathcal{V}}(\Box P\rightarrow P)$, ce qui contredit l'hypothèse.
On note $\mathscr{C}_{ref.}$ la classe de tous les systèmes de transition réflexifs.
Pour tout système de transition $\mathcal{S}$, les affirmations suivantes sont équivalents :
- $\mathcal{S}$ est famélique
- Pour toute formule $\phi$, $\mathcal{S}\Vdash^{\forall a, \forall \mathcal{V}}(\phi\rightarrow\Box\phi)$
- $(1)\Rightarrow(2)$
Un système de transition $\mathcal{S}$ muni de la valuation $\mathcal{V}$ satisfait la formule $\phi\rightarrow\Box\phi$ au nœud $a$ si, $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\phi$ entraîne $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Box\phi$. Autrement dit, dès qu'une formule est satisfaite en un nœud, elle doit être satisfaite en chacun des successeurs de ce nœud.
Si le seul successeur possible d'un nœud est lui-même (système famélique), l'implication tient toujours. - $(2)\Rightarrow(1)$
Dans le cas où il existe un nœud $a$ possédant un successeur $b$ différent de lui-même, il suffit de considérer la formule $\phi=P$ et la valuation $\mathcal{V}$ qui vérifie $a\in\mathcal{V}(P)$ et $b\not\in\mathcal{V}(P)$ pour obtenir :
- $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\phi$
- $\langle\mathcal{S},\mathcal{V},a\rangle\nVdash\Box\phi$
- $\langle\mathcal{S},\mathcal{V},a\rangle\nVdash\phi\rightarrow\Box\phi$
Pour tout système de transition $\mathcal{S}$, les affirmations suivantes sont équivalents :
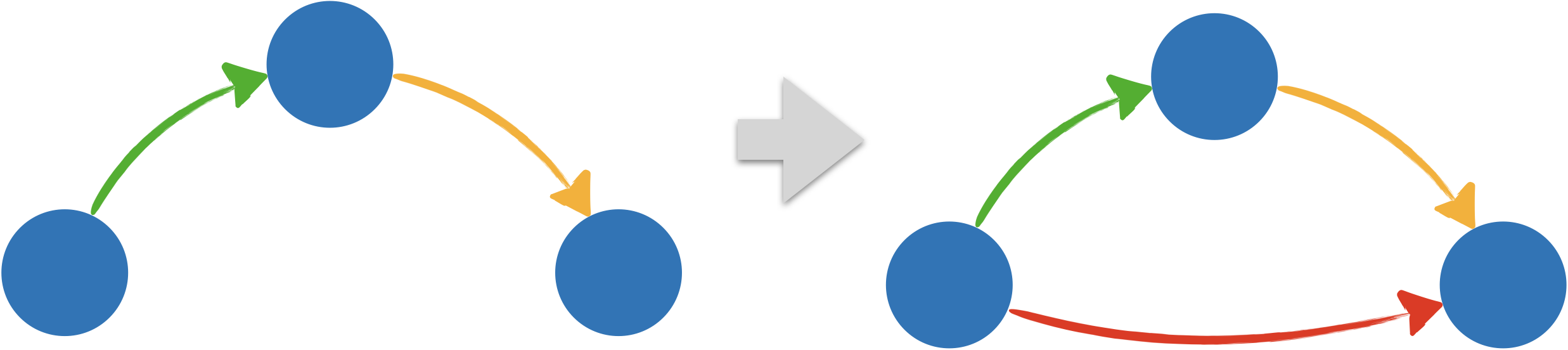
- $\mathcal{S}$ est transitif
- Pour toute formule $\phi$, $\mathcal{S}\Vdash^{\forall a, \forall \mathcal{V}}(\Box\phi\rightarrow \Box\Box\phi )$
- $(1)\Rightarrow(2)$
Soient $\mathcal{S}$ un système de transition transitif, $\mathcal{V}$ une valuation et $a$ un nœud.
Si $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Box\phi$ alors pour tout nœud $b$ tel que $a\longrightarrow b$, $\langle\mathcal{S},\mathcal{V},b\rangle\Vdash\phi$.
Pour montrer $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Box\Box\phi$, il suffit de montrer que pour tout $c$ tel qu'il existe $b$ vérifiant $a\longrightarrow b$ et $b\longrightarrow c$, on a $\langle\mathcal{S},\mathcal{V},c\rangle\Vdash\phi$.
Or puisque $\mathcal{S}$ est transitif, $a\longrightarrow b$ et $b\longrightarrow c$ impliquent $a\longrightarrow c$. D'où $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Box\phi$ entraîne $\langle\mathcal{S},\mathcal{V},c\rangle\Vdash\phi$. - $(2)\Rightarrow(1)$
Soit un système de transition non transitif $\mathcal{S}$ et soient $a$, $b$ et $c$ trois nœuds de $\mathcal{S}$ tels que $a\longrightarrow b$, $b\longrightarrow c$ et $a\not\!\!\longrightarrow c$. Soit $\mathcal{V}$ une valuation qui vérifie $d\in\mathcal{V}(P)$ si et seulement si $a\rightarrow d$.
Pour $\phi=P$, nous obtenons donc à la fois $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Box\phi$ et $\langle\mathcal{S},\mathcal{V},c\rangle\nVdash\phi$ ce qui montre que $\langle\mathcal{S},\mathcal{V},a\rangle\nVdash\Box\Box\phi$.
On note $\mathscr{C}_{tr.}$ la classe de tous les systèmes de transition transitifs.
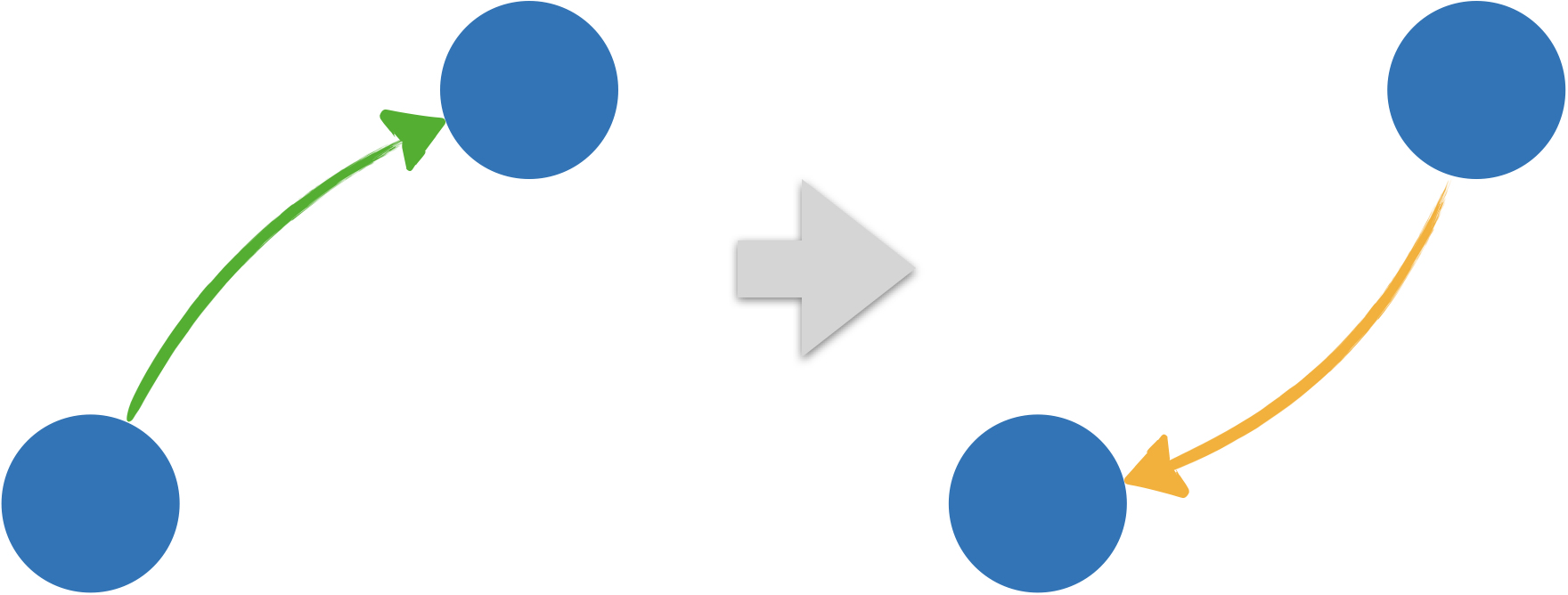
Pour tout système de transition $\mathcal{S}$, les affirmations suivantes sont équivalents :
- $\mathcal{S}$ est symétrique
- Pour toute formule $\phi$, $\mathcal{S}\Vdash^{\forall a, \forall \mathcal{V}}(\phi\rightarrow \Box\Diamond\phi)$
On peut traduire $\Box\Diamond\phi$ par “pour tout successeur possible, $\phi$ est vrai dans au moins un successeur”.
- $(1)\Rightarrow(2)$
Soient $\mathcal{S}$ un système de transition symétrique, $\mathcal{V}$ une valuation et $a$ un nœud.
On suppose $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash \phi$. Pour tout nœud $a$, soit $a$ n'a pas de successeur et la formule $\phi\rightarrow \Box\Diamond\phi$ est trivialement vérifiée (toute formule commençant par $\Box$ est vraie en un nœud sans successeur), soit $a$ possède un ou plusieurs successeurs et chacun d'entre eux possède alors $a$ comme successeur par symétrie du graphe. Tous ces nœuds ont donc au moins un successeur, $a$, où $\phi$ est vraie. Par conséquent, tous les successeurs de $a$ forcent $\Diamond \phi$. Et finalement, on a bien $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash \Box\Diamond\phi$. - $(2)\Rightarrow(1)$
S'il existe deux nœuds $a$ et $b$ tels que $a\longrightarrow b$ mais $b\,\,\not\!\!\longrightarrow a$, il suffit de considérer une valuation telle que $a\Vdash P$ et $c\Vdash\neg P$ pour tout nœud $c$ tel que $b\longrightarrow c$ pour obtenir $a\nVdash P \rightarrow\Box\Diamond P$.
On note $\mathscr{C}_{sym.}$ la classe de tous les systèmes de transition symétriques.
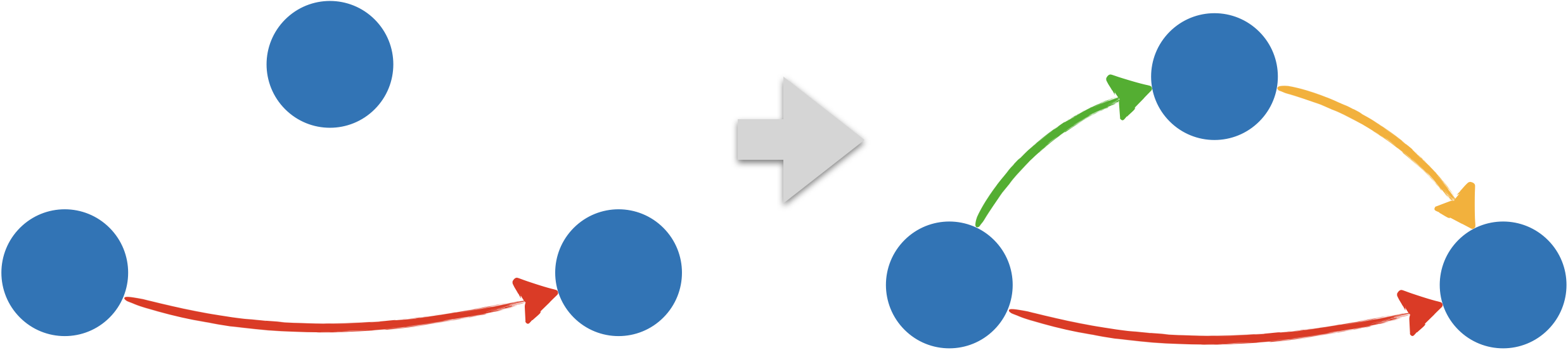
Pour tout système de transition $\mathcal{S}$, les affirmations suivantes sont équivalents :
- $\mathcal{S}$ est dense
- Pour toute formule $\phi$, $\mathcal{S}\Vdash^{\forall a, \forall \mathcal{V}}(\Box\Box\phi\rightarrow \Box\phi)$
- $(1)\Rightarrow(2)$
Soient $\mathcal{S}$ un système de transition dense, $\mathcal{V}$ une valuation et $a$ un nœud.
Supposons que $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Box\Box\phi$ est vérifié et montrons que $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Box\phi$ l'est également.
Soit $c$ un nœud vérifiant $a\longrightarrow c$. $\mathcal{S}$ étant dense, il existe $b$ tel que $a\longrightarrow b$ et $b\longrightarrow c$. Par conséquent, l'hypothèse $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Box\Box\phi$ entraîne aussitôt $\langle\mathcal{S},\mathcal{V},c\rangle\Vdash \phi$. - $(2)\Rightarrow(1)$
Soit un système de transition non dense $\mathcal{S}$ qui vérifie $\mathcal{S}\Vdash^{\forall a, \forall \mathcal{V}}(\Box\Box\phi\rightarrow \Box\phi)$ pour n'importe quelle formule $\phi$.
Si $\mathcal{S}$ n'est pas dense, il existe deux nœuds $a$ et $c$ tels que $a\longrightarrow c$ sans qu'aucun $b$ ne vérifie à la fois $a\longrightarrow b$ et $b\longrightarrow c$.
Considérons la valuation $\mathcal{V}$ définie par $d\in\mathcal{V}(P)$ si et seulement si $d\neq c$.
Il s'en suit que si $\langle\mathcal{S},\mathcal{V},c\rangle\nVdash P$ alors $\langle\mathcal{S},\mathcal{V},a\rangle\nVdash\Box P$, et pourtant $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Box\Box P$. D'où $\langle\mathcal{S},\mathcal{V},a\rangle\nVdash\Box\Box P \rightarrow \Box P$.
Pour tout système de transition $\mathcal{S}$, les affirmations suivantes sont équivalents :
- $\mathcal{S}$ est non borné à droite
- Pour toute formule $\phi$, $\mathcal{S}\Vdash^{\forall a, \forall \mathcal{V}}(\Box\phi\rightarrow \Diamond\phi)$

- $(1)\Rightarrow(2)$
Soient $\mathcal{S}$ un système de transition non borné à droite, $\mathcal{V}$ une valuation et $a$ un nœud.
On suppose que $a\Vdash\Box P$. La seule possibilité pour que $a\nVdash\Diamond P$, c'est que le nœud $a$ n'est aucun successeur or l'hypothèse que $\mathcal{S}$ est non broné à droite nous l'interdit, donc nécessairement $a\Vdash\Diamond P$. - $(2)\Rightarrow(1)$
Si un système de transition n'est pas borné à droite, il existe un nœud $a$ sans successeur. Supposons une valuation $\mathcal{V}$ telle que seul $a\in \mathcal{V}(P)$. On a alors $a\Vdash \Box P$ mais aussi $a\nvdash \Diamond P$.
On note $\mathscr{C}_{n.b.d.}$ la classe de tous les systèmes de transition non bornés à droite.
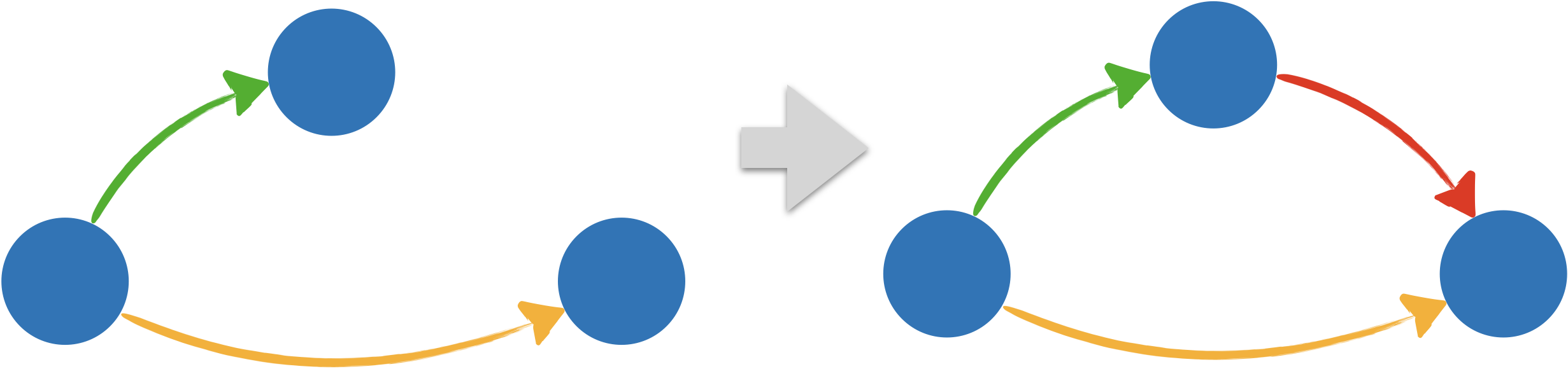
Pour tout système de transition $\mathcal{S}$, les affirmations suivantes sont équivalents :
- $\mathcal{S}$ est euclidien
- Pour toute formule $\phi$, $\mathcal{S}\Vdash^{\forall a, \forall \mathcal{V}}(\Diamond\phi\rightarrow \Box\Diamond\phi)$
- $(1)\Rightarrow(2)$
Soient $\mathcal{S}$ un système de transition euclidien, $\mathcal{V}$ une valuation et $a$ un nœud.
S'il existe un nœud $c$ tel que $a\longrightarrow c$ et $\langle\mathcal{S},\mathcal{V},c\rangle\Vdash \phi$, alors pour tout nœud $b$ tel que $a\longrightarrow b$, il existe un nœud $d$, tel que $b\longrightarrow d$ et $\langle\mathcal{S},\mathcal{V},d\rangle\Vdash \phi$. En effet, il suffit de prendre $d=c$ puisque le caractère euclidien du graphe assure que de $a\longrightarrow b$ et $a\longrightarrow c$, nous obtenons $b\longrightarrow c$. - $(2)\Rightarrow(1)$
Si un système de transition n'est pas euclidien, il existe des nœuds $a$, $b$, $c$, avec $a\longrightarrow b$ et $a\longrightarrow c$, mais sans arc $b\longrightarrow c$, alors il suffit de considérer une valuation telle que $\langle\mathcal{S},\mathcal{V},c\rangle\Vdash P$ et pour tout nœud $d\neq c$, $\langle\mathcal{S},\mathcal{V},d\rangle\nVdash P$. On obtient ainsi $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash \Diamond P$, mais comme il n'y a pas d'arc de $b$ vers $c$, $\langle\mathcal{S},\mathcal{V},b\rangle\nVdash \Diamond P$ et par conséquent $\langle\mathcal{S},\mathcal{V},a\rangle\nVdash \Box\Diamond P$.
Soit $\Gamma$ un ensemble de formules. On écrit :
-
$\mathcal{S}\Vdash^{\forall a, \forall\mathcal{V}} \Gamma$ si et seulement si pour toute formule $\phi\in\Gamma$, $\mathcal{S}\Vdash^{\forall a, \forall\mathcal{V}} \phi$
$\mathcal{S}$ est un système de transition tel qu’en tout nœud et quelle que soit la valuation considérée, il satisfait tout ce que “raconte” $\Gamma$. C’est donc par sa seule forme que ce système de transition vérifie l’ensemble des formules de $\Gamma$. -
$\mathscr{C} \Vdash\Gamma$ si et seulement si pour toute formule $\phi\in\Gamma$, $\mathscr{C}\Vdash \phi$
Même affirmation que la précédente mais pour une classe de systèmes de transition toute entière plutôt que pour un seul représentant. En ce sens, la plus grande classe $\mathscr{C}$ qui vérifie $\mathscr{C}\Vdash\Gamma$ octroie une sorte de caractérisation par la seule forme des graphes de ce que raconte $\Gamma$.
Conséquences sémantiques
Soient $\Gamma$ un ensemble de formules et $\mathscr{C}$ une classe de systèmes de transition.
$\phi$ est une conséquence sémantique globale de $\Gamma$ (noté $\Gamma\models^{\forall a}_\mathscr{C}\phi$) si et seulement si pour tout système de transition $\mathcal{S}\in \mathscr{C}$, et toute valuation $\mathcal{V}$, si $\langle\mathcal{S},\mathcal{V}\rangle\Vdash^{\forall a}\Gamma$ alors $\langle\mathcal{S},\mathcal{V}\rangle\Vdash^{\forall a}\phi$
Plus simplement, une formule est conséquence d’un ensemble d’hypothèses si chaque fois que ces hypothèses sont vraies dans un modèle de la classe considérée, alors cette formule est également vraie dans ce modèle.
Soient $\Gamma$ un ensemble de formules et $\mathscr{C}$ une classe de systèmes de transition.
$\phi$ est une conséquence sémantique locale de $\Gamma$ (noté $\Gamma\models_\mathscr{C}\phi$) si et seulement si pour tout système de transition $\mathcal{S}\in \mathscr{C}$, toute valuation $\mathcal{V}$, et tout nœud $a\in N$, si $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Gamma$ alors $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\phi$
La conséquence sémantique locale est plus forte que la globale au sens où si $\Gamma\models_\mathscr{C}\phi$ alors $\Gamma\models^{\forall a}_\mathscr{C}\phi$. L’inverse est généralement faux comme le montre l’exemple suivant :
Soient $\mathscr{C}$ la classe de tous les systèmes de transition, $\Gamma=\set{P}$ et $\phi=\Box P$.
On a $\Gamma\models^{\forall a}_\mathscr{C}\phi$.
En effet, considérons un modèle quelconque $\langle\mathcal{S},\mathcal{V}\rangle$ qui vérifie $\langle\mathcal{S},\mathcal{V}\rangle\Vdash^{\forall a}\Gamma$, ce qui revient ici à affirmer que $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash P$ est vraie pour tout nœud $a$. En particulier, pour tout nœud $b$ tel que $a\longrightarrow b$, la relation $\langle\mathcal{S},\mathcal{V},b\rangle\Vdash P$ est vérifiée, ce qui signifie que tout nœud $a$ vérifie $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash \Box P$.
Par contre, il est facile de trouver un modèle où $\Gamma\models_\mathscr{C}\phi$ est faux :

Plus prosaïquement, la conséquence locale dit que partout où il y a $\Gamma$, il y a $\phi$, alors que la conséquence globale dit que s’il y a $\Gamma$ partout alors il y a $\phi$ partout.
Il existe un lien entre les deux conséquences sémantiques :
$\Gamma\models^{\forall a}_\mathscr{C}\phi$ si et seulement si $\set{\Box^n\psi|n\in\mathbb{N},\psi\in\Gamma}\models_\mathscr{C}\phi$ (où $\Box^n\psi = \underbrace{\Box\Box\ldots\Box}_{n}\psi$ si $n>0$ et $\psi$ si $n =0$)
$\Box^n$ permet en quelque sorte de généraliser la vérité d’un nœud puisque dire qu’on a $\Box^n\psi$ en $a$ implique que $\psi$ est vraie en tout nœud atteignable depuis $a$.
- $\Leftarrow$
Si on a $\Gamma$ en tout nœud, alors en un nœud $a$ quelconque, on a nécessairement $\Box^n\psi$ vraie pour tout $n$ et tout $\psi$ dans $\Gamma$. Or par hypothèse, cela implique que $\phi$ est vraie en ce nœud. Et comme la raisonnement ne dépend pas du nœud $a$, cela montre que $\phi$ est vraie en tout nœud. - $\Rightarrow$
Démontrons la contraposée : si $\set{\Box^n\psi|n\in\mathbb{N},\psi\in\Gamma}\not\models_\mathscr{C}\phi$ alors $\Gamma\not\models^{\forall a}_\mathscr{C}\phi$.
Soient $\mathcal{S}=(N,A)$ un système de transition, $\mathcal{V}$ une valuation et $a\in N$ un nœud, tels que $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\set{\Box^n\psi|n\in\mathbb{N},\psi\in\Gamma}$ alors que $\langle\mathcal{S},\mathcal{V},a\rangle\nVdash\phi$.
Fabriquons le système de transition $\mathcal{T}=(N',A')$ qui correspond à la restriction de $\mathcal{S}$ à l'ensemble des nœuds accessibles depuis $a$ et munissons-le d'une valuation $\mathcal{V}'$ identique à $\mathcal{V}$ pour ces nœuds.
Par construction, dans le modèle $\langle\mathcal{T},\mathcal{V}'\rangle$ ainsi formé, $\psi$ est vraie en tout nœud : $\langle\mathcal{T},\mathcal{V}'\rangle\Vdash^{\forall a}\psi$. Cela entraîne que $\langle\mathcal{T},\mathcal{V}'\rangle\Vdash^{\forall a}\Gamma$, et pourtant $\langle\mathcal{T},\mathcal{V}',a\rangle\nVdash\phi$ par hypothèse, ce qui implique $\Gamma\not\models^{\forall a}_\mathscr{C}\phi$.
Si $\mathscr{C}_\phi$ et $\mathscr{C}_\psi$ désignent respectivement tous les systèmes dans lesquels $\phi$ est vraie et tous ceux où $\psi$ est vraie, alors $\phi\models^{\forall a}_\mathscr{C}\psi$ est équivalent à l’inclusion $\mathscr{C}_\phi\subseteq\mathscr{C}_\psi$.
Donc si on a à la fois $\phi\models^{\forall a}_\mathscr{C}\psi$ et $\psi\models^{\forall a}_\mathscr{C}\phi$, alors $\mathscr{C}_\phi = \mathscr{C}_\psi$.
Théories, équivalence et bisimulation
On appelle théorie du modèle $\langle\mathcal{S},\mathcal{V}\rangle$ l’ensemble de toutes les formules qui sont vraies dans ce modèle : $$Th_\mathcal{M}=\set{\phi|\langle\mathcal{S},\mathcal{V}\rangle\Vdash^{\forall a}\phi}$$
La théorie d’un modèle est composée de toutes les formules décrivant ce modèle.
Deux modèles sont distinguables par la logique modale s’ils n’ont pas la même théorie.
On appelle théorie locale d’un modèle $\langle\mathcal{S},\mathcal{V}\rangle$ au nœud $a$ l’ensemble de toutes les formules qui sont vraies dans ce modèle : $$Th_{(\mathcal{M},a)}=\set{\phi|\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\phi}$$
Soient $\mathcal{M}$ et $\mathcal{N}$ deux modèles de la logique modale.
- $\mathcal{M}$ et $\mathcal{N}$ sont équivalents s'ils ont la même théorie :
$\mathcal{M} \equiv \mathcal{N}$ si et seulement si $Th_\mathcal{M}=Th_\mathcal{N}$ - $\mathcal{M}$ et $\mathcal{N}$ sont localement équivalents s'ils partagent la même théorie locale :
$(\mathcal{M},a) \equiv (\mathcal{N},b)$ si et seulement si $Th_{(\mathcal{M},a)}=Th_{(\mathcal{N},b)}$
Les deux modèles suivants sont équivalents ($\mathcal{M} \equiv \mathcal{N}$).
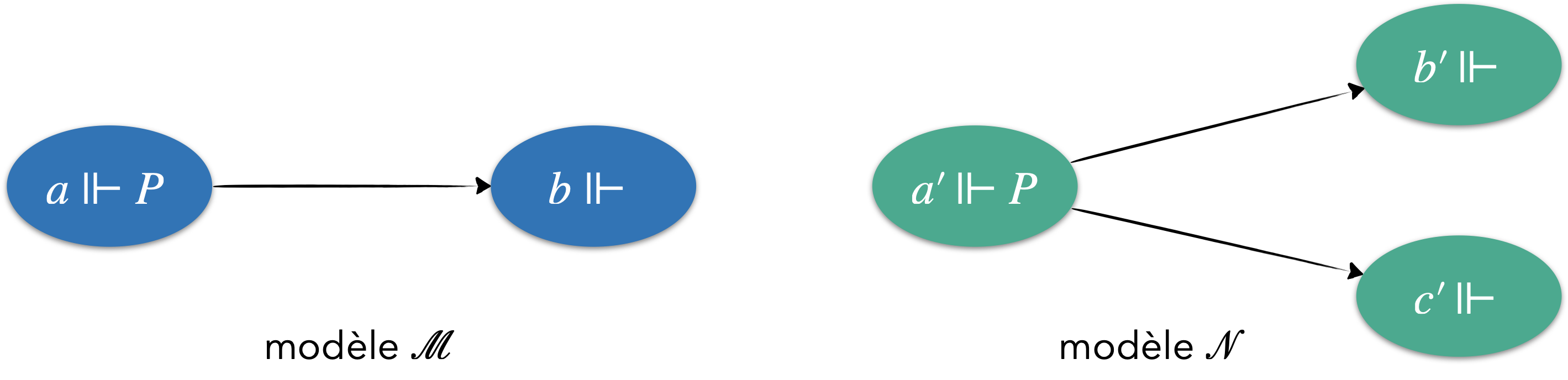
La bisimulation va nous permettre de reconnaître que ces modèles sont localement équivalents.
Deux modèles correspondent en quelque sorte à deux univers parallèles. Mais il se peut que depuis un des mondes du premier univers, tout paraisse exactement identique à ce que l’on perçoit depuis un monde du deuxième univers. Bien que les univers soient différents, ses “habitants” ne peuvent pas les différentier. On dit qu’ils sont indiscernables ou bisimilaires. Deux mondes sont indiscernables s’il n’existe pas de formule vraie dans l’un et fausse dans l’autre.
Un jeu à deux joueurs à information parfaite, le jeu de bisimulation, est défini de telle sorte que le joueur appelé Duplicateur possède une stratégie gagnante si et seulement si les deux mondes (associés à leurs modèles respectifs) qui interviennent dans le jeu sont indiscernables.
Plus besoin de passer en revue toutes les formules possibles pour déterminer si deux mondes sont ou non discernables…
Soient $\mathcal{M}=\langle\mathcal{S}=(N,A) , \mathcal{V}\rangle$ et $\mathcal{N}=\langle\mathcal{T}=(M,B),\mathcal{W}\rangle$ deux modèles de la logique modale et soient $a\in N$ et $b\in M$ deux nœuds.
Le jeu de bisimulation $\mathbb{Bis}((\mathcal{M},a),(\mathcal{N},b))$ est défini comme suit :
- il comprend deux joueurs appelés Duplicateur et Corrupteur.
Le Duplicateur ($\text{D}_{up}$) cherche à montrer que les deux modèles sont localement bisimilaires, alors que le Corrupteur ($\text{C}_{or}$) au contraire veut montrer qu'ils ne le sont pas.
Un coup, pour chacun des joueurs, consiste à choisir un nœud dans un système de transition. Les nœuds de départ étant $a$ dans $\mathcal{S}$ et $b$ dans $\mathcal{T}$. - À chaque tour, pour une position $a'$ dans $\mathcal{M}$ et une position $b'$ dans $\mathcal{N}$, $\text{C}_{or}$ choisit d'abord de jouer dans $\mathcal{S}$ ou dans $\mathcal{T}$ puis il choisit un arc permettant d'arriver à un successeur du nœud $a'$ ou $b'$ et $\text{D}_{up}$ répond en choisissant un successeur dans l'autre modèle tel que les nœuds choisit dans chaque modèle satisfont les mêmes variables propositionnelles.
- Fin de la partie :
- S'il existe une variable $P$ telle que la position initiale vérifie $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash P$ si et seulement si $\langle\mathcal{T},\mathcal{W},b\rangle\nVdash P$, alors $\text{C}_{or}$ l'emporte.
- Si un joueur ne peut plus avancer alors il perd la partie.
- Si la partie est infinie, $\text{D}_{up}$ l'emporte.
Exemple 1 :
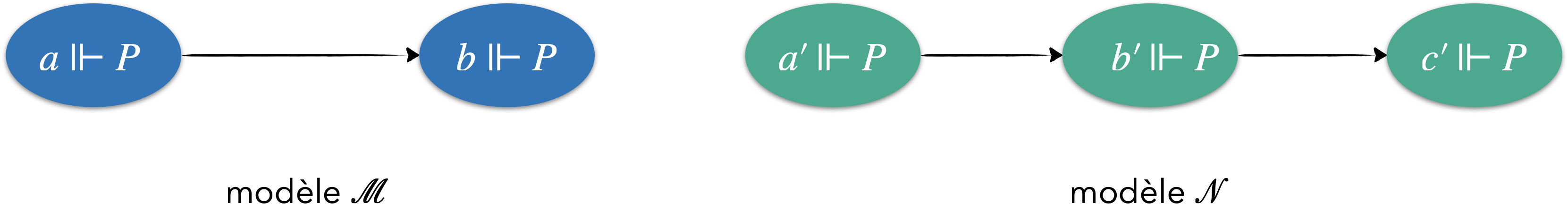
- $\text{C}_{or}$ choisit de joueur dans $\mathcal{N}$ puis va en $b'$.
- $\text{D}_{up}$ n'a pas d'autre choix que d'aller en $b$.
- $\text{C}_{or}$ choisit à nouveau de joueur dans $\mathcal{N}$ et va en $c'$.
- $\text{D}_{up}$ perd car il ne peut plus avancer.
Exemple 2 :
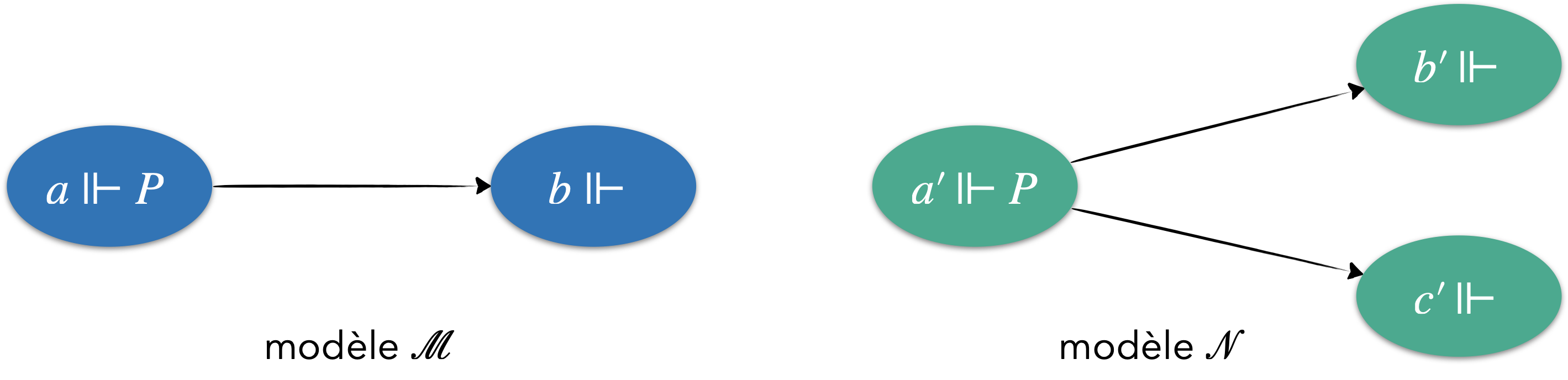
- Si $\text{C}_{or}$ choisit d'aller en $b'$ ou en $c'$, $\text{D}_{up}$ va en $b$ (il n'a pas trop le choix en même temps...).
- Si $\text{C}_{or}$ choisit d'aller en $b$, $\text{D}_{up}$ va en $b'$ ou en $c'$ (c'est sans importance).
Exemple 3 :
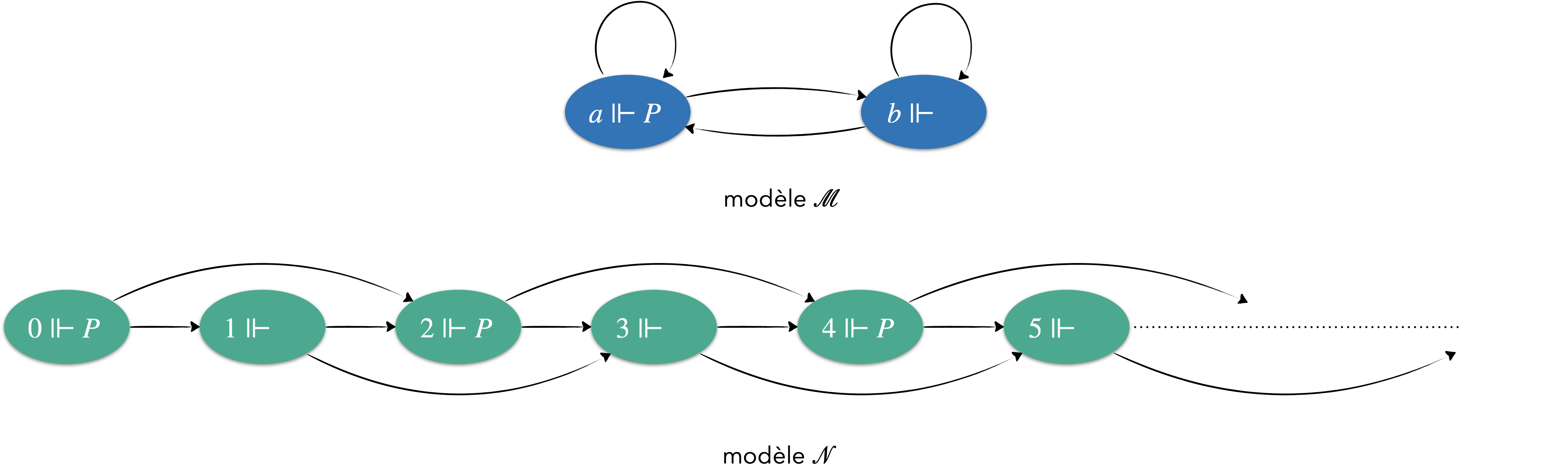
- l'ensemble des nœuds est $\mathbb{N}$,
- de tout nœud $n\in\mathbb{N}$ part deux arcs : $n\longrightarrow n+1$ et $n\longrightarrow n+2$
- $2n\Vdash P$ et $2n+1\nVdash P$
- si $\text{C}_{or}$ joue dans $\mathcal{N}$ et va sur $n$, à aller sur $a$ si $n$ est pair et sur $b$ sinon,
- si $\text{C}_{or}$ joue dans $\mathcal{M}$ et va sur $a$, à aller sur $n+2$ si $n$ est pair et sur $n+1$ sinon,
- si $\text{C}_{or}$ joue dans $\mathcal{M}$ et va sur $b$, à aller sur $n+1$ si $n$ est pair et sur $n+2$ sinon,
Théorème de Henessy-Milner : $(\mathcal{M},a)\equiv(\mathcal{N},b)$ si et seulement si $\text{D}_{up}$ a une stratégie gagnante dans $\mathbb{Bis}((\mathcal{M},a),(\mathcal{N},b))$.