
Notes de lecture du livre La logique pas à pas de Jacques Duparc que je paraphrase allégrement.
Calcul des propositions
Sémantique
Modèle
La sémantique concerne l’interprétation des formules. Le calcul propositionnel est très frustre à cet égard. Une variable propositionnelle vaut soit 1, soit 0, c’est-à-dire qu’elle est soit vraie, soit fausse. Et il en est de même pour une formule dont l’interprétation se déduit de celles des variables et des règles qu’impliquent les connecteurs.
À partir de l’ensemble des variables $VAR$, on peut construire une fonction $\delta$ qui associe une valeur de vérité à certains éléments de $VAR$ :
$\delta :\;VAR\rightarrow\set{0,1}$
$\delta$ est une distribution de valeurs de vérité.
$\delta$ permet de définir un modèle $\mathcal{M}$ du calcul propositionnel.
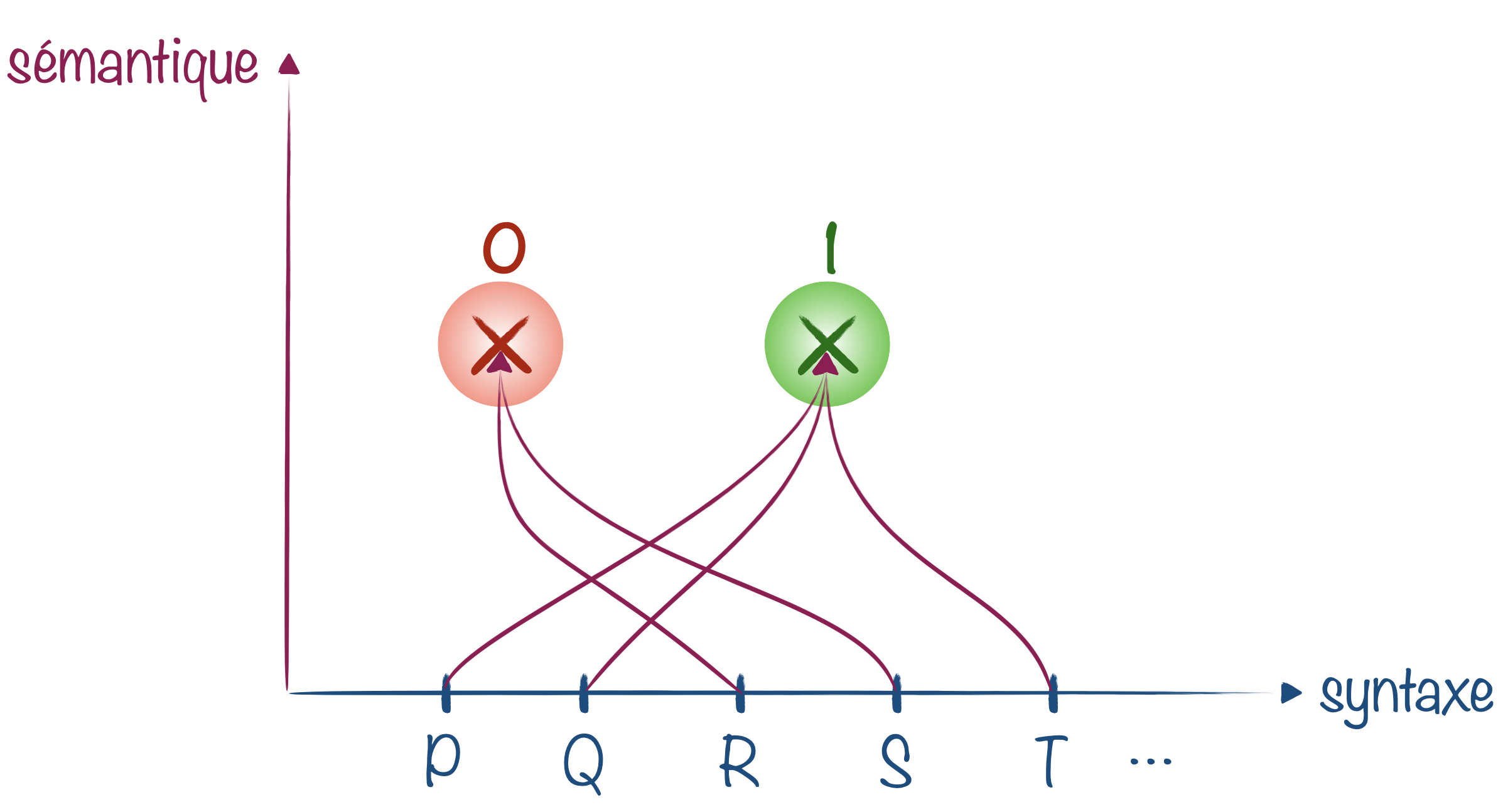
Imaginons qu’un ensemble de formules ne possèdent que deux variables $P$ et $Q$. On a alors 4 modèles différents possibles :
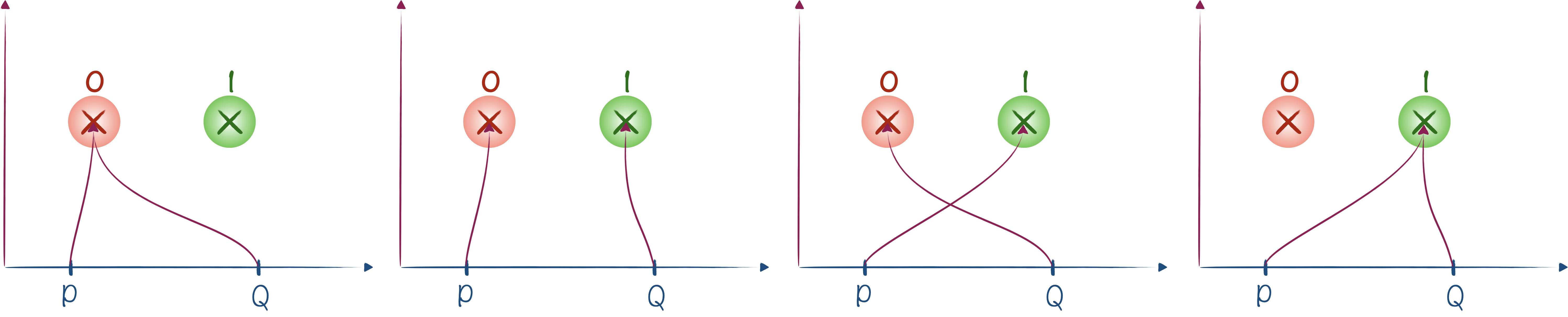
- $\mathcal{M}_1$ pour lequel la distribution de valeur de vérité $\delta_1$ est définie par : $\delta_1(P) = 0$ et $\delta_1(Q)=0$
- $\mathcal{M}_2$ pour lequel la distribution de valeur de vérité $\delta_2$ est définie par : $\delta_2(P) = 0$ et $\delta_2(Q)=1$
- $\mathcal{M}_3$ pour lequel la distribution de valeur de vérité $\delta_3$ est définie par : $\delta_3(P) = 1$ et $\delta_3(Q)=0$
- $\mathcal{M}_4$ pour lequel la distribution de valeur de vérité $\delta_4$ est définie par : $\delta_4(P) = 1$ et $\delta_4(Q)=1$
Pour un modèle $\mathcal{M}$, si $\delta(P)=1$, on note $\mathcal{M}\models P$. Cela signifie que $P$ est vraie dans le modèle $\mathcal{M}$.
À linverse, si $\delta(P)=0$, on écrira $\mathcal{M}\not\models P$.
Si $\mathcal{M}\not\models P$ alors $\mathcal{M}\models \neg P$.
Exemple :
si $\mathcal{M}\models P,\neg Q,R$, cela signifie que dans le modèle $\mathcal{M}$, $P$ et $R$ sont vraies, mais $Q$ est fausse.
Évaluation des formules
Pour évaluer des formules, il faut pouvoir étendre la fonction de distribution de valeurs de vérité des seules variables propositionnelles à toutes les formules de $\mathcal{F}$. $\delta$ devient alors $\delta_\mathcal{F}$ et on construit $\delta_\mathcal{F}$ à partir de $\delta$ en utilisant les règles suivantes :
- $\delta_\mathcal{F}(\phi) = \delta(\phi)$ si $\phi$ est une variable propositionnelle.
- $\delta_\mathcal{F}(\neg\phi) = 1- \delta_\mathcal{F}(\phi)$ (non $\phi$ est vraie seulement si $\phi$ est fausse).
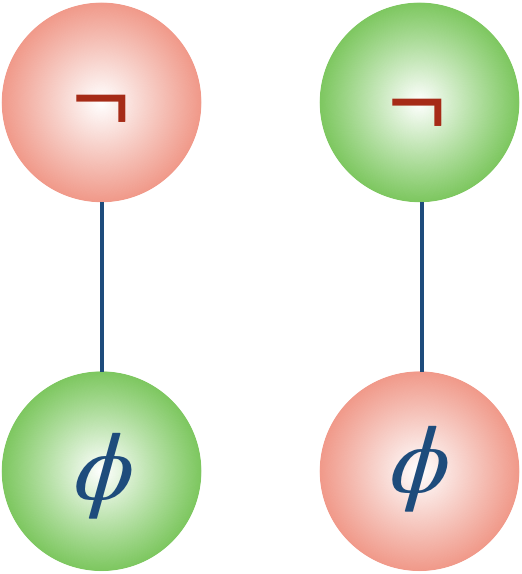
- $\delta_\mathcal{F}(\phi \lor\psi) = \max(\delta_\mathcal{F}(\phi) ,\delta_\mathcal{F}(\psi) ) $ ($\phi \lor\psi$ est toujours vraie sauf lorsque les deux sous-formules $\phi$ et $\psi$ sont toutes deux fausses).

- $\delta_\mathcal{F}(\phi \land \psi) = \delta_\mathcal{F}(\phi) \cdot \delta_\mathcal{F}(\psi)$ ($\phi \land\psi$ est toujours fausse sauf lorsque les deux sous-formules $\phi$ et $\psi$ sont toutes deux vraies).

- $\delta_\mathcal{F}(\phi \rightarrow \psi) = \max(1- \delta_\mathcal{F}(\phi) ,\delta_\mathcal{F}(\psi) )$ ($\phi \rightarrow \psi$ est toujours vraie sauf quand à la fois $\phi$ est vraie et $\psi$ est fausse).

- $\delta_\mathcal{F}(\phi \leftrightarrow \psi) = \max(\delta_\mathcal{F}(\phi) \cdot\delta_\mathcal{F}(\psi), (1-\delta_\mathcal{F}(\phi) )\cdot(1-\delta_\mathcal{F}(\psi) ) )$ ($\phi \leftrightarrow \psi$ est vraie lorsque $\phi$ et $\psi$ ont la même valeur de vérité).

Avec nos petits coloriages, on peut maintenant s’atteler à la valeur de vérité d’une formule complexe dans un modèle donné.
Soit le modèle $\mathcal{M}$ défini par $\mathcal{M}\models P,\neg Q, R$ et la formule $\phi$ qu’on s’est amusé à linéariser à la fin du chapitre sur la syntaxe. On va partir des feuilles et remonter jusqu’à la racine de l’arbre.
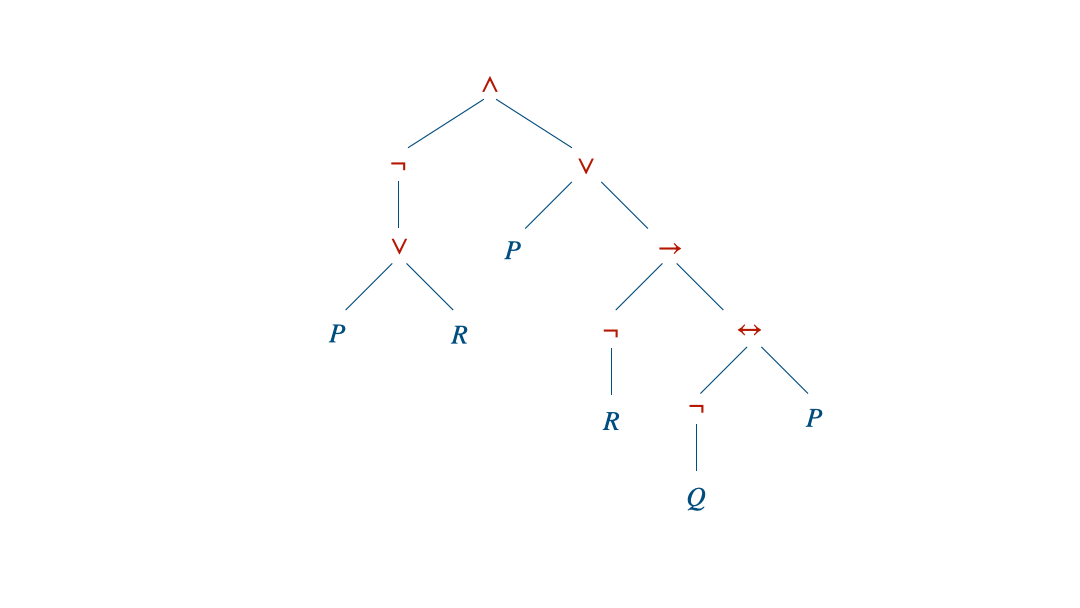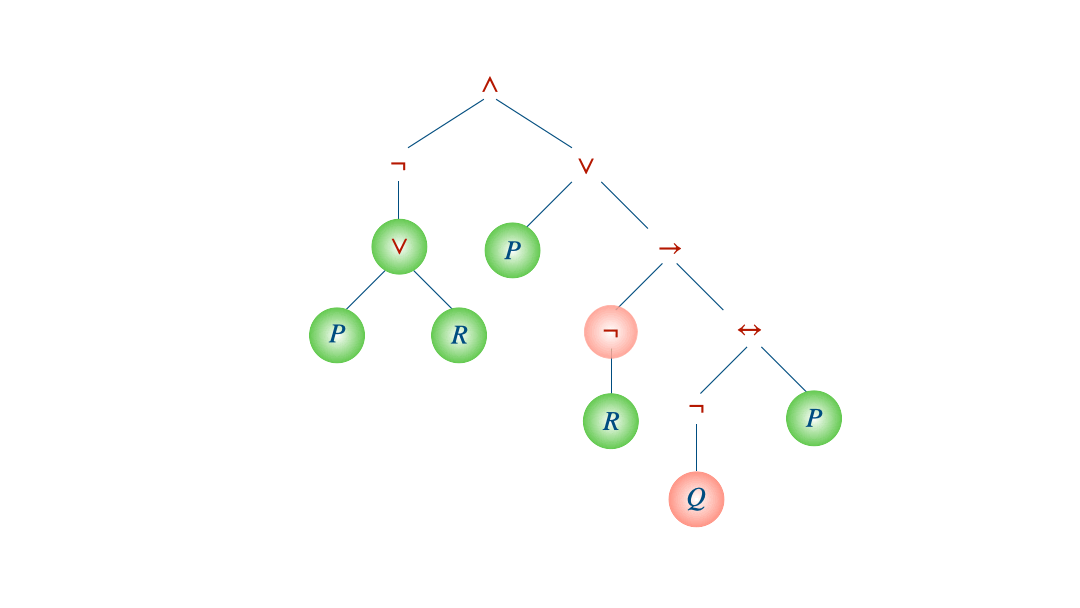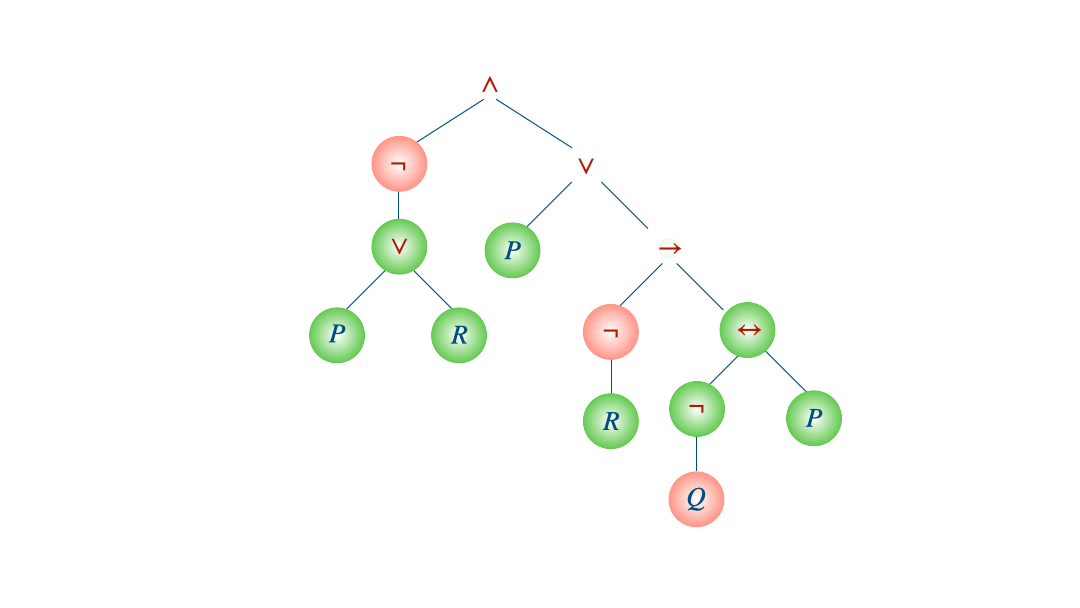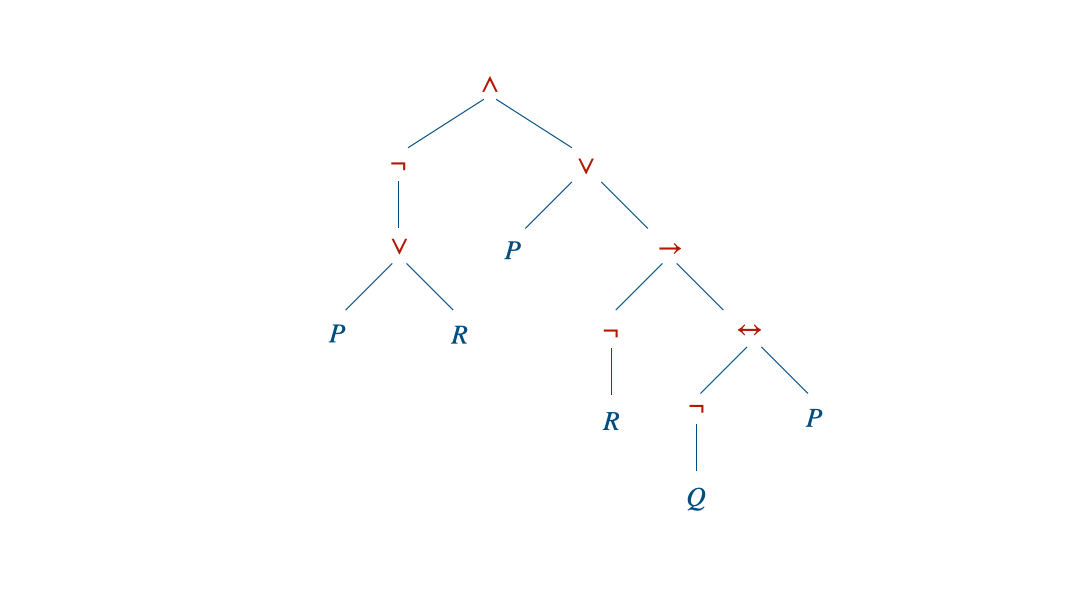
Comme la racine est fausse, la formule $\phi$ est fausse dans ce modèle : $\mathcal{M}\not\models\phi$.
La formule n’est d’ailleurs vraie que dans un seul des 8 modèles possibles.
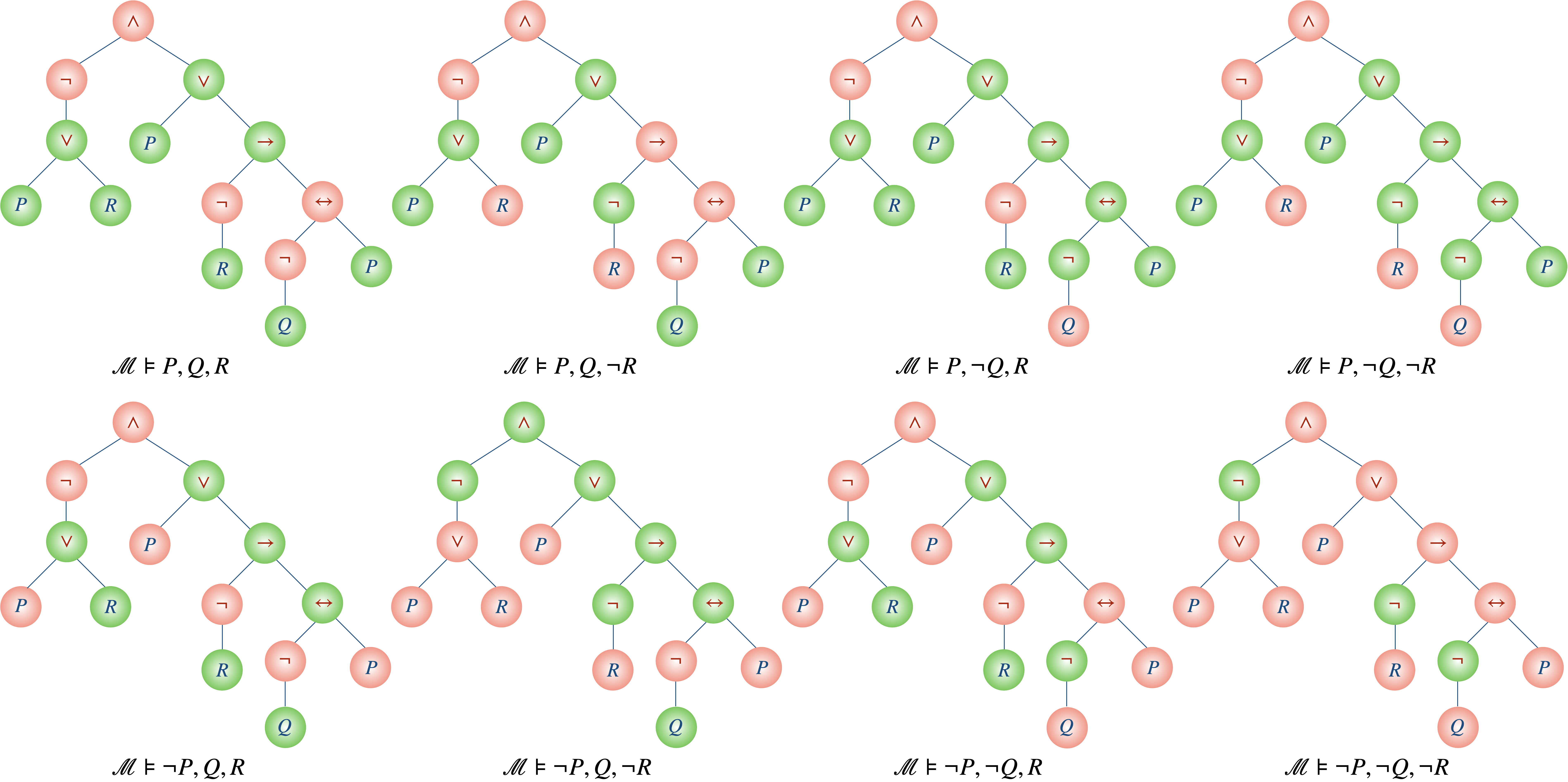
Si la hauteur $n$ de la formule est grande, le coloriage devient vite impraticable car trop long. En imaginant que tous les opérateurs sont binaires et que chaque branche est de longueur $n$, cela nous demanderait le coloriage de $0+2+2^2+\ldots+2^{n-1}=2^n-1$ nouveaux nœuds. Avec une formule de hauteur 31, ce qui ne semble pas délirant, on pourrait se retrouver à devoir colorier plus d’un milliard de nœuds…
Formules logiquement équivalentes
Une formule $\phi$ est satisfaite dans un modèle $\mathcal{M}$ si elle est vraie dans ce modèle. La distribution de valeur de vérité $\delta$ qui caractérise $\mathcal{M}$ vaut alors 1.
$\mathcal{M}\models\phi$ signifie que $\delta_\mathcal{F}(\phi) = 1$ et $\mathcal{M}\not\models\phi$ signifie que $\delta_\mathcal{F}(\phi) = 0$.
Deux formules $\phi$ et $\psi$ sont deux formules équivalentes ($\phi\equiv\psi$) ssi elles sont satisfaites dans les mêmes modèles (mêmes valeurs de vérité dans les mêmes modèles).
$\equiv$ est une équivalence sémantique alors que $\leftrightarrow$ est une équivalence syntaxique, parfois appelée équivalence matérielle.
$\phi\equiv\psi$ ssi (pour tout modèle $\mathcal{M}$, $\mathcal{M}\models \phi\leftrightarrow \psi$).
Preuve :
- Si les deux formules sont équivalentes dans un modèle, alors $\delta_\mathcal{F}(\phi)=\delta_\mathcal{F}(\psi)$ dans ce modèle. Et par conséquent $\delta_\mathcal{F}(\phi\leftrightarrow\psi)=1$.
- Inversement, si la formule $\phi\leftrightarrow\psi$ est vraie dans tout modèle, les valeurs que prennent $\phi$ et $\psi$ dans ces modèles sont les mêmes.
La relation est :
- réflexive : $\phi\equiv\phi$
- symétrique : $\phi\equiv\psi$ ssi $\psi\equiv\phi$
- transitive : Si ($\phi\equiv\psi$ et $\psi \equiv\theta$) alors $\psi\equiv\theta$
Donc il s'agit bien d'une relation d'équivalence.
Théorie et conséquence sémantique
Une théorie $\mathcal{T}$ du calcul des propositions est un ensemble de formules : $\mathcal{T} \sube \mathcal{F}$.
- $\mathcal{T}$ est satisfaite dans le modèle $\mathcal{M}$ ($\mathcal{M}$ est un modèle de $\mathcal{T}$), noté $\mathcal{M}\models\mathcal{T}$, si pour toute formule $\phi$ de $\mathcal{T}$, $\mathcal{M}\models\phi$.
- $\mathcal{T}$ est satisfaisable ou consistante s'il existe au moins un modèle $\mathcal{M}$ tel que $\mathcal{M}\models\mathcal{T}$.
- $\mathcal{T}$ est inconsistante si $\mathcal{T}$ n'est pas satisfaisable.
Une théorie est inconsistante lorsqu’elle se contredit. Elle dit alors quelque chose et son contraire, ce qui ne peut être vérifié dans aucun modèle.
Comparons maintenant deux théories $\mathcal{T}$ et $\mathcal{T’}$ :
- $\mathcal{T'}$ est une conséquence sémantique de $\mathcal{T}$, noté $\mathcal{T} \models \mathcal{T'}$ si tout modèle satisfaisant $\mathcal{T}$ satisfait aussi $\mathcal{T'}$.
- $\mathcal{T}$ et $\mathcal{T'}$ sont deux théories équivalentes, noté $\mathcal{T} \equiv \mathcal{T'}$, si elles ont exactement les mêmes modèles.
Plus une théorie raconte de choses, moins elle possède de modèles. Et si elle raconte trop de choses, elle finit par devenir inconsistante car plus aucun modèle ne peut la satisfaire.
On écrit $\mathcal{T}\models\phi$ si la théorie $\mathcal{T’}$ se réduit au singleton $\set{\phi}$.
Et $\models\phi$ est un raccourci pour $\empty \models \phi$ ce qui signifie que $\phi$ est une conséquence logique de la théorie vide. Or la théorie vide ne dit rien et est donc satisfaite dans tous les modèles. Cela revient donc à dire que $\phi$ est vraie dans tous les modèles. $\phi$ est appelée une tautologie.
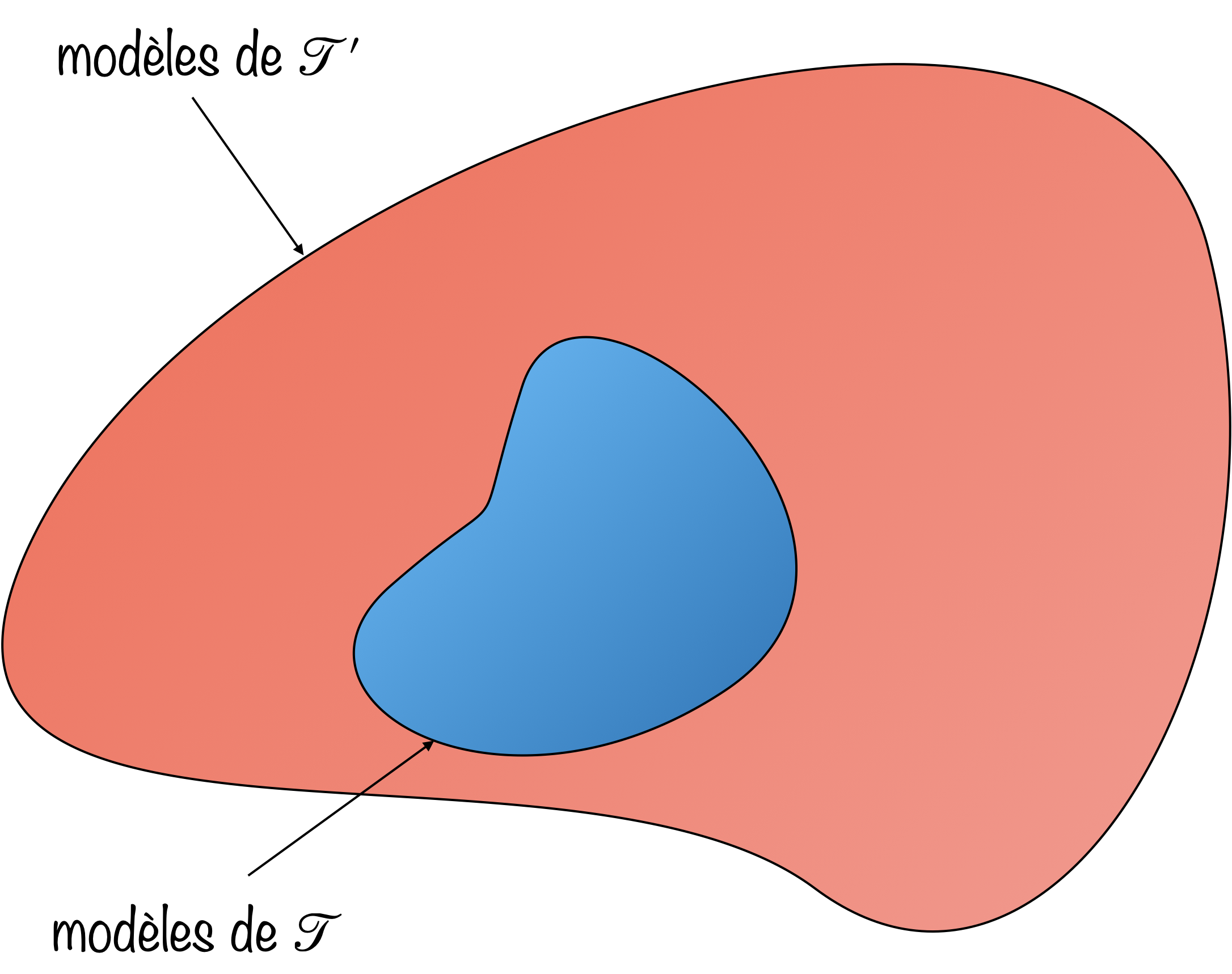
$\mathcal{T}\models\mathcal{T’}$ ssi l’ensemble des modèles de $\mathcal{T}$ est contenu dans l’ensemble des modèles de $\mathcal{T’}$.
En effet, $\mathcal{T’}$ est une conséquence sémantique de $\mathcal{T}$ si elle est vraie partout où $\mathcal{T}$ est vraie.
Deux théories équivalentes ont exactement les mêmes modèles ($\mathcal{T}\equiv \mathcal{T’}$ correspond à avoir à la fois $\mathcal{T}\models \mathcal{T’}$ et $\mathcal{T’}\models \mathcal{T}$), ce qui revient à dire qu’il n’existe pas de modèle pouvant les discriminer. Elles ne sont pas nécessairement égales (pas nécessairement le même ensemble de formules), mais elles sont égales sur le plan sémantique puisqu’elles signifient la même chose.
La notion de conséquence sémantique est la version sémantique de la notion de déduction. Dire qu’une formule est une conséquence sémantique d’une théorie, c’est affirmer que partout où la théorie est satisfaite (c.-à-d. quand les hypothèses sont vraies), la formule l’est également. La formule découle donc de la théorie.
- Si $\mathcal{T}$ est satisfaisable et $\mathcal{T'}\sube\mathcal{T}$, alors $\mathcal{T'}$ est également satisfaisable.
En restreignant une théorie, on conserve la non contradiction.
Le contraire n'est évidemment pas vrai. Si on étend une théorie (en ajoutant de nouvelles formules), on diminue le nombre de modèles qui la satisfait. Et on accroît ce nombre de modèles en enlevant des formules à la théorie, pour atteindre à la limite tous les modèles possibles lorsque la théorie devient vide. - Si $\mathcal{T'}$ est inconsistante et $\mathcal{T'}\sube\mathcal{T}$, alors $\mathcal{T}$ est également inconsistante.
Étendre une théorie inconsistante ne peut pas la rendre satisfaisable. - Si $\mathcal{T'}\models\phi$ et $\mathcal{T'}\sube\mathcal{T}$, alors $\mathcal{T}\models\phi$. Si $\phi$ est la conséquence d'une théorie, alors elle est la conséquence de toute théorie qui étend celle-ci (puisque le nombre de modèles satisfaisant cette théorie étendue s'est réduit et qu'on ne peut donc pas y trouver un nouveau modèle où $\phi$ deviendrait fausse).
- $\mathcal{T}$ est inconsistante ssi $\mathcal{T}\models\phi\land\neg\phi$.
- $\mathcal{T}$ est inconsistante ssi pour toute formule $\phi$, $\mathcal{T}\models\phi$. En effet, la plus grande théorie possible ($\mathcal{F}$) contient toute formule $\phi$ et sa négation.
- $\mathcal{T}\models\phi$ ssi $\mathcal{T}\cup\set{\neg\phi}$ est inconsistante.
En effet, dire que $\phi$ est conséquence sémantique de $\mathcal{T}$, c'est dire que $\phi$ est vraie dans tous les modèles de $\mathcal{T}$ et donc que $\neg\phi$ est fausse dans tous les modèles de $\mathcal{T}$. Impossible donc pour un modèle de satisfaire à la fois $\mathcal{T}$ et $\neg\phi$.
À l'inverse, si $\mathcal{T}\cup\set{\neg\phi}$ est inconsistante, alors $\neg\phi$ est fausse dans tous les modèles de $\mathcal{T}$ et donc $\phi$ est vraie dans tous les modèles de $\mathcal{T}$. D'où $\mathcal{T}\models\phi$. - $\mathcal{T}\cup\set{\phi}\models\psi$ ssi $\mathcal{T}\models\phi\rightarrow\psi$.
La seule possibilité pour que $\phi\rightarrow\psi$ soit fausse est si à la fois $\phi$ est vraie et $\psi$ est fausse. Or si $\mathcal{T}\cup\set{\phi}\models\psi$, cela signifie que si $\phi$ est vraie dans un modèle, alors $\psi$ est nécessairement vraie dans ce même modèle.
À l'inverse, si $\phi\rightarrow\psi$ est conséquence de $\mathcal{T}$, alors $\psi$ est vraie dans tous les modèles de $\mathcal{T}\cup\set{\phi}$ puisque $\phi\rightarrow\psi$ est vraie dans tous les modèles de $\mathcal{T}$.
En d'autres termes, déduire $\phi\rightarrow\psi$ de nos hypothèses $\mathcal{T}$, c'est la même chose que déduire $\psi$ en faisant l'hypothèse supplémentaire qu'on a $\phi$.
Substitution de sous formules équivalentes
Dans une formule, substituer une sous-formule par une autre revient à retirer toutes la partie de l’arbre qui descend d’un nœud et la remplacer par un autre sous-arbre.
Si la sous-formule “greffée” est équivalente à la sous-formule retirée, alors la nouvelle formule est équivalente à l’originale.
L’intérêt des substitutions est de simplifier la formule pour rendre son interprétation plus facile.
Une simplification forte (bien qu’elle agrandisse l’arbre) consiste à restreindre le nombre de symboles utilisés.
On peut ainsi toujours transformer une formule $\phi$ par une formule $\phi_{\neg,\lor,\land}\equiv\phi$ avec tous ses connecteurs logiques dans $\set{\neg,\lor,\land}$.
Il suffit en effet de substituer les nœuds $\rightarrow$ et $\leftrightarrow$ :
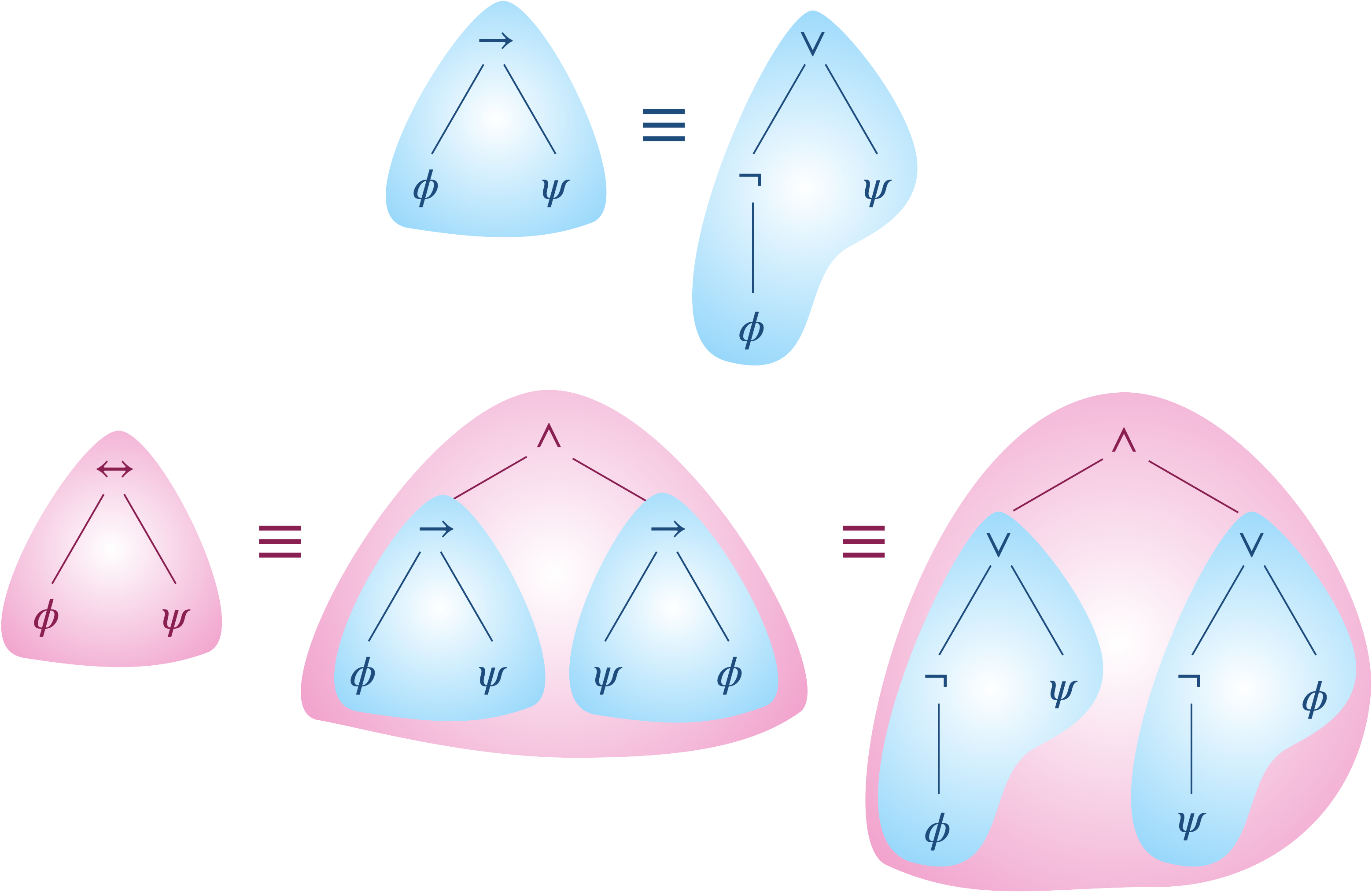
On peut aller encore plus loin en transformant une formule $\phi$ par une formule $\phi_{\neg,\lor}\equiv\phi$ avec tous ses connecteurs logiques dans $\set{\neg,\lor}$.
Ou bien en transformant une formule $\phi$ par une formule $\phi_{\neg,\land}\equiv\phi$ avec tous ses connecteurs logiques dans $\set{\neg,\land}$.
On utilise pour cela les deux substitutions suivantes :
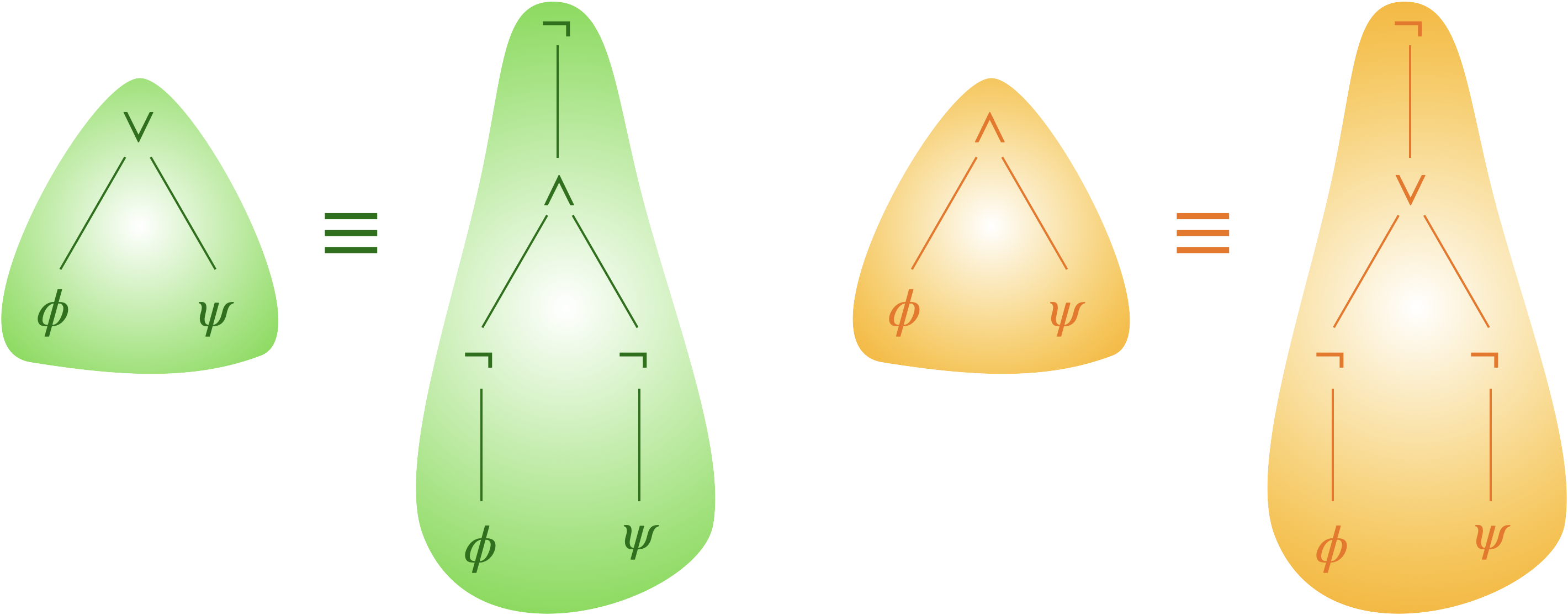
Dans l’exemple suivant, on détermine une formule équivalente avec $\neg$ et $\lor$ comme seuls connecteurs logiques (et on élimine les doubles négations dans la dernière étape.
Jeux d’évaluation
Ernst Zermelo a démontré que les jeux tour à tour à deux joueurs finis, à information parfaite (pas comme la bataille navale), sans hasard, et sans match nul, sont tous déterminés.
Cela signifie qu’un des deux joueurs a une stratégie gagnante.
Pour pouver ce résultat, on va représenter toutes les configurations possibles dans le jeu par un arbre dont les nœuds sont étiquetés par un des deux joueurs (0 ou 1) et les arêtes sont ses coups possibles depuis cette position. Les feuilles de l’arbre correspondent à des positions gagnantes, soit pour 0, soit pour 1. Puis on va décrire un algorithme permettant de déterminer lequel des deux joueurs a une stratégie gagnante sur une position donnée.
On commence par colorier en rouge les feuilles gagnantes pour 0 et en vert les feuilles gagnantes pour 1.
Ensuite on regarde les prédécesseurs de ces feuilles :
- s’il s’agit d’une position de 0, alors
- on le colorie en rouge si au moins un des successeurs est rouge car alors 0 peut y aller et gagner.
- on le colorie en vert si tous ses successeurs sont verts (car 0 n’a alors pas d’autre choix que d’aller sur une position gagnante de 1 et lui donner la victoire).
- s’il s’agit d’une position de 1, alors on inverse le raisonnement :
- on le colorie en vert si au moins un des successeurs est vert car alors 1 peut y aller et gagner.
- on le colorie en rouge si tous ses successeurs sont rouges (car 1 n’a alors pas d’autre choix que d’aller sur une position gagnante de 0 et lui donner la victoire).
On répète ensuite la procédure avec les prédécesseurs des nœuds que l’on vient de colorer jusqu’à remonter à la racine.
Comme on finira fatalement par colorier ainsi chaque nœud de l’arbre, on prouve qu’il existe au moins une stratégie gagnante pour chacun des sous-arbres et pour le jeu complet.
Un petit exemple :
Étant donné un modèle $\mathcal{M}$ et une formule $\phi \in \mathcal{F}$, la valeur que prend la formule dans le modèle peut être obtenue grâce à un jeu inventé par Jaakko Hintikka, noté $\mathbb{E}v(\mathcal{M},\phi)$ et appelé jeu d’évaluation.
$\phi$ doit être écrite avec seulement les connecteurs logiques $\neg$, $\land$ et $\lor$ (ce qui, comme on l’a vu, est toujours possible).
Les deux joueurs s’appellent le Vérificateur (V) dont le but est de prouver que la formule est satisfaite dans le modèle ($\mathcal{M}\models\phi$) et le Falsificateur (F) qui doit montrer que la formule est fausse ($\mathcal{M}\not\models\phi$).
L’arbre du jeu correspond à l’arbre de la formule. Si un nœud est une disjonction $\lor$, c’est au tour de V et si c’est une conjonction $\land$, c’est au tour de F. Si le nœud est une négation $\neg$, les deux joueurs échangent leur rôle. De plus, les propositions vraies correspondent à des positions gagnantes pour V et les propositions fausses sont gagnantes pour F.
Grâce à ces règles, on obtient le théorème suivant :
- $\mathcal{M}\models\phi$ ssi V a une stratégie gagnante dans $\mathbb{E}v(\mathcal{M},\phi)$.
- $\mathcal{M}\models\neg\phi$ ssi F a une stratégie gagnante dans $\mathbb{E}v(\mathcal{M},\phi)$.
Prouvons-le par induction sur la hauteur de la formule $\phi$ :
- hauteur $0$ : correspond à une formule $\phi$ réduite à une variable propositionnelle. On vérifie alors tout de suite 1. et 2..
- hauteur $n+1$ :
- si $\phi=\neg\psi$, alors l'hypothèse d'induction opère sur $\psi$.
Le jeu d'évaluation impliquant $\psi$ est le même que celui impliquant $\phi$ à un changement de rôle près. Si $\psi$ est vraie, alors V a une stratégie gagnante dans $\mathbb{E}v(\mathcal{M},\psi)$ (par hypothèse d'induction) et donc F a une stratégie gagnante dans $\mathbb{E}v(\mathcal{M},\phi)$ (par la règle de changement de rôle). Une $\phi$ fausse donne bien une stratégie gagnante pour F. Et inversement, une $\phi$ vraie donnera bien une stratégie gagnante pour V. - si $\phi=\psi_1\land\psi_2$, alors l'hypothèse d'induction opère sur $\psi_1$ et $\psi_2$.
Puisqu'on est sur un $\land$, les règles du jeu stipulent que c'est au tour de F de jouer.
$\phi$ vraie implique $\psi_1$ et $\psi_2$ vraie, ce qui donne une stratégie gagnante pour V puisque les deux branches sont gagnantes. Et à l'inverse, si $\phi$ est fausse, cela implique qu'au moins une des sous-formules soit fausse et donc que F dispose d'au moins une branche avec une stratégie gagnante ce qui assure que le nœud $\land$ est gagnant pour F. - si $\phi=\psi_1\lor\psi_2$, alors l'hypothèse d'induction opère sur $\psi_1$ et $\psi_2$.
C'est au tour de V de jouer d'après les règles. Il n'a besoin que d'une branche gagnante pour rendre le nœud victorieux. Or si $\phi$ est vraie, c'est bien le cas : au moins une des sous-formules est vraie et donc au moins une branche victorieuse s'ouvre à V.
Et une $\phi$ fausse implique que les deux sous-formules sont fausses aussi et donc victorieuses pour F, ce qui donne le nœud $\lor$ à F.
Exemple : considérons la formule $\bar{\phi}=\neg (( \neg( \neg P \land (( Q\land ( R \land \neg P )) \lor ( Q \land \neg P ))) \land ( P \land ( R \lor \neg R )) \lor ( ( R \land Q ) ))$ dont l’arbre est représenté ci-dessous. Et on se donne le modèle $\mathcal{M}\models P,Q,\neg R$
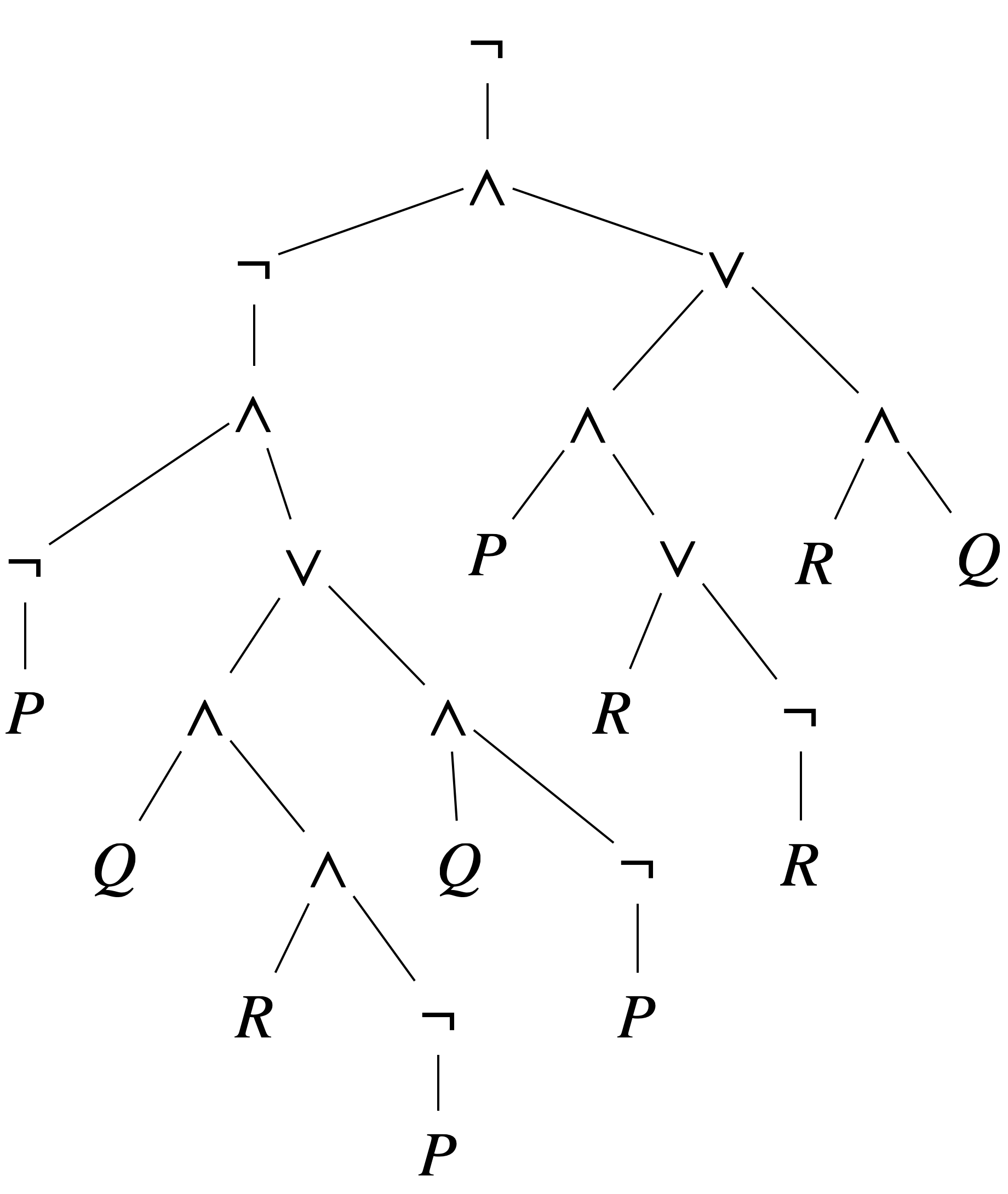
On commence par colorier les feuilles conformément au modèle, puis on remplace chaque occurrence de $\lor$, $\land$, $\neg$ respectivement par les symboles V, F et ⇔.
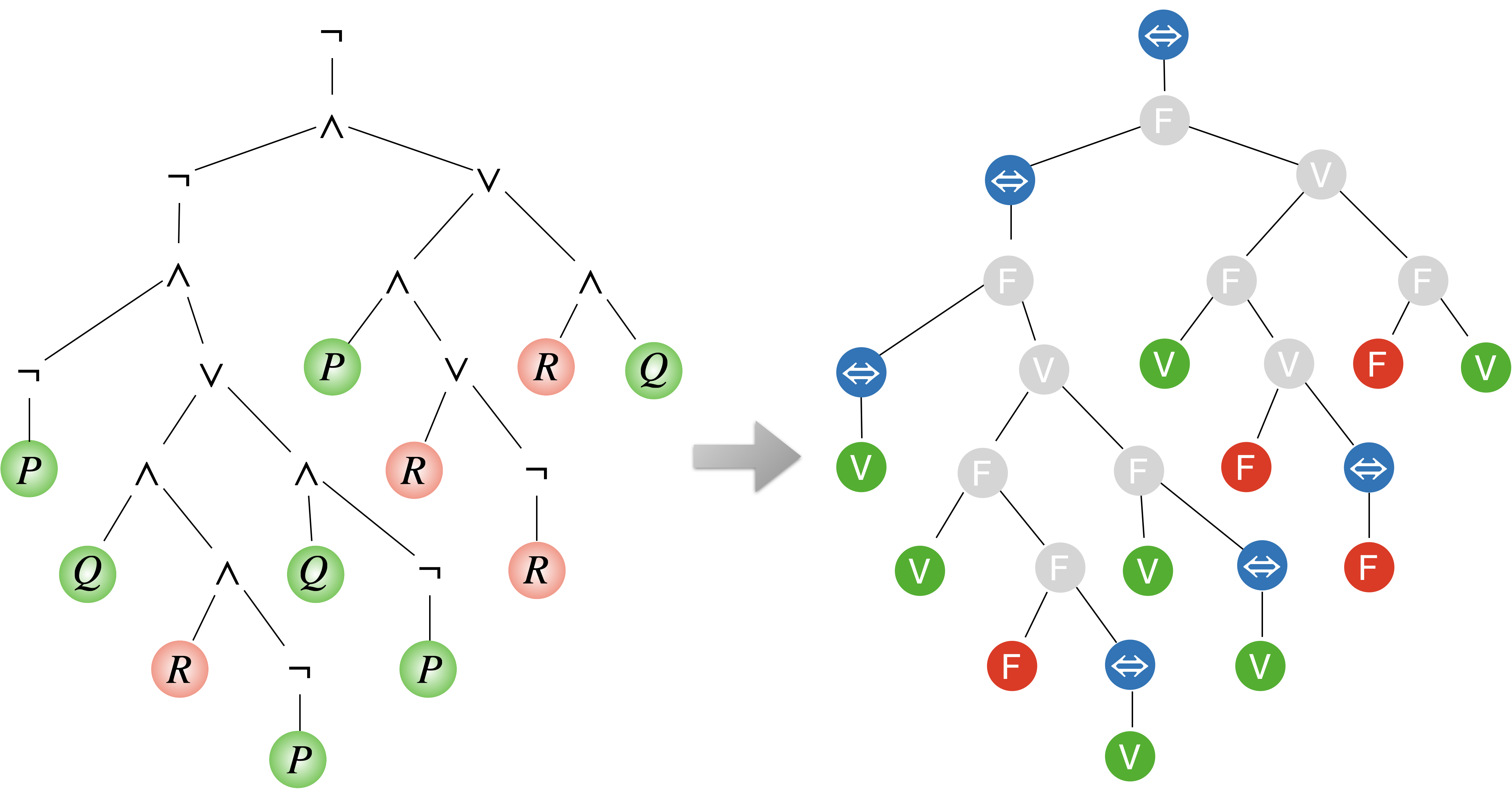
Ensuite on s’occupe des changements de rôle : si la branche connectant un nœud à la racine contient un nombre impair d’inversions, on intervertit l’étiquette du nœud, et sinon on la laisse telle quelle.
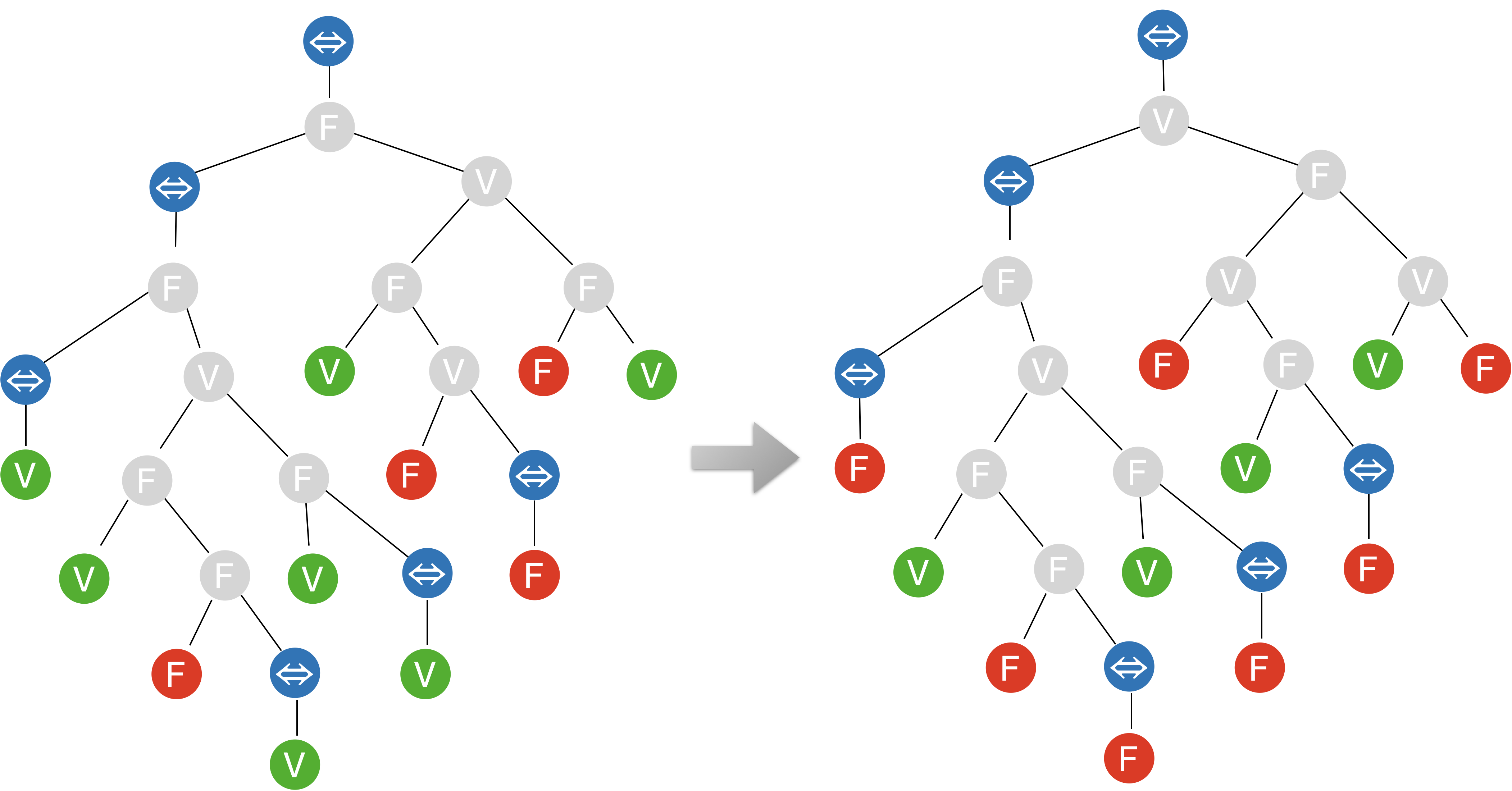
On peut maintenant retirer les symboles d’inversion et chercher lequel de V ou F a une stratégie gagnante en remontant depuis les feuilles.

Victoire au Falsificateur F ! D’après le théorème, on a donc $\mathcal{M}\not\models\phi$.
Les trois stratégies gagnantes possibles pour le Falsificateur sont les suivantes :
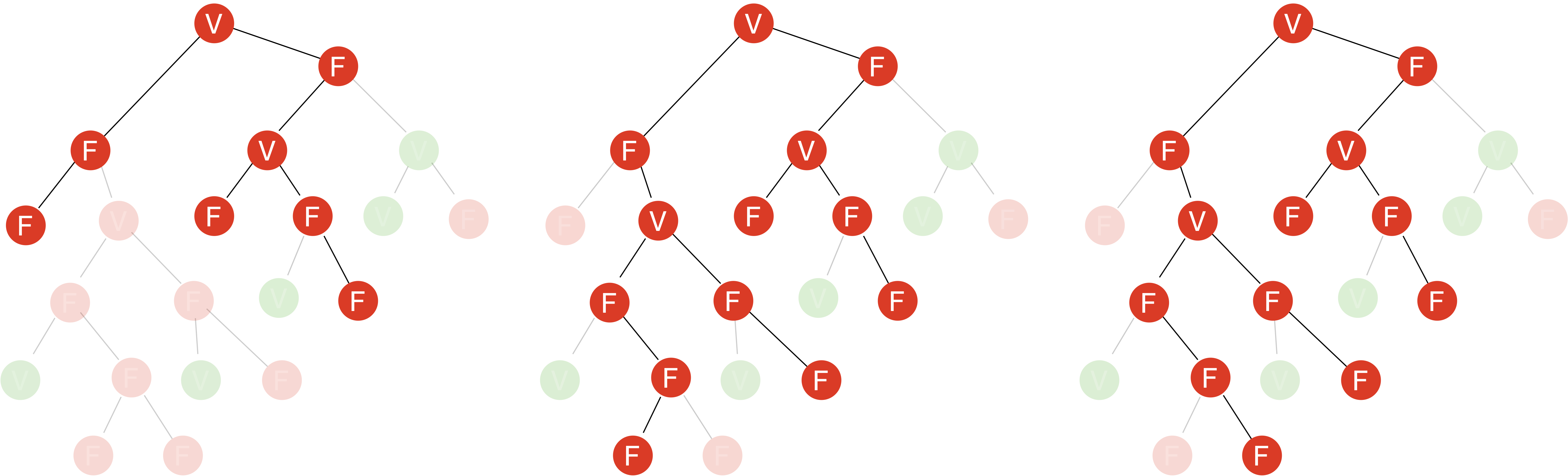
Table de vérité
Une table de vérité est un tableau regroupant de manière synthétique tous les modèles d’une fomrule donnée.
Si la formule possède $n$ variables propositionnelles, le tableau contient $2^n$ lignes, une ligne par modèle.
Exemple :
Construisons la table de vérité de $\phi := \left(\left(P\land\neg Q\right)\rightarrow\left(\neg\left( P\lor R\right) \leftrightarrow\neg Q\right)\right)$
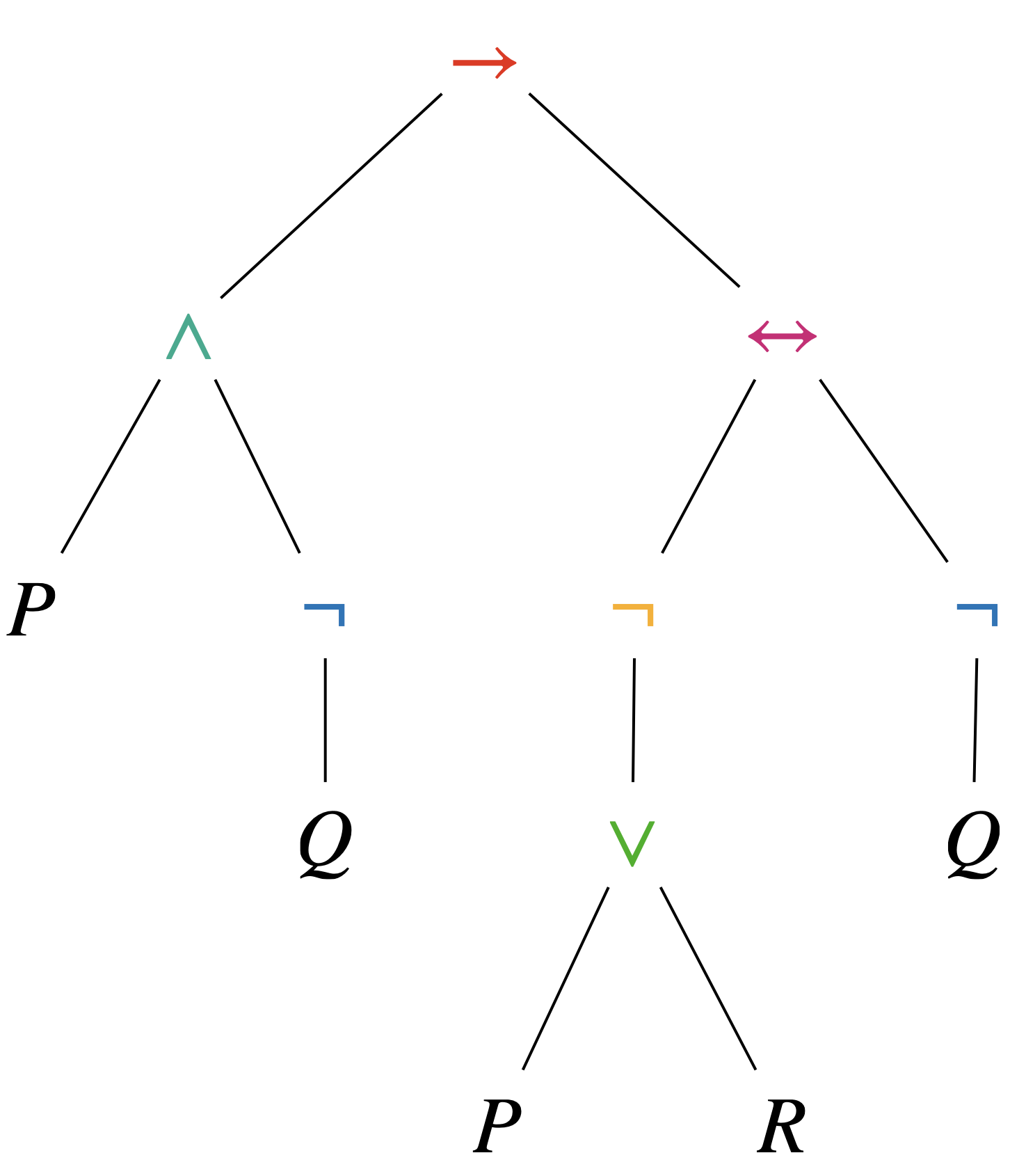

Tautologies et contradictions
On écrit alors aussi : $\phi \equiv \top$
Et rappelons le lien étroit entre la notion de tautologie et celle d’équivalence $\leftrightarrow$ :
Une contradiction est fausse dans tout modèle. Elle n’a donc pas de modèle ; une contradiction ne peut jamais avoir lieu.
Tautologies importantes :
| idempotence de la conjonction et de la disjonction | |
|---|---|
| $(P\land P)\leftrightarrow P$ | $(P\lor P)\leftrightarrow P$ |
| commutativité de la conjonction, disjonction et de la double implication | ||
|---|---|---|
| $(P\lor Q) \leftrightarrow (Q\lor P)$ | $(P\land Q) \leftrightarrow (Q\land P)$ | $(P\leftrightarrow Q) \leftrightarrow (Q\leftrightarrow P)$ |
| associativité de la disjonction, de la conjonction et de la double implication | ||
|---|---|---|
| $((P\lor Q) \lor R)\leftrightarrow (P\lor(Q\lor R))$ | $((P\land Q) \land R)\leftrightarrow (P\land(Q\land R))$ | $((P\leftrightarrow Q) \leftrightarrow R)\leftrightarrow (P\leftrightarrow(Q\leftrightarrow R))$ |
| distributivité de la disjonction par rapport à la conjonction et réciproquement | |
|---|---|
| $(P\lor (Q\land R))\leftrightarrow ((P\lor Q)\land (P\lor R))$ | $(P\land (Q\lor R))\leftrightarrow ((P\land Q)\lor (P\land R))$ |
| lois d'absorption | |
|---|---|
| $(P\land(P\lor Q))\leftrightarrow P$ | $(P\lor(P\land Q))\leftrightarrow P$ |
| lois de De Morgan | |
|---|---|
| $\neg (P\lor Q) \leftrightarrow (\neg P \land \neg Q)$ | $\neg (P\land Q) \leftrightarrow (\neg P \lor \neg Q)$ |
| contraposée |
|---|
| $(P\rightarrow Q) \leftrightarrow (\neg Q \rightarrow \neg P)$ |
Un raisonnement consiste généralement à partir d’une tautologie, la prémisse, et à aboutir à de nouvelles tautologies à partir d’implications (une tautologie étant vraie dans tout modèle, elle implique nécessairement une autre tautologie).
Dans un raisonnement par l’absurde (preuve par contradiction), pour montrer que $\phi$ est une tautologie, on suppose que $\neg \phi$ est vraie dans au moins un modèle pour aboutir à une contradiction $\psi$ ($\psi\equiv\bot$). Dans les modèles où $\neg \phi$ est vraie, $\neg \phi \rightarrow \psi$ est également vraie. Or $\neg\phi\rightarrow\psi\equiv \neg\neg\phi\lor\psi \equiv \phi\lor\bot \equiv \phi$. Donc dans les modèles où $\neg\phi$ est vraie, $\phi$ est vraie. Par conséquent, il n’y a pas de modèle où $\neg \phi$ est vraie. D’où $\phi\equiv\top$.
Formes normales
Supposons que l’on ait un nombre fini de variables propositionnelles $\set{P_1,P_2,\ldots,P_n}$.
On va construire une formule $\phi$ qui n’est vraie que dans un modèle $\mathcal{M}$ associé à une distribution de vérité $\delta$ :
$\displaystyle \phi = (\epsilon_1 P_1\land \epsilon_2 P_2\land\cdots\land\epsilon_n P_n) = \bigwedge_{i=1}^n \epsilon_i P_i$ où $\epsilon_i$ désigne $\neg$ si $\delta(P_i) = 0$ et $\not \! \neg$ si $\delta(P_i) = 1$ (avec $\not \! \neg P= P$).
La table de vérité aura bien des zéros partout sauf dans la ligne correspondant au modèle $\mathcal{M}$.
Passons maintenant d’une formule qui vérifie un seul modèle à une formule qui en vérifie plusieurs. Choisissons $\set{\mathcal{M}_i:i\in I}$ parmi les $2^n$ modèles possibles. En appelant $\phi$ la formule vraie dans $\mathcal{M}_i$, il suffit de former la formule suivante :
$\displaystyle \phi = \bigvee_{i\in I}\phi_i$
$\displaystyle \phi = \bigvee_{1≤i≤k} (\bigwedge_{1≤j≤n_i} \epsilon_{i,j}P_{i,j})$
On suppose ici que $\phi$ est satisfaite dans $k$ modèles, qu’un modèle $i$ parmi ces $k$ possède $n_i$ variables, et que pour une variable $P_{i,j}$ parmi ces $n_i$, $\epsilon_{i,j}$ désigne soit $\neg$, soit $\not\!\neg$.
Sinon, on construit $\phi$ à partir des modèles où elle est vraie comme expliqué plus haut.
$\displaystyle \phi = \bigwedge_{1≤i≤k} (\bigvee_{1≤j≤n_i} \epsilon_{i,j}P_{i,j})$
- Preuve sémantique :
- Ébauchons une preuve syntaxique (par un jeu de réécriture) :
- on commence par se débarrasser des connecteurs $\rightarrow$ et $\leftrightarrow$ pous n'avoir plus que $\lor$, $\land$ et $\neg$ et on se débarrasse des doubles négations,
- on utilise les lois de De Morgan pour faire entrer les négations à l'intérieur des formules jusqu'à ce que tous les symboles de négation soient placés devant une variable,
- on distribue la disjonction par rapport à la conjonction pour faire descendre les $\lor$ dans l'arbre de la formule jusqu'à ce qu'ils ne relient plus entre eux que des littéraux (des variables et leur négation).
On va construire une formule sur le modèle de celle ayant aboutit à la forme normale disjonctive mais on va maintenant supposer qu’on veut une formule $\psi$ qui soit vraie dans tout modèle à l’exception de certains.
Considérons $\set{\mathcal{M}_i: i\in I}$ l’ensemble des modèles dans lesquels $\phi$ est fausse. Si l’ensemble est vide, $\phi$ est une tautologie et $\psi=\bigwedge_{1≤i≤k} (\bigvee_{1≤j≤n_i} P_{i,j})$ marche. Sinon, considérons pour chaque $i$ dans $I$, la formule :
$ \begin{aligned} \psi_i &= \neg(\epsilon_1 P_1\land\epsilon_2 P_2 \land\cdots \land \epsilon_k P_k)\\ &= (\epsilon_1 \neg P_1\lor\epsilon_2 \neg P_2 \lor\cdots \lor \epsilon_k \neg P_k)\\ &= \bigvee_{1≤j≤k}\bar{\epsilon}_j P_j \end{aligned} $
Par construction, $\psi_i$ est vraie dans tous les modèles de $\phi$, à l'exception de $\mathcal{M}_i$. Ainsi la formule $\psi = \bigwedge_{i\in I}\psi_i$ est vraie dans tous les modèles possibles, à l'exception de tous les $\mathcal{M}_i$ pour $i$ dans $I$. $\psi$ est donc vraie dans tous les modèles de $\phi$ : $\mathcal{M}\models\phi$ ssi $\mathcal{M}\models\psi$, ce qui signifie bien que $\psi \equiv \phi$.
Exemple : Soit $\phi = \neg((\neg P \rightarrow Q)\rightarrow \neg (Q\leftrightarrow P))$$\begin{aligned} \phi &\equiv \neg ( \neg (\neg P \rightarrow Q ) \lor \neg ( Q \leftrightarrow P))\\ &\equiv \neg ( \neg ( \neg \neg P \lor Q ) \lor \neg ( Q \leftrightarrow P )\\ &\equiv \neg ( \neg (\neg\neg P\lor Q ) \lor \neg ( ( \neg Q \lor P ) \land ( \neg P \lor Q ) )\\ &\equiv \neg( \neg( P \lor Q ) \lor \neg ( ( \neg Q \lor P ) \land ( \neg P \lor Q ) )\\ &\equiv \neg \neg ( \lor Q ) \land \neg \neg ( ( \neg Q \lor P ) \land ( \neg P \lor Q ) ) \\ & \equiv ( P \lor Q ) \land ( ( \neg Q \lor P ) \land ( \neg P \lor Q ) ) \\ & \equiv ( P \lor Q ) \land ( \neg Q \lor P ) \land ( \neg P \lor Q ) \end{aligned} $
Et pour construire de la même manière une formule sous forme normale disjonctive, il suffit d’utiliser à la fin la distribution de la conjonction par rapport à la distribution puisqu’il s’agit cette fois-ci de faire descendre $\land$ dans l’arbre.
Sans stratégie, tester la validité d’une formule revient à vérifier sa véracité pour chaque combinaison des valeurs des variables, ce qui va dépendre exponentiellement du nombre de variables (ce qui devient vite impraticable). L’équivalence entre le tableau de vérité de la formule et sa forme normale conjonctive ($\phi=\bigwedge_{i}\phi_i$) permet un test syntaxique rapide de la validité. Pour vérifier que chaque $\phi_i$ est une tautologie, il suffit de s’assurer de la présence dans chaque $\phi_i=\bigvee_j P_j$ d’une couple contradictoire $P_j$ et $\neg P_j$.
Et pour un test de satisfabilité, la forme normale disjonctive $\phi=\bigvee_j \phi_i$ est plus adaptée. On va à nouveau tester la présence d’un couple de variables contradictoires dans les $\phi_i=\bigwedge_{j}P_j$. Si on revient bredouille pour au moins un $i$ alors la formule est satisfaisable.
Connecteurs binaires et systèmes complets de connecteurs
Appelons $*$ un connecteur binaire quelconque. On a 4 modèles possibles à considérer et comme la valeur de $P*Q$ dans chacun de ces modèles peut être soit vraie, soit fausse, cela fait en tout $4^2$ tables de vérité possibles et donc 16 connecteurs binaires différents :
| P | Q | $\bot$ | $\not \!\lor$ | $\not \! \leftarrow$ | $\not\!\pi_1$ | $\not \rightarrow$ | $\not\!\pi_2$ | $\not \! \leftrightarrow$ | $\not \!\!\land$ | $ \land$ | $ \leftrightarrow$ | $ \pi_2$ | $ \rightarrow$ | $ \pi_1$ | $ \leftarrow$ | $ \lor$ | $ \top$ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
On retrouve ainsi les 4 connecteurs binaires du calcul des propositions ($\lor$, $\land$, $\rightarrow$, $\leftrightarrow$) mais aussi le dual de chacun d’eux ($\not\!\lor$, $\not\!\!\land$, $\not\!\rightarrow$, $\not\!\leftrightarrow$) où $P\!\not \!* \;Q\equiv\neg(P*Q)$.
On trouve aussi l’implication inverse $\leftarrow$ et son dual $\not\!\leftarrow$, le connecteur $\top$ qui vaut toujours 1 et son dual $\bot$ qui vaut 0 dans tout modèle.
Et on découvre enfin deux connecteurs $\pi_1$ qui donne à la formule la valeur de $P$ et $\pi_2$ qui lui donne la valeur de $Q$ et leurs duaux $\not\!\pi_1$ et $\not\!\pi_2$ qui donnent respectivement $\neg P$ et $\neg Q$.
Chaque connecteur peut être exprimé par une formule du calcul des propositions (c.-à-d. qu’on peut les écrire à partir des 4 connecteurs binaires de base et la négation).
$P\not \! \lor \; Q \equiv \neg(P\lor Q)$
$P\not \! \rightarrow Q \equiv \neg(P\rightarrow Q)$
$P\!\not \! \pi_1 \;Q \equiv \neg P$
$P\,\not \! \leftarrow Q \equiv \neg(Q\rightarrow P)$
$P\!\not \! \pi_2 \;Q \equiv \neg Q$
$P\,\not \! \leftrightarrow Q \equiv \neg(P\leftrightarrow Q)$
$P\,\not \!\! \land \;\; Q \equiv \neg(P\land Q)$
$P \leftarrow Q \equiv Q \rightarrow P$
$P \; \top \; Q \equiv P \leftrightarrow P$
$P\; \pi_1 \;Q \equiv P$
$P\; \pi_2 \;Q \equiv Q$
On peut généraliser à des connecteurs d’arité quelconque. Toute formule $\gamma$ écrite avec ces connecteurs est équivalente à une formule du calcul des propositions.
Il suffit de trouver une formule $\phi$ qui ait les mêmes modèles que $\gamma$.
Imaginons par exemple que les variables propositionnelles de $\gamma$ soient $P_1$, $P_2$, $P_3$ et $P_4$ et supposons que dans un modèle $\mathcal{M}$ de $\gamma$, $P_3$ soit fausse et les autres vraies, alors la formule suivante sera vraie dans le modèle $\mathcal{M}$ et seulement dans lui : $\phi_\mathcal{M}=\left(P_1\land P_2 \land \neg P_3 \land P_4\right)$.
Construisons maintenant une formule $\phi$ vraie dans tous les modèles $\mathcal{M}_i$ tels que $\mathcal{M}_i \models \gamma$ en formant la disjonction des formules $\phi_{\mathcal{M}_i}$ : $\phi = \bigvee_{1≤i≤n}\phi_{\mathcal{M}_i}$.
$\phi$ est vraie dans un modèle possible de $\gamma$ si seulement si $\gamma$ est vraie dans ce modèle. On a donc bien $\phi\equiv\gamma$.
Un ensemble de connecteurs est appelé système complet de connecteurs si pour toute formule $\phi \in \mathcal{F}$, il existe une formule $\gamma$ écrite seulement avec ces connecteurs et telle que $\phi\equiv\psi$.
Ce système complet est dit minimal si tout ensemble plus petit de connecteurs n'est pas complet.
On a déjà montré que toute formule du calcul des propositions peut s’écrire avec uniquement les connecteurs $\set{\neg,\lor\land\rightarrow,\leftrightarrow}$ et plus avant, on a vu qu’on pouvait écrire les autres connecteurs à partir de $\set{\neg,\lor}$ ou de $\set{\neg,\land}$.
On voit tout de suite que $\set{\neg,\lor,\land\rightarrow,\leftrightarrow}$ n’est pas minimal mais qu’en est-il pour les deux autres ?
Prouvons-le pour $\set{\neg,\lor}$ (il suffit d'intervertir $\lor$ et $\land$ pour obtenir l'autre preuve) en considérant toutes les réductions de l'ensemble possibles :
- $\set{}$ : les formules ne sont plus que des variables propositionnelles. Or une variable propositionnelle $R$ ne peut pas être équivalente à une formule comme $P\lor Q$. Raisonnons par l'absurde en supposant que $R\equiv P\lor Q$ :
- si $R=P$, on considère le modèle dans lequel $P$ est fausse et $Q$ est vraie pour aboutir à une contradiction.
- si $R=Q$, on considère le modèle dans lequel $Q$ est fausse et $P$ est vraie pour aboutir à une contradiction.
- si $R\not = P,Q$, on considère n'importe quel modèle où $R$ est fausse et $P$ est vraie pour aboutir à une contradiction.
- $\set{\neg}$ : dans ce cas les formules s'écrivent $\neg\cdots\neg R $. Si elle contient un nombre pair de négations, on retombe sur le cas précédent, sinon il suffit de trouver une formule du calcul des propositions qui ne puisse pas être équivalente à $\neg R$. Et $P\lor Q$ convient à nouveau. Raisonnons par l'absurde en supposant que $\neg R\equiv P\lor Q$ : :
- si $R=P$, il suffit d'un modèle où $P$ est vraie pour aboutir à une contradiction.
- si $R=Q$, il suffit d'un modèle où $Q$ est vraie pour aboutir à une contradiction.
- si $R\not = P,Q$, il suffit d'un modèle où $R$ et $P$ sont vraies pour aboutir à une contradiction.
- $\set{\lor}$ : montrons qu'on ne peut pas créer de formule équivalente à $\neg P$ avec ce connecteur.
Toutes les formules construisibles sont dans ce cas de la forme $(P_1\lor\cdots\lor P_k)$.
Raisonnons par l'absurde en supposant que $(P_1\lor\cdots\lor P_k)\equiv \neg P$
Il suffit de considérer le modèle où tous les $P_i$ et $P$ sont vraies pour aboutir à une contradiction.
On peut faire encore mieux avec un système minimal ne contenant qu’un seul connecteur :
On note parfois $\not\!\lor$ avec une flèche vers le bas $\downarrow$, appelée flèche de Peirce, et $\not\!\!\land$ avec une flèche vers le haut $\uparrow$ ou une barre $\mid$, appelée barre de Sheffer.
Prouvons que $\set{\not\!\lor}$ est un système minimal complet :
Le caractère minimal ne faisant pas de doute, il suffit de montrer que $\set{\not\!\lor}$ est complet, c.-à-d. que pour toute formule $\phi \in \mathcal{F}$, il existe une formule équivalente $\psi$ écrite seulement avec $\not\!\lor$.
On va supposer que la formule $\phi$ ne contient que des négations et des disjonctions ($\set{\neg,\lor}$ est complet...) et on va raisonner par induction sur la hauteur de la formule :
- Si $\phi$ est de hauteur 0, alors $\phi=P$ et la formule $(P\not\!\lor \;P)\not\!\lor \;(P\not\!\lor \;P)$ convient puisque :
$ \begin{aligned} (P\not\!\lor \;P)\not\!\lor\;(P\not\!\lor \;P) &\equiv \neg((P\not\!\lor \;P)\lor(P \not\!\lor \;P)\\ &\equiv \neg (P \not\!\lor \;P)\\ &\equiv \neg\neg(P\lor P)\\ &\equiv \neg\neg P\\ &\equiv P \end{aligned} $
- On suppose maintenant que toutes les formules de hauteur $n$ peuvent s'écrire seulement avec $\not\!\lor$ et on vérifie que c'est encore le cas pour les formules de hauteur $n+1$. Comme $\phi$ ne contient que $\neg$ et $\lor$, seuls deux cas se présentent :
- $\phi=\neg\varphi$ : par hypothèse d'induction, $\varphi$ est équivalente à une formule $\psi'$ qui ne s'écrit qu'avec $\not\!\lor$. La formule $\psi=\psi' \not\!\lor \; \psi'$ convient :
$ \begin{aligned} \psi’ \not\!\lor \; \psi’ &\equiv \neg(\psi’\lor \psi’)\\ &\equiv \neg \psi’\\ &\equiv \neg \varphi\\ &\equiv \phi\\ \end{aligned} $
- $\phi=\phi_1\lor \phi_2$ : par hypothèse d'induction, $\phi_1$ et $\phi_2$ sont équivalentes respectivement à $\psi_1$ et $\psi_2$ qui ne s'écrivent qu'avec $\not\!\lor$. La formule $(\psi_1 \not\!\lor \; \psi_2)\not\!\lor \; (\psi_1 \not\!\lor \;\psi_2)$ convient :
$ \begin{aligned} (\psi_1 \not\!\lor \; \psi_2)\not\!\lor \;(\psi_1 \not\!\lor \;\psi_2) &\equiv \neg((\psi_1 \not\!\lor \;\psi_2)\lor(\psi_1 \not\!\lor \;\psi_2)\\ &\equiv \neg (\psi_1 \not\!\lor \;\psi_2)\\ &\equiv \neg\neg(\psi_1\lor \psi_2)\\ &\equiv \psi_1\lor\psi_2\\ &\equiv \phi_1\lor\phi_2\\ &\equiv \phi \end{aligned} $
- $\phi=\neg\varphi$ : par hypothèse d'induction, $\varphi$ est équivalente à une formule $\psi'$ qui ne s'écrit qu'avec $\not\!\lor$. La formule $\psi=\psi' \not\!\lor \; \psi'$ convient :
C’est ainsi qu’un ordinateur peut être construit entièrement avec des portes logiques NAND ou NOR qui sont dites universelles (il semblerait que l’Apollo Guidance Computer qui servit à poser l’homme sur la Lune pendant le programme Apollo était construit exclusivement avec des portes NOR). Ces portes réalisent en effet électroniquement les opérations logiques $\not\!\!\land$ et $\not\!\lor$ et permettent donc de construire toutes les formules de la logique des propositions.

Après la notion de modèle, on va maintenant s’intéresser à la notion de preuve. Et ces deux notions seront réunies par le théorème de complétude.